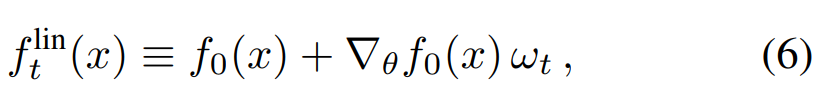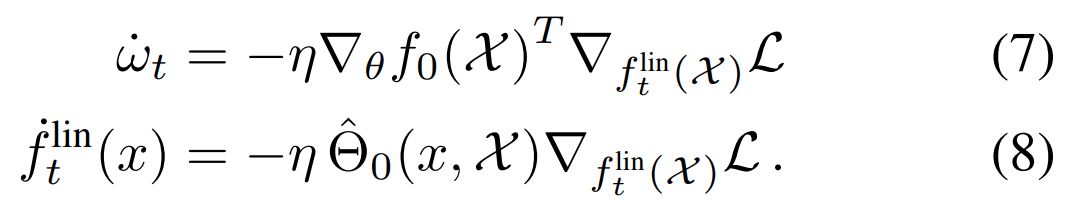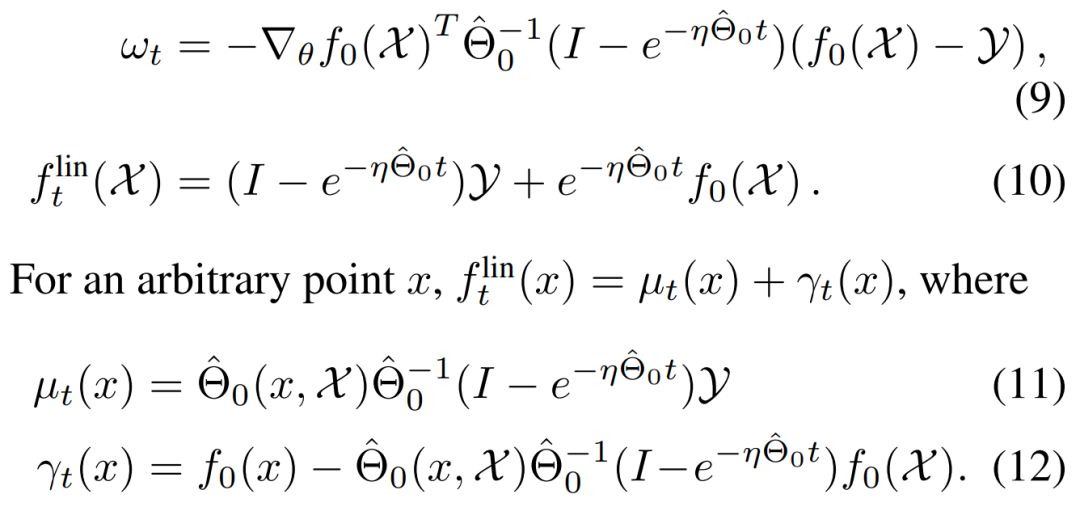谷歌大脑：只要网络足够宽，激活函数皆可抛

| 全文共3089字，建议阅读时6分钟 |

 

本文经机器之心（微信公众号：almosthuman2014）授权转载，禁止二次转载

选自：arXiv

作者：Jaehoon Lee 等

深度神经网络以其强大的非线性能力为傲，借助它可以拟合图像和语音等复杂数据。但最近谷歌大脑的研究者表明只要网络足够宽，线性化的网络可以产生和原版网络相近的预测结果和准确率，即使没有激活函数也一样。这有点反直觉，你现在告诉我 Wide ResNet 那样的强大模型，在 SGD 中用不用激活函数都一样？

 

基于深度神经网络的机器学习模型在很多任务上达到了前所未有的性能。这些模型一般被视为复杂的系统，很难进行理论分析。此外，由于主导最优化过程的通常是高维非凸损失曲面，因此要描述这些模型在训练中的梯度动态变化非常具有挑战性。

就像在物理学中常见的那样，探索此类系统的理想极限有助于解决这些困难问题。对于神经网络来说，其中一个理想极限就是无限宽度（infinite width），即全连接层中的隐藏单元数，或者卷积层中的通道数无穷大。在这种限制之下，网络初始化时的输出来自于高斯过程（GP）；此外，在使用平方损失进行精确贝叶斯训练后，网络输出仍然由 GP 控制。除了理论上比较简单之外，无限宽度的极限也具有实际意义，因为研究者发现更宽的网络可以更好地泛化。

谷歌大脑的这项研究探索了宽神经网络在梯度下降时的学习动态，他们发现这一动态过程的权重空间描述可以变得非常简单：随着宽度变大，神经网络在初始化时可以被其参数的一阶泰勒展开式（Taylor expansion）有效地代替。这样我们就可以得到一种线性模型，它的梯度下降过程变得易于分析。虽然线性化只在无限宽度限制下是精确的，但即使在有限宽度的情况下，研究者仍然发现原始网络的预测与线性化版本的预测非常一致。这种一致性在不同架构、优化方法和损失函数之间持续存在。

对于平方损失，精确的学习动态过程允许存在一个闭式解，它允许我们用 GP 来表征预测分布的演变。这个结果可以看成是「sample-then-optimize」后验采样向深度神经网络训练的延伸。实验模拟证实，对于具有不同随机初始化的有限宽度模型集合，实验结果可以准确地建模了其预测的变化。

论文的主要贡献：

作者表明，这项研究工作最重要的贡献是展示了参数空间中的动态更新过程等价于模型的训练动态过程（dynamics），且该模型是网络所有参数（权重项与偏置项）的仿射变换。无论选择哪种损失函数，该结果都成立。尤其是在使用平方损失时，动态过程允许使用闭式解作为训练时间的函数。所以像 Wide ResNet 那样的强大非线性模型，只要足够宽，它可以直接通过线性的仿射变换直接模拟，激活函数什么的都没啥必要了～

这些理论可能看起来太简单了，不适用于实践中的神经网络。尽管如此，作者仍然通过实验研究了该理论在有限宽度中的适用性，并发现有限宽度线性网络能表征各种条件下的学习动态过程和后验函数分布，包括表征实践中常用的 Wide ResNet。

论文：Wide Neural Networks of Any Depth Evolve as Linear Models Under Gradient Descent

论文链接：https://arxiv.org/pdf/1902.06720.pdf

摘要：深度学习研究的长期目标是准确描述训练和泛化过程。但是，神经网络极其复杂的损失函数表面使动态过程的理论分析扑朔迷离。谷歌大脑的这项研究展示了，宽神经网络的学习动态过程难度得到了极大简化；而对于宽度有限的神经网络，它们受到线性模型的支配，该线性模型通过初始参数附近的一阶泰勒展开式进行定义。此外，具备平方损失的宽神经网络基于梯度的训练反映了宽贝叶斯神经网络和高斯过程之间的对应，这种宽神经网络生成的测试集预测来自具备特定组合核（compositional kernel）的高斯过程。尽管这些理论结果仅适用于无限宽度的神经网络，但研究者找到了一些实验证据，证明即使是宽度有限的现实网络，其原始网络的预测结果和线性版本的预测结果也符合该理论。这一理论在不同架构、优化方法和损失函数上具备稳健性。

理论结果

线性化网络

在实验部分，本论文展示了线性化网络（linearized network）能获得和原始深度非线性网络相同的输出结果和准确率等。这一部分简单介绍了什么是线性化的网络，更多理论分析可以查看原论文的第二章节。对于线性化网络的训练动态过程，首先我们需要将神经网络的输出替换为一阶泰勒展开式：

其中 ω_t ≡ θ_t − θ_0 表示模型参数从初始值到终值的变化。表达式 (6) 左边的 f_t 为两项之和：第一项为网络的初始化输出，根据泰勒公式，它在训练过程中是不改变的；第二项则会捕捉初始值在训练过程中的变化。如果我们使用线性函数，那么梯度流的动态过程可以表示为：

因为 f_0 对θ的梯度 ∇f_0 在整个训练中都为常数，这些动态过程会显得比较简单。在使用 MSE 损失函数时，常微分方程有闭式解：

因此，尽管没有训练该网络，我们同样能获得线性化神经网络沿时间的演化过程。我们只需要计算正切核函数 Θ_0 hat 和初始状态的输出 f_0，并根据方程 11、12 和 9 计算模型输出和权重的动态变化过程。重要的是，这样计算出来的值竟然和对应非线性深度网络迭代学习出来的值非常相似。

实验

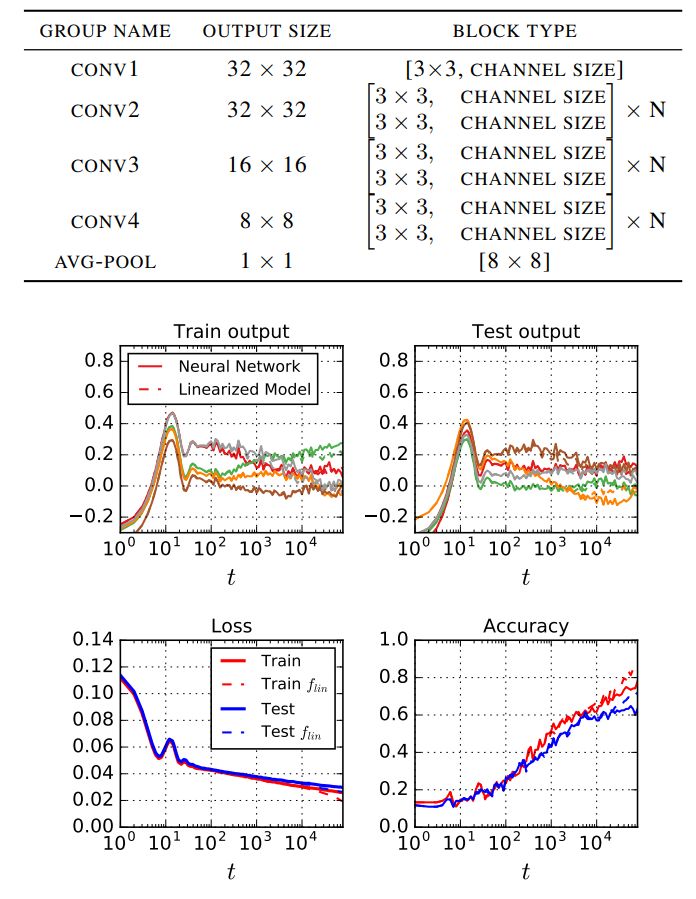
本研究进行了实验，以证明宽神经网络的训练动态能够被线性模型很好地捕捉。实验包括使用全批量和小批量梯度下降的全连接、卷积和 wide ResNet 架构（梯度下降的学习率非常小），以使连续时间逼近（continuous time approximation）能够发挥作用。实验考虑在 CIFAR10 数据集上进行二分类（马和飞机）、在 MNIST 和 CIFAR-10 数据集上进行十个类别的分类。在使用 MSE 损失时，研究者将二分类任务作为回归任务来看待，一个类别的回归值是+1，另一个类别的回归值是-1。

原始网络与线性网络之间的训练动态过程对比

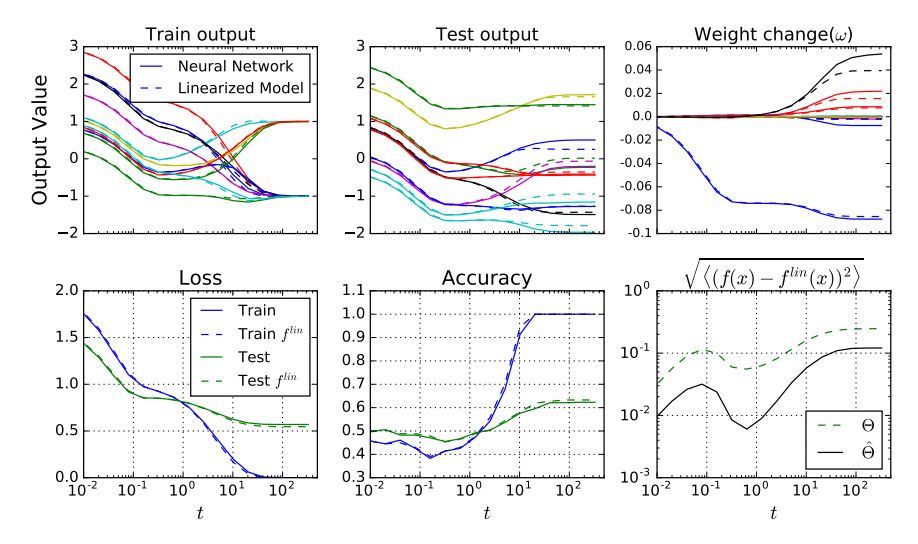
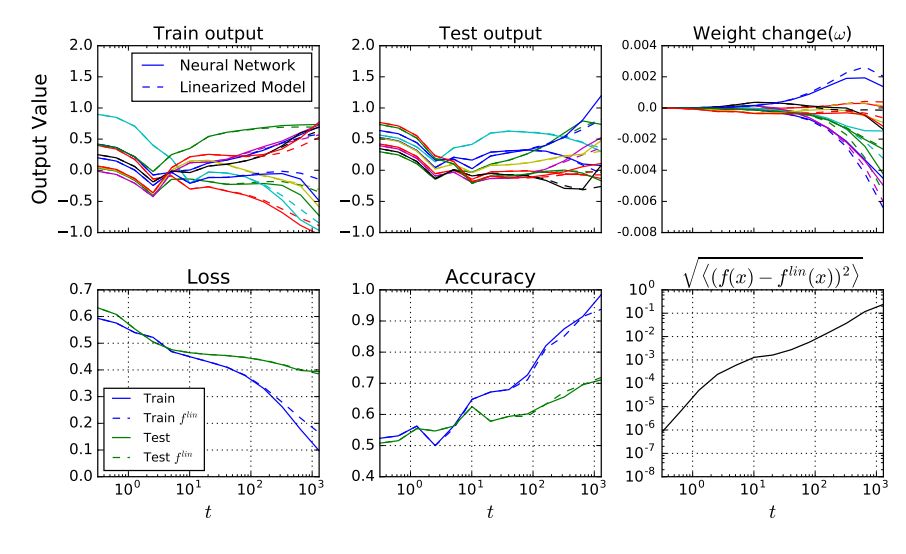
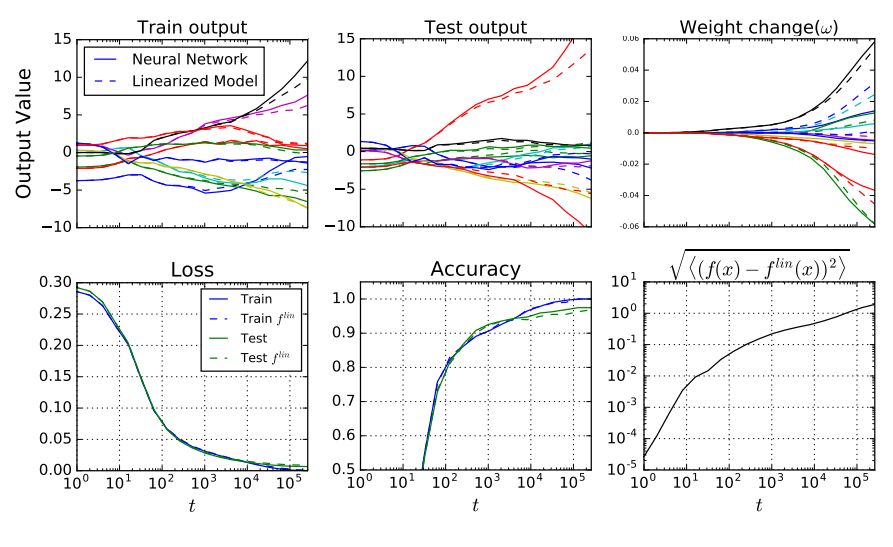
图 5、6、7 对比了线性网络和实际网络的训练动态过程。所有示例中二者都达到了很好的一致。

图 4 展示了线性模型可以很好地描述在 CIFAR-10 数据集上使用交叉熵损失执行分类任务时的学习动态。图 6 使用交叉熵损失测试 MNIST 分类任务，且使用动量法优化器进行训练。图 5 和图 7 对比了对线性网络和原始网络直接进行训练时二者的训练动态过程。

图 4：在模型上执行全批量梯度下降与线性版本上的分析动态过程（analytic dynamics）类似，不管是网络输出，还是单个权重。

图 5：使用具备带有动量的最优化器进行全批量梯度下降时，卷积网络和其线性版本的表现类似。

图 6：神经网络及其线性版本在 MNIST 数据集上通过具备动量的 SGD 和交叉熵损失进行训练时，表现类似。

图 7 对比了使用 MSE 损失和具备动量的 SGD 训练的 Wide ResNet 的线性动态过程和真实动态过程。研究者稍微修改了图 7 中的残差模块结构，使每一层的通道数保持固定（该示例中通道数为 1024），其他与原始实现一致。

图 7：Wide ResNet 及其线性化版本表现类似，二者都是通过带有动量的 SGD 和 MSE 损失在 CIFAR-10 数据集上训练的。

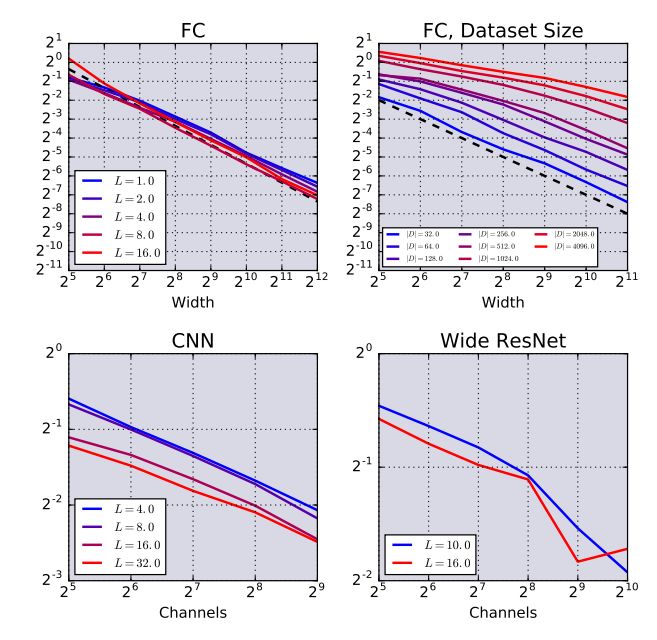
图 8 为一系列模型绘制了平台均方根误差（plateau RMSE），它是宽度和数据集大小的函数。总体来看，误差随宽度的增加而降低。全连接网络的误差降幅约为 1/N，卷积和 WRN 架构的误差降幅更加模糊。

图 8：误差取决于深度和数据集大小。

新维空间站相关业务联系：

刘老师 13901311878

孙老师 17316022016

邓老师 17801126118

微信公众号又双叒叕改版啦

快把“MOOC”设为星标

不错过每日好文☟

喜欢我们就多一次点赞多一次分享吧~

有缘的人终会相聚，慕客君想了想，要是不分享出来，怕我们会擦肩而过~

《预约、体验——新维空间站》

《【会员招募】“新维空间站”1年100场活动等你来加入》

《有缘的人总会相聚——MOOC公号招募长期合作者》

产权及免责声明

本文系“MOOC”公号转载、编辑的文章，编辑后增加的插图均来自于互联网，对文中观点保持中立，对所包含内容的准确性、可靠性或者完整性不提供任何明示或暗示的保证，不对文章观点负责，仅作分享之用，文章版权及插图属于原作者。如果分享内容侵犯您的版权或者非授权发布，请及时与我们联系，我们会及时内审核处理。

了解在线教育，
把握MOOC国际发展前沿，请关注：
微信公号：openonline
公号昵称：MOOC