“德州扑克AI之父”再发新论文:“冷扑大师2.0”要来了?
来源:arXix,新智元
最近,Arxiv上的一篇题为《Solving Imperfect-Information Games via Discounted Regret Minimization》引发关注,原因主要在于本文的两位作者的鼎鼎大名,CMU计算机系博士生Noam Brown,以及该校计算机系教授Tuomas Sandholm。这两位就是去年的著名的德州扑克AI程序“冷扑大师”(Libratus)的缔造者,堪称德州扑克AI之父。
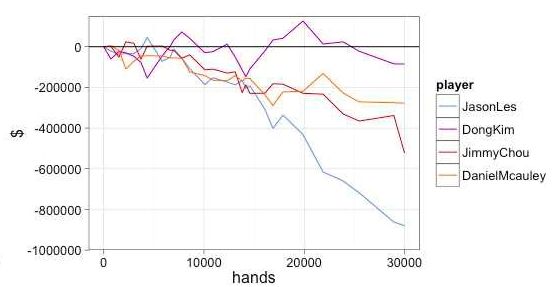
“冷扑大师”在去年曾与4位人类专业德州扑克牌手大战20天,最后全面获胜。两位作者还去Reddit论坛的机器学习板块上搞了一次“Ask me anything”的网友问答互动,一时名声大噪。阐述“冷扑大师”背景技术的论文也被评为NIPS 2017最佳论文。
“冷扑大师”在2017年的人机德州扑克大赛面对4位专业人类牌手,全部获胜
时隔一年多,二位大师再次发布关于不完全信息博弈策略的论文,仍主要以德州扑克为测试基准平台,难道“冷扑大师”2.0就要来了?人类牌手们,准备好(再次)被碾压了吗?
一起看看这篇文章都讲了些什么。
论文地址:
https://arxiv.org/abs/1809.04040
Counterfactual regret minimization(CFR)是目前很流行的一系列迭代算法,实际上也是近似解决大型不完美信息游戏的最快的AI算法。本算法系列中提出了一个“后悔值” (regrets)的概念,即在当前状态下,选择行为A,而不是行为B,后悔的值是多少。
在本文中,我们介绍了一些CFR算法的一些新变化,其中包括1)采用多种方法从早期迭代中减低“后悔值”(regret)(在某些情况下对正面和负面后悔值使用不同策略)。(2)以各种方式对迭代进行重新加权,以获得更佳的输出策略。(3)使用非标准化的后悔值最小化策略。(4)利用optimistic regret matching。这些方法可以在诸多环境中显著提高性能。
首先,我们在每个测试的游戏中引入一个优化的CFR +的变体算法,这是之前最先进的算法。CFR+是一个强大的基准,没有其他算法能够超越它。我们表明,与CFR +不同,许多基于CFR的重要的新算法与现代不完全信息游戏修剪技术兼容,而且与游戏树中的样本兼容。
不完全信息博弈模拟互相拥有隐藏信息的玩家之间的战略互搏,比如谈判、网络安全和拍卖都是属于此类。扑克游戏是这类博弈的常用测试基准。
这种测试的一般目标是找到一种(近似的)均衡,在这种均衡状态下,没有玩家可以通过偏离该均衡状态来提高自己的收益。对于线性程序无法应对的的极大规模的不完全信息博弈,通常使用迭代算法来近似均衡。
CFR方法的主要思想是把游戏中所有状态都考虑到,生成一颗完整的状态树。对树的每一个节点都初始化一个策略,然后根据这个策略来玩游戏。每次都走状态树的一条边,然后根据游戏的结果来更新相关节点的策略。
当CFR进行了许多次迭代之后,这个状态树的每条路径都被遍历了很多次,每个节点的策略都被更新趋于均衡了,从而得到一个可以玩游戏的AI。
德州扑克是测试不完全信息博弈算法表现的典型游戏。在本文中使用无限制Heads-up德州扑克规则。两位玩家(P1和P2)起手筹码各为20000美元,大/小盲注为50/100美元。每轮加注不得少于100美元。让对方筹码降至0者获胜。
除了德州扑克外,本文采用了另一种纸牌游戏Goofspiel,两位玩家各拥有5张手牌(A、2、3、4、5),牌桌中间有5张牌的奖励牌堆,牌堆中的牌也是A\2\3\4\5。每轮从牌堆中先翻开最上面的牌作为奖励牌,然后两名牌手同时出一张手牌比大小,胜者赢得奖励牌,用过的手牌被弃掉。最后以奖励牌总分数(A为1分、2为2分,以此类推)多者获胜。
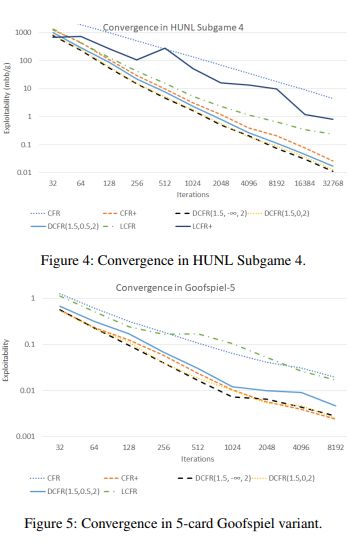
我们的实验针对德州扑克进行了32768次迭代,对Goofspiel进行了8192次迭代。由于是近似均衡,而不是精确均衡,所以何时终止迭代计算很大程度上取决于实验者,一般取100-1000次迭代的结果就是有意义的。
所有实验都使用CFR的交替更新形式。我们衡量两个玩家的平均可利用性。我们的实验表明,在某些游戏中,线性CFR(LCFR)可以在合理的时间范围内显着提高CFR +的性能。
然而,LCFR在实际实验中的表现似乎比CFR+差。线性CFR在Subgame1和3中的表现特别好,与Subgame2和4相比,相对于每个玩家可以下注的最高金额,底池中筹码价值很小,这时更容易出现严重的错误行为。在Goofspiel中,线性CFR同样表现不佳,这表明线性CFR特别适合可能出现严重错误的游戏。
NormalHedge CFR(NH)是一个在游戏中每个信息集中独立应用regret最小化的框架。通常,我们使用Regret Matching(RM)作为实现后悔最小化的工具,主要是由于无参数的特点和简单的实现形式。但是,我们也可以应用任何其他实现regret最小化的工具。
我们使用Normal Hedge(NH)作为CFR中的regret最小化工具进行研究。
NH与RM都具备两个很理想的特点:都没有任何参数,并且会向后悔值为负的行为分配“零概率”(这意味着它可以很容易地用于CFR +上)。不过,NH操作在计算上比RM成本更高,因为它涉及取幂和线搜索。
我们发现,NH在具有大错误动作的游戏中可能做得更好。在这些实验中,NH的性能是根据可利用性作为迭代次数的函数来测量的。但是,在我们的实现中,由于NH中涉及取幂和行搜索操作,每次迭代所需的时间要比RM方法长五倍。
因此,使用NH实际上减慢了实践中的收敛。然而,在指数和线搜索操作的成本无关紧要的某些情况下,比如算法的瓶颈主要在于内存不足,而不是计算速度时,NH方法可能是更好的选择。
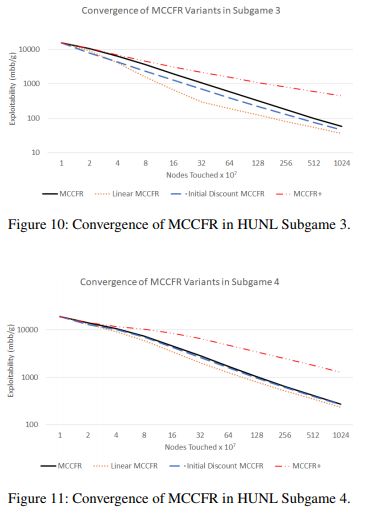
蒙特卡洛CFR(MCCFR)是CFR算法的另一变体,该算法对玩家的某些行为或机会结果进行采样。).
MCCFR与抽象方法相结合,可以产生最先进的面向德州扑克游戏的AI算法。该模型在没有特殊结构的博弈中特别有用,可以利用该算法来达成CFR的快速矢量实现。
MCCFR的种类不少,具有不同的采样方案。最流行的是外部采样MCCFR,其中根据其概率对对手和机会动作进行采样,但是遍历了更新regret值的玩家的所有行动。目前也存在其他性能优异的MCCFR变体,但外部采样式MCCFR简单且广泛使用,可用作我们实验的基准。
尽管CFR+在非抽样的情况下体现出比CFR更大的性能改进,但CFR+中的变化,在应用于MCCFR时并不会带来更优秀的性能。
上图表明,与vanilla MCCFR相比,模型在德州扑克上具有更优越的表现。在子游戏3(图中上半部分)中,这种性能提升尤为明显。
我们在本文中介绍了CFR算法的变体,可以对先前的迭代进行discount,并表现出比之前最先进的CFR +类算法更强大的性能,在涉及重大错误的环境中表现的更加明显。
论文地址:
Solving Imperfect-Information Games via Discounted Regret Minimization
https://arxiv.org/abs/1809.04040
广告 & 商务合作请加微信:kellyhyw
投稿请发送至:mary.hu@aisdk.com