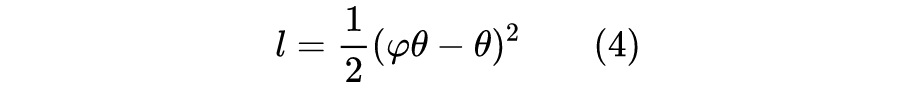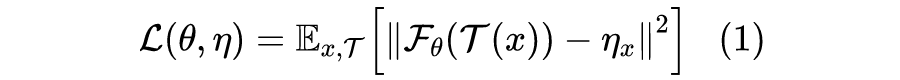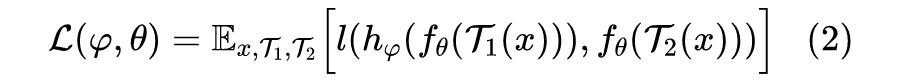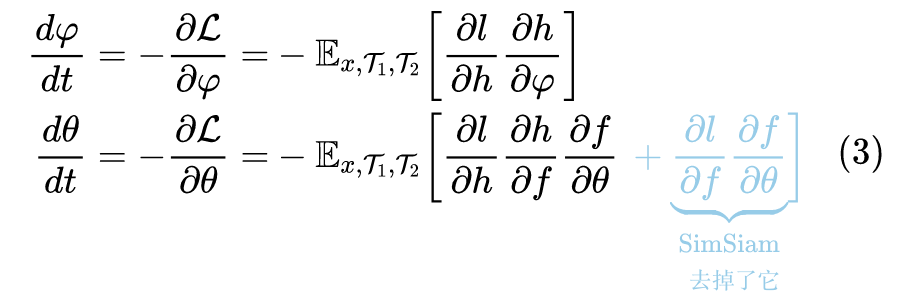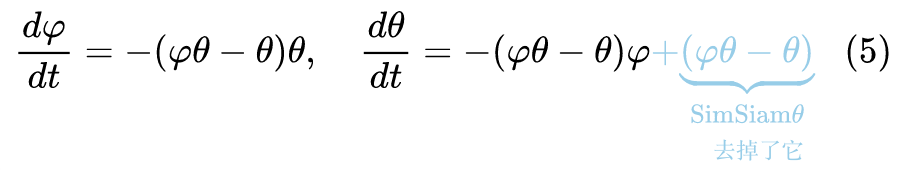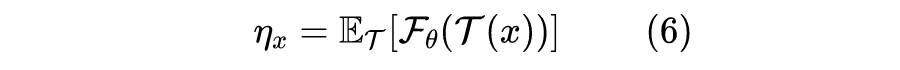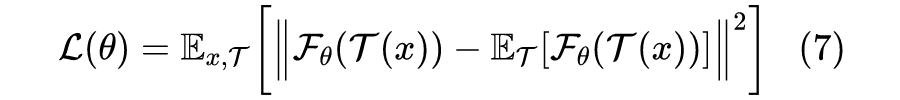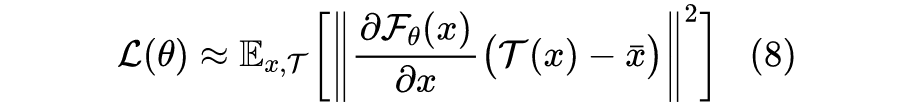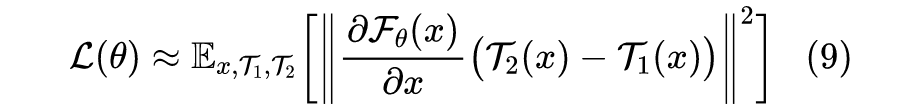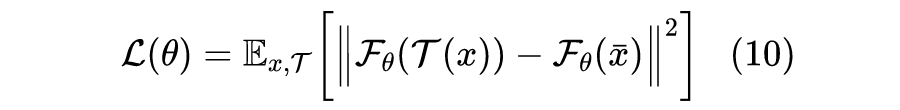从动力学角度看优化算法：为什么SimSiam不退化？

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

自 SimCLR [1] 以来，CV 中关于无监督特征学习的工作层出不穷，让人眼花缭乱。这些工作大多数都是基于对比学习的，即通过适当的方式构造正负样本进行分类学习的。

然而，在众多类似的工作中总有一些特立独行的研究，比如 Google 的 BYOL [2] 和最近的 SimSiam [3]，它们提出了单靠正样本就可以完成特征学习的方案，让人觉得耳目一新。但是没有负样本的支撑，模型怎么不会退化（坍缩）为一个没有意义的常数模型呢？这便是这两篇论文最值得让人思考和回味的问题了。

其中 SimSiam 给出了让很多人都点赞的答案，但笔者觉得 SimSiam 也只是把问题换了种说法，并没有真的解决这个问题。笔者认为，像 SimSiam、GAN 等模型的成功，很重要的原因是使用了基于梯度的优化器（而非其他更强或者更弱的优化器），所以不结合优化动力学的答案都是不完整的。在这里，笔者尝试结合动力学来分析 SimSiam 不会退化的原因。

SimSiam

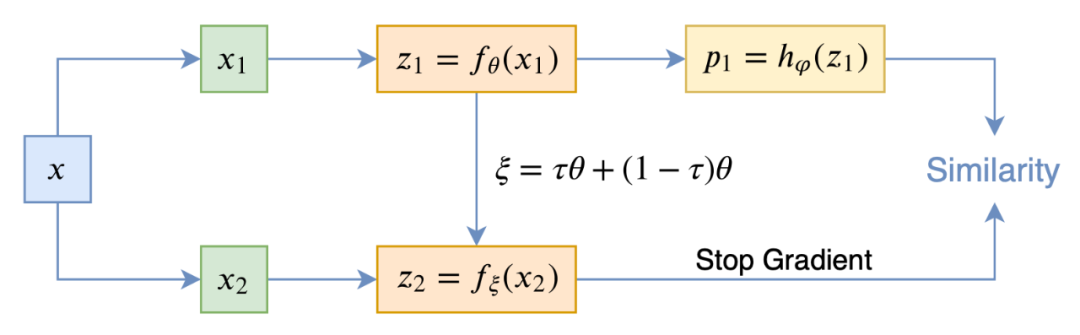
在看 SimSiam 之前，我们可以先看看 BYOL，来自论文 Bootstrap your own latent: A new approach to self-supervised Learning [4]  ，其学习过程很简单，就是维护两个编码器 Student 和 Teacher，其中 Teacher 是 Student 的滑动平均，Student 则又反过来向 Teacher 学习，有种“左脚踩右脚”就可以飞起来的感觉。示意图如下：

▲ BYOL示意图

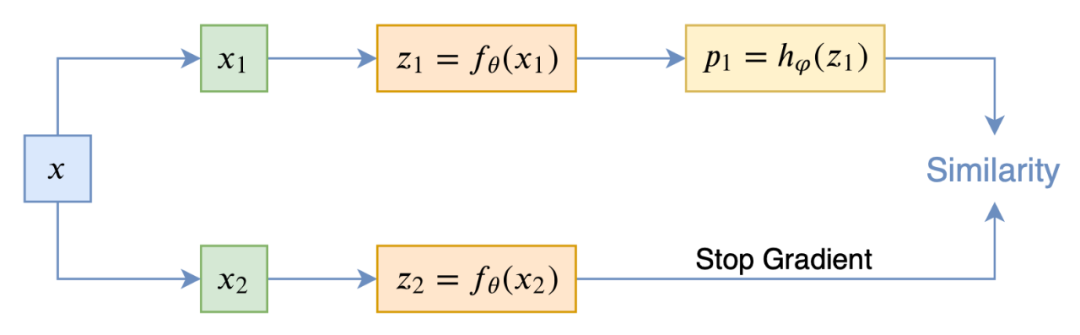
而 SimSiam 则来自论文 Exploring Simple Siamese Representation Learning [5]  ，它更加简单，直接把 BYOL 的滑动平均去掉了：

▲ SimSiam示意图

事实上，SimSiam 相当于将 BYOL 的滑动平均参数 设置为 0 了，这说明 BYOL 的滑动平均不是必须的。为了找出算法中的关键部分，SimSiam 还做了很多对比实验，证实了 stop_gradient 算子以及 predictor 模块 是 SimSiam 不退化的关键。为了解释这个现象，SimSiam 提出了该优化过程实际上相当于在交替优化：

其中 x 代表训练样本而 代表数据扩增。这部分内容网上已有不少解读，直接读原论文也不困难，因此就不详细展开了。

动力学分析

然而，笔者认为，将 SimSiam 算法的理解转换成 的交替优化的理解，只不过是换了种说法，并没有作出什么实质的回答。因为很明显，目前 也存在退化解，模型完全可以让所有的 都等于同一个向量，然后 输出同一个常数向量。不回答 的交替优化为什么不退化，那也等于没有回答问题。

下面笔者将列举出自认为是 SimSiam 不退化的关键因素，并且通过一个简单的例子表明回答不退化的原因需要跟动力学结合起来。当然，笔者这部分的论述其实也是不完整的，甚至是不严谨的，只是抛砖引玉地给出一个新的视角。

2.1 深度图像先验

首先，很早之前人们就发现一个随机初始化的 CNN 模型就可以直接用来提取视觉特征，效果也不会特别差，该结论可以追溯到 2009 年的论文 What is the best multi-stage architecture for object recognition? [6] ，这可以理解为 CNN 天然具有处理图像的能力。

后来这个特性被起了一个高大上的名字，称为“深度图像先验”，出自论文 Deep Image Prior [7] ，里边做了一些实验，表明从一个随机初始化的 CNN 模型出发，不需要任何监督学习，就可以完成图像补全、去噪等任务，进一步确认了 CNN 天然具有处理图像的能力这个特性。

按照笔者的理解，“深度图像先验”源于三点：

1. 图像的连续性，是指图像本身就可以直接视为一个连续型向量，而不需要像 NLP 那样要学习出 Embedding 层出来，这意味着我们用“原始图像 +K 邻近”这样简单粗暴的方法就可以做很多任务了；

2. CNN的架构先验，指的是 CNN 的局部感知设计确实很好地模拟了肉眼的视觉处理过程，而我们所给出的视觉分类结果也都是基于我们的肉眼所下的结论，因此两者是契合的；

3. 良好的初始化，这不难理解，再好的模型配上全零初始化了估计都不会 work，之前的文章从几何视角来理解模型参数的初始化策略 [8] 也简单讨论过初始化方法，从几何意义上来看，主流的初始化方法都是一种近似的“正交变换”，能尽量地保留输入特征的信息。

2.2 不退化的动力学

还是那句话，深度图像先验意味着一个随机化的 CNN 模型就是一个不是特别差的编码器了，于是我们接下来要做的事情无非可以归结为两点：往更好地方向学、不要向常数退化。

往更好地方向学，就是通过人为地设计一些先验信号，让模型更好地融入这些先验知识。SimSiam、BYOL 等让同一张图片做两种不同的数据扩增，然后两者对应的特征向量尽量地相似，这便是一种好的信号引导，告诉模型简单的变换不应当影响我们对视觉理解，事实上，这也是所有对比学习方法所用的设计之一。

不同的则是在“不要向常数退化”这一点上，一般的对比学习方法是通过构造负样本来告诉模型哪些图片的特征不该相近，从而让模型不退化；但是 SimSiam、BYOL 不一样，它们没有负样本，实际上它们是通过将模型的优化过程分解为两个同步的、但是快慢不一样的模块来防止退化的。还是以 SimSiam 为例，它的优化目标可以写为：

然后用梯度下降来优化，对应的动力学方程组是：

上式已经注明了有无 stop_gradient 算子所带来的差别。简单来说，如果添加了 stop_gradient 算子，那么 就少了第二项，这时候 都共同包含因子 ，由于 更靠近输出层，并且初始化的 也是一个不差的编码器，因此开始学习的时候， 会被优化得更快，越靠近输入层的优化得越慢。

也就是说， 是快动力学部分， 则是慢动力学部分，那么相对而言， 会更快速地收敛到 0，这意味着 会很快地变得很小，由于 也包含 这一项，所以 跟着变得小，在它退化之前，推动它退化的力都已经微乎其微了，也就不会退化了。

相反，如果有第二项 （不管是补充上它还是只保留它），那么就相当于添加了一个“快速通道”，使得它变为快速项，就算 ，但由于第二项在，还会继续推动着它退化。

举个简单的具体例子，我们考虑：

简单起见这里的 都是标量，对应动力学方程是：

假设 （随便选的），那么两者的演变是：

▲ 停掉第二个θ的梯度

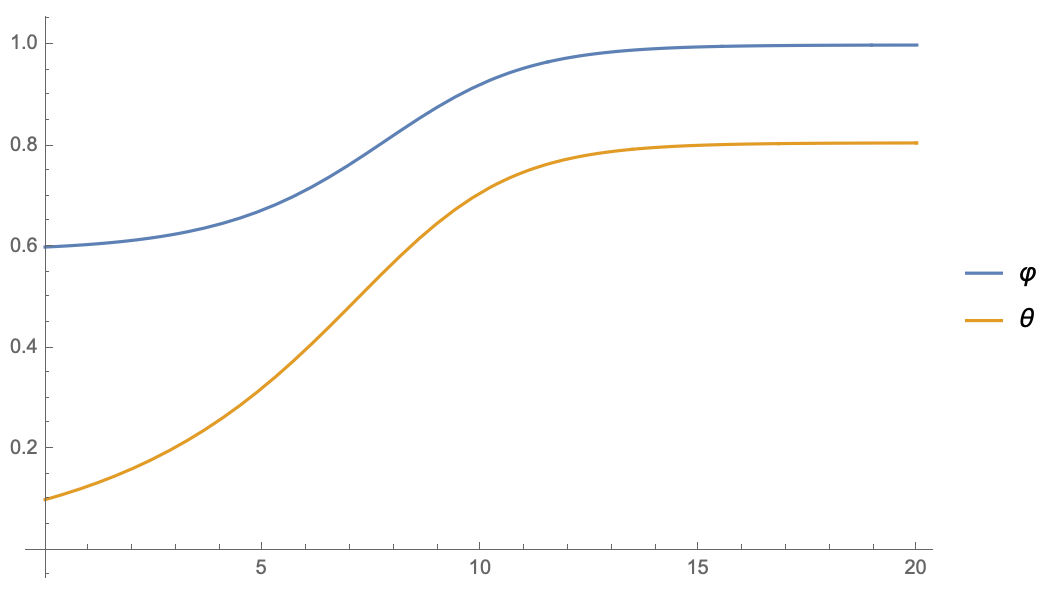
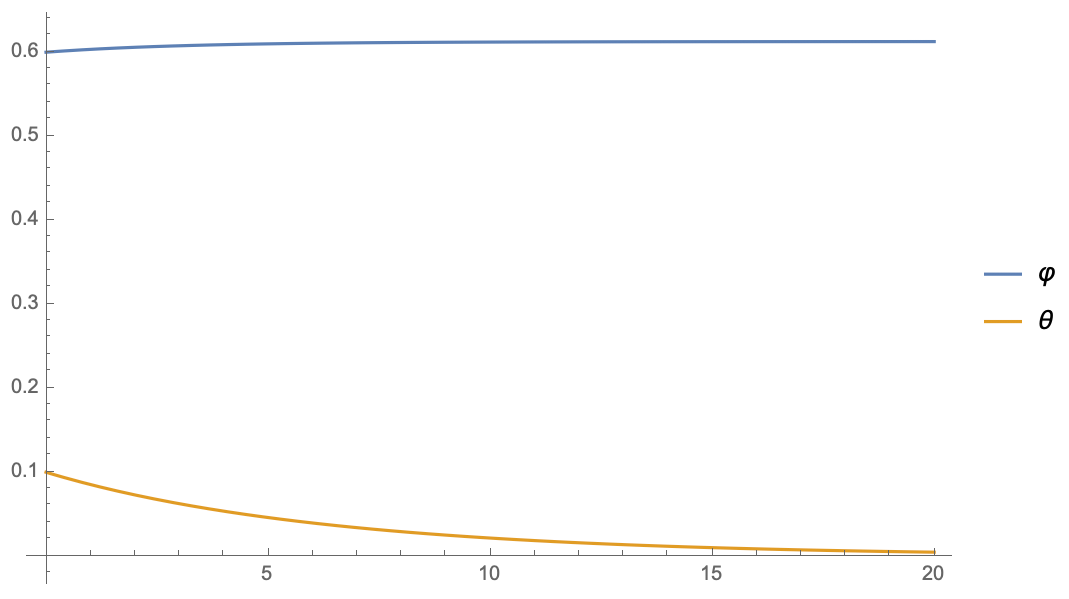
▲ 不停掉第二个θ的梯度

可以看到，停掉第二个 的梯度后， 和 的方程是相当一致的， 迅速趋于 1，同时 稳定到了一个非 0 值（意味着没退化）。相当，如果补充上 的第二项，或者干脆只保留第二项，结果都是 迅速趋于 0，而 则无法趋于 1 了，这意味着主导权被 占据了。

这个例子本身没多大说服力，但是它简单地揭示了动力学的变化情况：

predictor（ ）的引入使得模型的动力学分为了两大部分，stop_gradient 算子的引入则使得 encoder 部分（ ）的动力学变慢，并且增强了 encoder 与 predictor 的同步性，这样一来，predictor 以“迅雷不及掩耳之势”拟合了目标，使得 encoder 还没来得及退化，优化过程就停止了。

看近似展开

当然，诠释千万种，皆是“马后炮”，真正牛的还是发现者，我们充其量也就是蹭掉热度而已。这里再多蹭一下，分享笔者从另外一个视角看的 SimSiam。文章开头说了，SimSiam 论文提出了通过目标（1）的交替优化来解释 SimSiam，这个视角就是从目标（1）出发，进一步深究一下它不退化的原因。

如果固定 ，那么对于目标（1）来说，很容易解出 的最优值为：

代入（1），就得到优化目标为：

我们假定 是“小”的向量，那么在 x 处做一阶展开得到 ：

其中 是同一张图片在所有数据扩增手段下的平均结果，注意它通常不等于 x。类似地，如果是不加 stop_gradient 也不加 predictor 的 SimSiam，那么损失函数近似为：

在式（8）中，每个 减去了 ，可以证明这个选择能使得损失函数最小；而在式（9）中，每个 减去的是另一个扩增结果 ，会导致损失函数本身和估计的方差都大大增大。

那是不是意味着，不加 stop_gradient、不加 predictor 会失败的原因，是因为它的损失函数以及方差过大呢？注意到在一阶近似下有 ，那如果优化目标换成：

是不是就不会退化了？笔者也没有验证过，不得而知，正在研究相关内容的读者不妨验证一下。这里还引申出一个相关的问题，经过这样训练好的编码器，究竟用 还是 作为特征好呢？

当然，这部分的讨论都是建立在“ 是小的向量”这个假设的基础上的，如果它不成立，那么这一节内容就是白说了。

文末小结

本文试图从动力学角度给出笔者对 BYOL、SimSiam 算法不退化的理解，很遗憾，写到一半的时候发现之前头脑中构思的一些分析无法自圆其说了，于是删减了一些内容，并补充了一个新的角度，尽量让文章不“烂尾”，至于求精，那是说不上了。权当笔记分享在此，如有不当之处，还望读者海涵斧正。

参考文献

[1] https://arxiv.org/abs/2002.05709

[2] https://arxiv.org/abs/2006.07733

[3] https://arxiv.org/abs/2011.10566

[4] https://arxiv.org/abs/2006.07733

[5] https://arxiv.org/abs/2011.10566

[6] https://ieeexplore.ieee.org/document/5459469

[7] https://arxiv.org/abs/1711.10925

[8] https://kexue.fm/archives/7180

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。