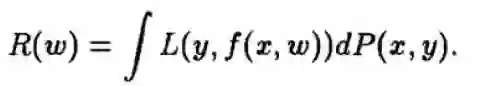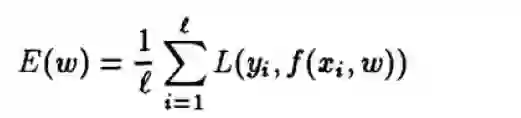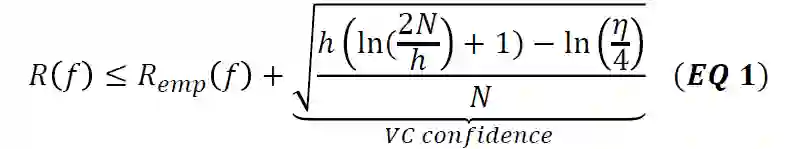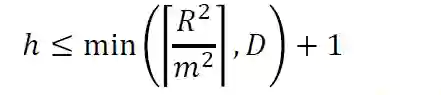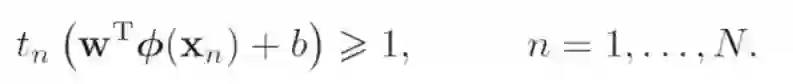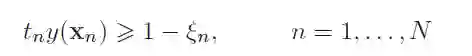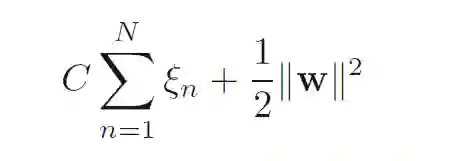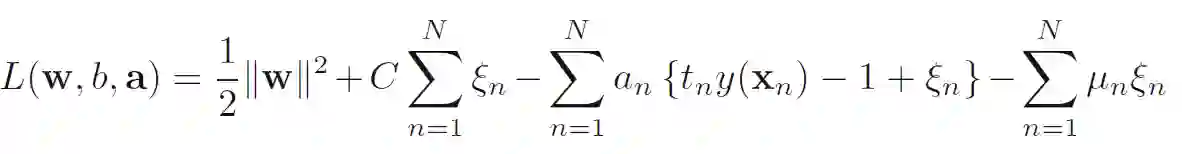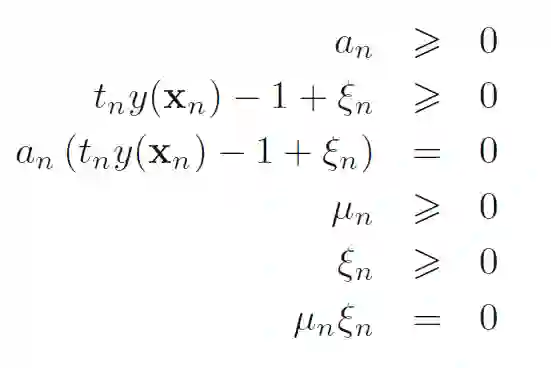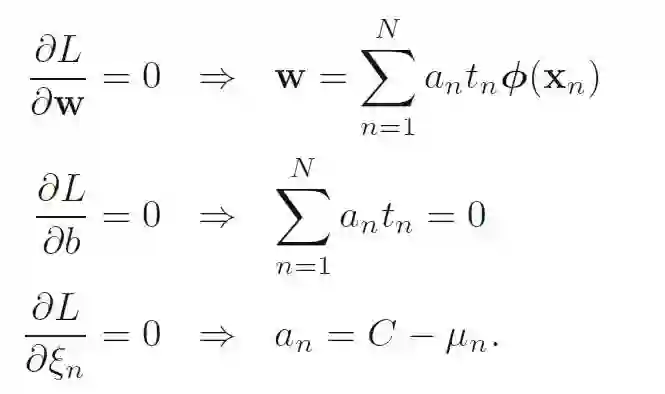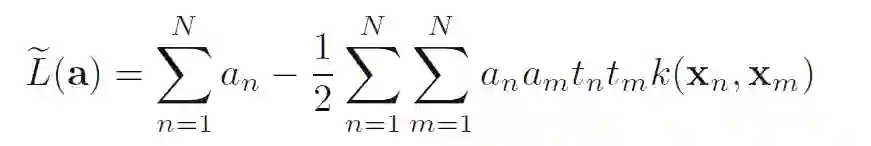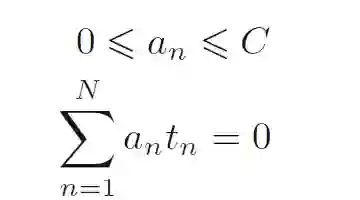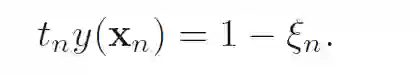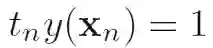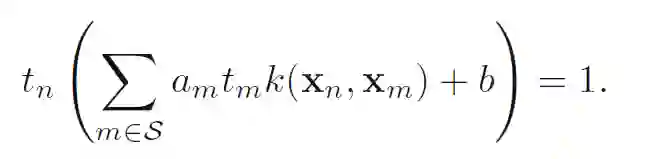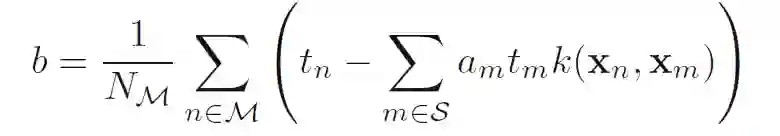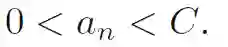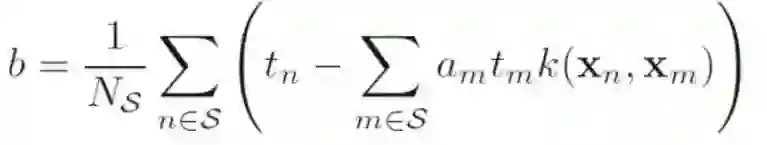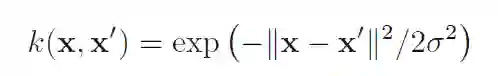[编程经验] TensorFlow实现非线性支持向量机

[点击蓝字，一键关注~]

上一次说的是线性支持向量机的原理和tf实现问题，把SVM的原理简单用公式推导了一下，SVM这块还有几个问题没有解释，比如经验风险，结构风险，VC维，松弛变量等。今天主要是解释几个概念然后实现非线性的支持向量机。

1.  风险最小化

  

期望风险

对于一个机器学习模型来说，我们的目的就是希望在预测新的数据的时候，准确率最高，风险最小，风险函数可以定义为：

其中L是损失函数，P（x，y）是训练数据和label标签的联合概率密度函数。这个风险函数的存在的问题是，我们无法知道x和y的联合概率密度，为什么？ 

想一下，如果能知道所有x和y的联合概率密度，我们还需要去做预测吗？显然不需要了。

对于机器学习任务来说，训练集其实就相当于是样本，测试集也是样本，总体是我们无法穷尽的一个东东，x和y的联合概率密度就是对总体的一个描述，所以上面那个风险函数是无法计算的，期望风险由此得来。想一想概率统计中的平均值和期望的区别，这里你就能想明白了。

既然期望风险无法得到，那么机器学习算法就转化为求经验风险最小，经验就对应的是训练集，训练集是我们可以获得的东西，所以可以称为经验。

经验风险：

上式就是经验风险，L是损失函数，xi和yi是训练集，w是参数，对比一下这个式子和上面那个式子，就发现，区别在于一个是求积分，一个是求和，显然简单多了。其实最小二乘估计就是采用的经验风险最小为优化目标的，甚至说大多数的机器学习算法都是求经验风险最小的那一个模型。

2. VC维，Vapnik-Chervonenkis dimension

首先VC维描述了一族函数的复杂程度，而且并不是模型越复杂那么它的泛化能力就越好。如果一个模型在训练集上表现的很好，那么它的泛化能力一般较差，也就是说，如果一个简单的模型在训练集表现好，那么它的泛化能力往往比较好。

考虑一个二分类问题，假设现在有D维实数空间中的N个点，每个点有两种可能情况，+1和-1。那么N个点就有2^N中可能，举个栗子，N=3的时候，就有{(000), (001), (010), (011), (100), (101), (110), (111) }  。

一般对VC维的解释都是函数集可以打乱（shattered）的最大数据集的数目，怎么理解这句话呢? 我觉得是，假如一个函数集f（a）的VC维为h， 那么至少存在一个包含h个样本的数据集，可以被函数集f（a）分开。注意这里是至少存在一个，所以不是说只要是包含h个样本的数据，都可以被shatter！

还是不能理解？ 举个栗子

假如在二维平面内有3个点，那么我们可以找到一个线性分类器，不论是哪一种可能的情况，都可以将这三个点正确分类。所以这个分类器的VC维就是3.

3. 结构风险最小化

结构风险一般表示为经验风险和置信风险的和

其中h是VC维，N是训练样本个数。当N/h变大的时候，N变大，h变小，置信风险趋于0，这时候结构风险约等于经验风险。也就是说当给定足够的样本的时候，结构风险就是经验风险。

而支持向量机是基于结构风险最小的，即使的经验风险和VC置信风险的和最小。

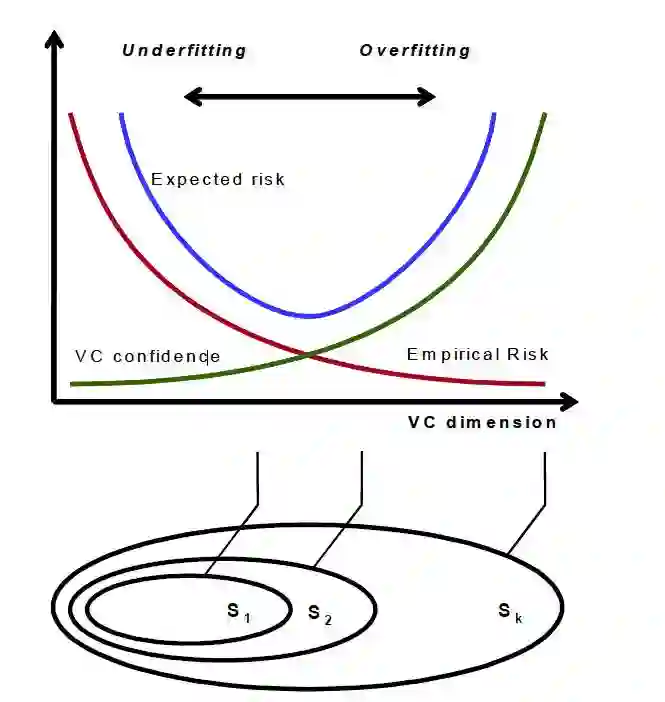
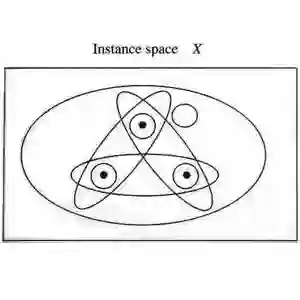
然后看下下面这个图，

下面的S1，S2，...，Sk表示的是不同VC维的函数族，当VC维增加的时候，经验风险在降低，置信风险却在增加，所以需要找到一个平衡点，这个平衡点就是最佳的模型。

到这里似乎问题已经解决了，但是VC维一般是很难计算的，尤其是对于像神经网络这样的非线性函数，Vapnik在1998年证明了下面这个公式：

其中m表示间隔（margin），D表示输入空间的维度，R是包含所有输入样本的组成的一个球体的最小的半径。上面这个式子说明，VC维最小等价于使得间隔最大，间隔最大也就是最小化经验风险的上界。

到这里其实是想说明，要使得结构风险最小，就要使得间隔最大。这就是为什么会提出支持向量机。

4. 松弛变量

上一次讲的时候，对于线性可分情况下，优化目标的约束条件是这个：

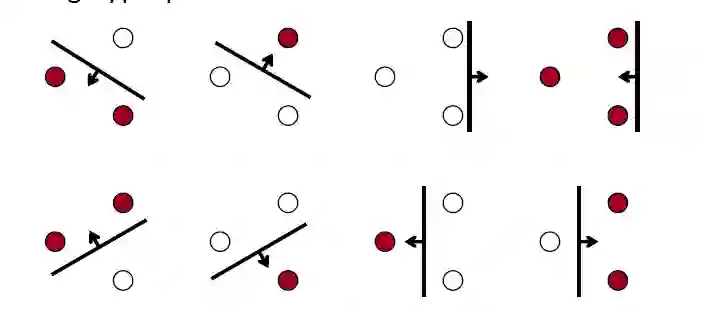
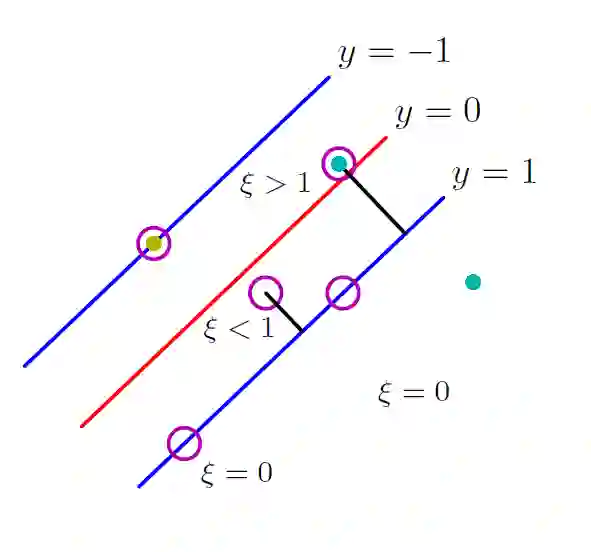
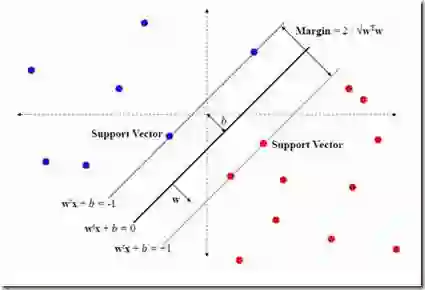
对于非线性可分情况下，就无法找到一个超平面来分类，为了实现最终分类，我们设计一种方法，使得用某一个超平面来分类的时候，误差最小。基于此，引入松弛变量，它表示了样本点与间隔的偏离，通俗点的理解是，对于非线性可分情况，有2种可能，一种是正类样本位于超平面的正确的一侧，虽然被正确分类，但是在间隔之内；还有一种可能是正类样本完全在负类样本中。下图是一个直观的解释，看图应该更容易理解。

上图中，凡是样本点在正类之外，松弛变量都是0，超平面右侧松弛变量小于1，左侧大于1。

引入松弛变量以后，约束条件就变为：

优化目标为：

其中C用来控制间隔和松弛变量之间的平衡关系；

还是用拉格朗日乘子法求解上述优化问题，只不过这里的乘子有2个，一个是a，一个是mu。

KKT条件：

分别令偏导数为0：

对偶形式：

对偶约束：

然后对KKT条件中第三个式子做个移项：

对于支持向量来说，松弛变量都是0，此时满足：

即：

求解上式就可以得到：

对比一下，线性可分情况：

其中Ns表示的是所有的支持向量。

我们发现，对于 非线性可分情况，其实就是为了去掉那些不是支持向量的点，使得最终还是满足线性可分。

最后大家可能对核函数怎么算的，不是很清楚，这里贴一个公式：

其中的函数fai，表示特征空间中的非线性映射关系；

常用的核函数，比如高斯核函数RBF：

对于怎么选择核函数，可以参考下面的参考文献。。。

下面就是如何用TF来实现非线性SVM了

# coding: utf-8
import numpy as np
import tensorflow as tf
from sklearn import datasets

x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
prediction = tf.placeholder(shape=[None, 2], dtype=tf.float32)


def get_data():
    iris = datasets.load_iris()
    x_vals = np.array([[x[0], x[3]] for x in iris.data])
    y_vals = np.array([1 if y == 0 else -1 for y in iris.target])
    return x_vals, y_vals


def Gaussian_kernel(gamma):
    g = tf.constant(gamma)
    # 2 * (x_data * x_data^T)
    sq_dists = tf.multiply(2.,
         tf.matmul(x_data, tf.transpose(x_data)))
    # exp(g * abs(sq_dists))
    out = tf.exp(tf.multiply(g, tf.abs(sq_dists)))
    return out


def non_linea_svm(my_kernel, batch_size, prediction, gamma=-25.0):
    b = tf.Variable(tf.random_normal(shape=[1, batch_size]))
    first_term = tf.reduce_sum(b)
    b_vec_cross = tf.matmul(tf.transpose(b), b)
    # 偏置的内积， b的转置乘以b
    y_target_cross = tf.matmul(y_target, tf.transpose(y_target))
    # label的内积，y乘以y的转置
    second_term = tf.reduce_sum(tf.multiply(my_kernel,
             tf.multiply(b_vec_cross, y_target_cross)))
    # 偏置的内积乘以label 的内积，结果再乘以核函数
    loss = tf.negative(tf.subtract(first_term, second_term))
    # 第一项和第二项做差，然后添加一个负号，
    # negative是取相反数的意思
    rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),
                                  [-1, 1])
    rB = tf.reshape(tf.reduce_sum(tf.square(prediction), 1), 
                              [-1, 1])
    stra = tf.subtract(rA, tf.multiply(2., 
            tf.matmul(x_data, tf.transpose(prediction))))
    pred_sq_dist = tf.add(stra, tf.transpose(rB))
    # (rA-2*x_data*预测值的转置）+rB的转置
    pred_kernel = tf.exp(tf.multiply(gamma, 
                      tf.abs(pred_sq_dist)))

    prediction_output = tf.matmul(tf.multiply(
                tf.transpose(y_target), b), pred_kernel)
    prediction = tf.sign(prediction_output -
                     tf.reduce_mean(prediction_output))
    accuracy = tf.reduce_mean(
        tf.cast(tf.equal(tf.squeeze(prediction), 
                tf.squeeze(y_target)), tf.float32))
    my_opt = tf.train.GradientDescentOptimizer(0.01)
    train_step = my_opt.minimize(loss)
    return loss, accuracy, train_step


def train_svm(sess, batch_size):
    kernel = Gaussian_kernel(-25.0)
    loss_vec = []
    batch_accuracy = []
    for i in range(300):
        x_vals, y_vals = get_data()
        loss, accuracy, train_step = non_linea_svm(
            kernel, batch_size=batch_size, 
                    prediction=prediction)
        init = tf.global_variables_initializer()
        sess.run(init)
        rand_index = np.random.choice(len(x_vals),
                       size=batch_size)
        rand_x = x_vals[rand_index]
        rand_y = np.transpose([y_vals[rand_index]])
        sess.run(train_step,
                 feed_dict={x_data: rand_x, 
                          y_target: rand_y})

        temp_loss = sess.run(loss,
                  feed_dict={x_data: rand_x,
                          y_target: rand_y})
        loss_vec.append(temp_loss)

        acc_temp = sess.run(accuracy,feed_dict={x_data: rand_x,
                          y_target: rand_y,
                          prediction: rand_x})
        batch_accuracy.append(acc_temp)

        if (i + 1) % 100== 1:
            print('Loss = ' + str(temp_loss))


def main(_):
    with tf.Session() as sess:
        train_svm(sess, batch_size=30)


if __name__ == "__main__":
    tf.app.run()

最后说一下，哪里有看不懂的，欢迎与我交流~~

参考文献：

1. Pattern Recognition and Machine Learning

2. machine Learning A Probabilistic Perspective 

3. Introduction to Machine Learning 

4. https://www.zhihu.com/question/21883548