你还在为查询滑动窗口最大值发愁吗？点开看最高效率解法！

作者 | 王磊

来源 | Java中文社群（ID：javacn666）

头图 |  CSDN 下载自东方IC

本文已收录至 Github《小白学算法》系列：https://github.com/vipstone/algorithm

这是一道比较基础的算法题，涉及到的数据结构也是我们之前讲过的，我这里先买一个关子。这道面试题最近半年在亚马逊的面试中出现过 28 次，在字节跳动中出现过 7 次，数据来源于 LeetCode。

我们先来看题目的描述。

题目描述

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

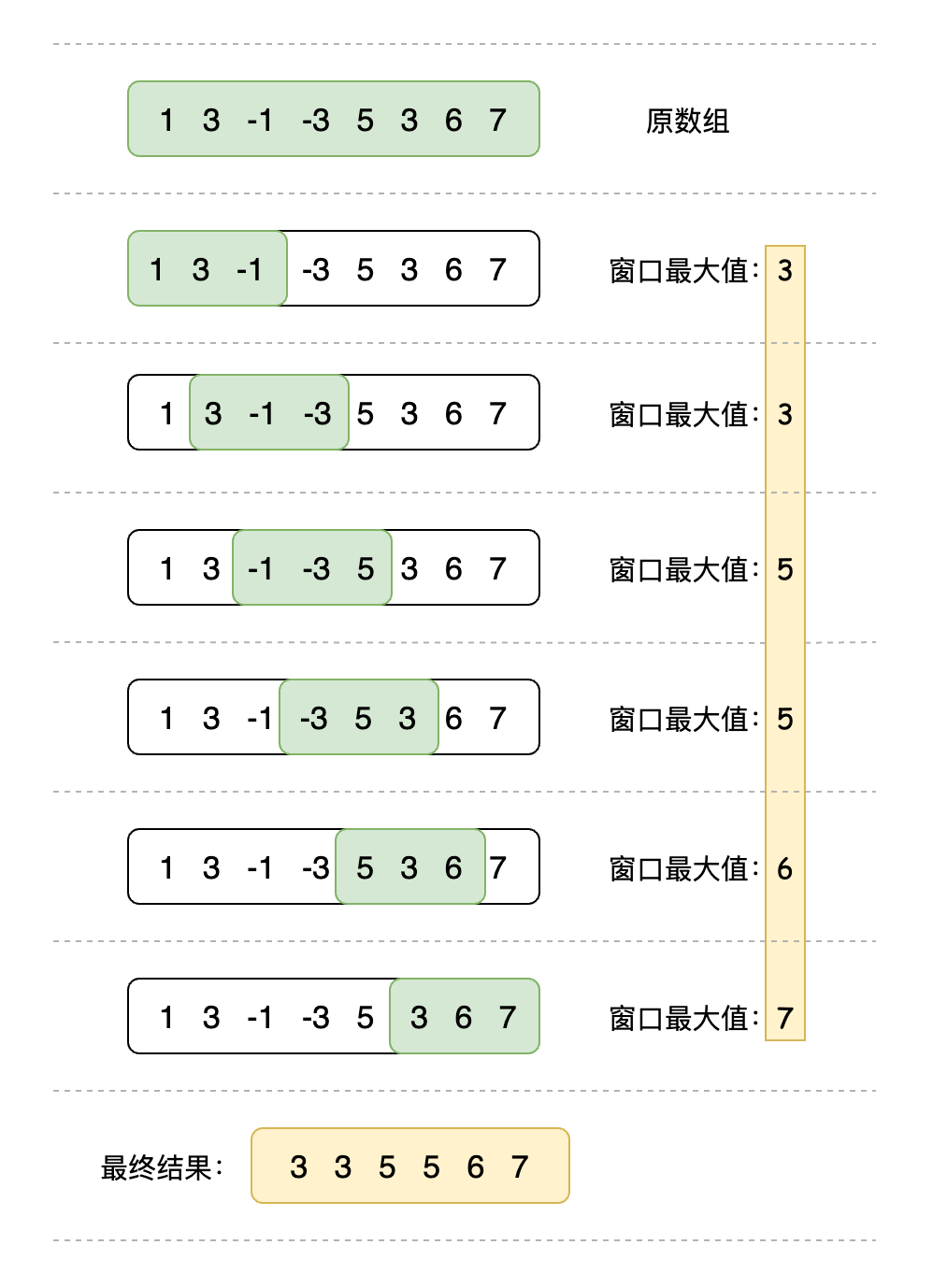
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7]

提示：你可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的大小。

LeetCode：https://leetcode-cn.com/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/

题目解析

上面的题目看不懂？没关系，接下来来看这幅图可以清楚的描述这道题：

从上述图片可以看出，题目的意思为：给定一个数组，每次查询 3 个元素中的最大值，数量 3 为滑动窗口的大小，之后依次向后移动查询相邻 3 个元素的最大值。图片中的原始数组为 [1,3,-1,-3,5,3,6,7]，最终滑动窗口的最大值为 [3,3,5,5,6,7]。

看到这个题之后，我们的第一直觉就是暴力解法，用两层循环依次查询滑动窗口的最大值，实现代码如下。

实现方法 1：暴力解法

暴力解法的实现思路和实现代码很直观，如下所示：

class Solution {      public int[] maxSlidingWindow(int[] nums, int k) {            // 非空判断            if (nums == null || k <= 0) return new int[0];            // 最终结果数组            int[] res = new int[nums.length - k + 1];            for (int i = 0; i < res.length; i++) {                // 初始化最大值                int max = nums[i];                 // 循环 k-1 次找最大值                for (int j = i + 1; j < (i + k); j++) {                  max = (nums[j] > max) ? nums[j] : max;              }              res[i] = max;        }          return res;    }}

把以上代码提交至 LeetCode，执行结果如下：

从上述结果可以看出，虽然代码通过了测试，但执行效率却很低，这种代码是不能应用于生产环境中的，因此我们需要继续找寻新的解决方案。

实现方法 2：改良版

接下来我们稍微优化一下上面的方法，其实我们并不需要每次都经过两层循环，我们只需要一层循环拿到滑动窗口的最大值（之前循环元素的最大值），然后在移除元素时，判断当前要移除的元素是否为滑动窗口的最大值，如果是，则进行第二层循环来找到新的滑动窗口的最大值，否则只需要将最大值和新增的元素比较大小即可，实现代码如下：

class Solution {    public int[] maxSlidingWindow(int[] nums, int k) {        // 非空判断        if (nums == null || k <= 0) return new int[0];        // 最终结果数组        int[] res = new int[nums.length - k + 1];        // 存储的数据为元素的下标        ArrayDeque<Integer> deque = new ArrayDeque();        for (int i = 0; i < nums.length; i++) {            // 1.移除左边超过滑动窗口的下标            if (i >= k && (i - k) >= deque.peek()) deque.removeFirst();
            // 2.从最后面开始移除小于 nums[i] 的元素            while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i])                deque.removeLast();
            // 3.下标加入队列            deque.offer(i);
            // 4.将最大值加入数组            int rindex = i - k + 1;            if (rindex >= 0) {                res[rindex] = nums[deque.peek()];            }        }        return res;    }}

把以上代码提交至 LeetCode，执行结果如下：

从上述结果可以看出，改造之后的性能基本已经符合我的要求了，那文章开头说过这道题还可以使用我们之前学过的数据结构？那它说的是什么数据结构呢？

其实我们可以使用 「队列」 来实现这道题目，它的实现思路也非常简单，甚至比暴力解法更加方便，接下来我们继续往下看。

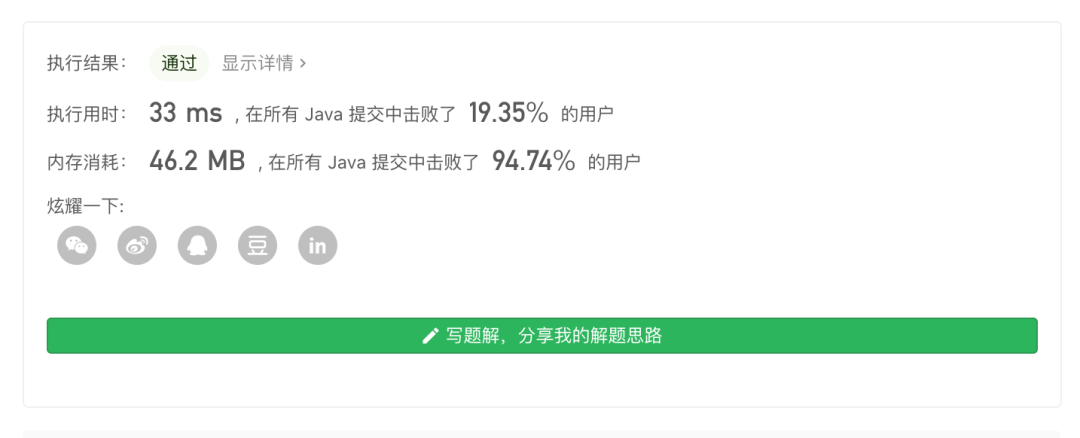
实现方法 3：优先队列

这个题的另一种经典的解法，就是使用最大堆的方式来解决，最大堆的结构如下所示：

最大堆的特性是堆顶是整个堆中最大的元素。

我们可以将滑动窗口的值放入最大堆中，这样利用此数据结构的特点（它会将最大值放到堆顶），因此我们就可以直接获取到滑动窗口的最大值了， 实现代码如下：

class Solution {    public int[] maxSlidingWindow(int[] nums, int k) {        // 非空判断        if (nums == null || k <= 0) return new int[]{};        // 最终结果数组        int[] res = new int[nums.length - k + 1];        // 优先队列        PriorityQueue<Integer> queue = new PriorityQueue(res.length, new Comparator<Integer>() {            @Override            public int compare(Integer i1, Integer i2) {                // 倒序排列（从大到小，默认是从小到大）                return i2 - i1;            }        });        // 第一轮元素添加        for (int i = 0; i < k; i++) {            queue.offer(nums[i]);        }        res[0] = queue.peek();        int last = nums[0]; // 每轮要移除的元素        for (int i = k; i < nums.length; i++) {            // 移除滑动窗口之外的元素            queue.remove(last);            // 添加新元素            queue.offer(nums[i]);            // 存入最大值            res[i - k + 1] = queue.peek();            // 记录每轮要移除的元素（滑动窗口最左边的元素）            last = nums[i - k + 1];        }        return res;    }}

代码解读

从上述代码可以看出：最大堆在 Java 中对应的数据结构就是优先级队列 PriorityQueue，但优先级队列默认的排序规则是从小到大进行排序的，因此我们需要创建一个 Comparator 来改变一下排序的规则（从大到小进行排序），之后将滑动窗口的所有元素放入到优先级队列中，这样我们就可以直接使用 queue.peek() 拿到滑动窗口的最大值了，然后再循环将滑动窗口的边缘值移除掉，从而解决了本道题目。

把以上代码提交至 LeetCode，执行结果如下：

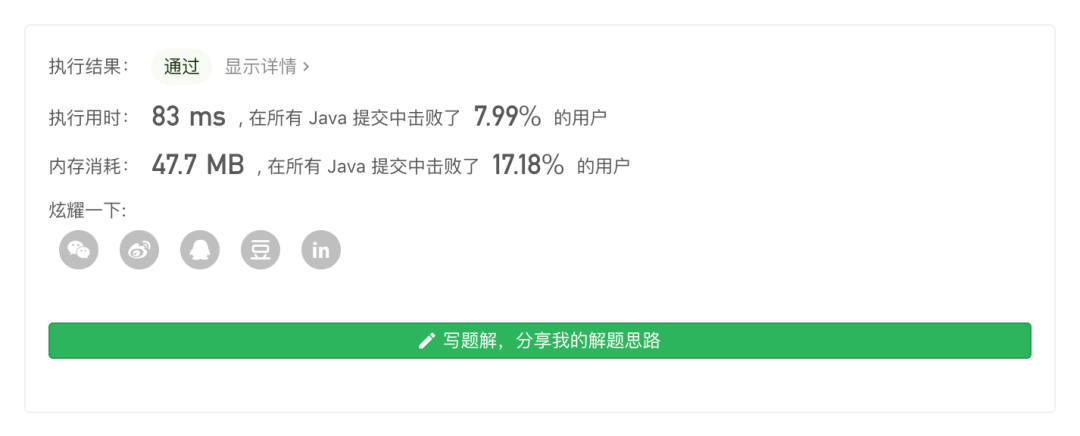
PS：从上面的执行结果可以看出，使用优先队列的执行效率很低，这是因为每次插入和删除都需要重新维护最大堆的元素顺序，因此整个执行的效率就会很低。

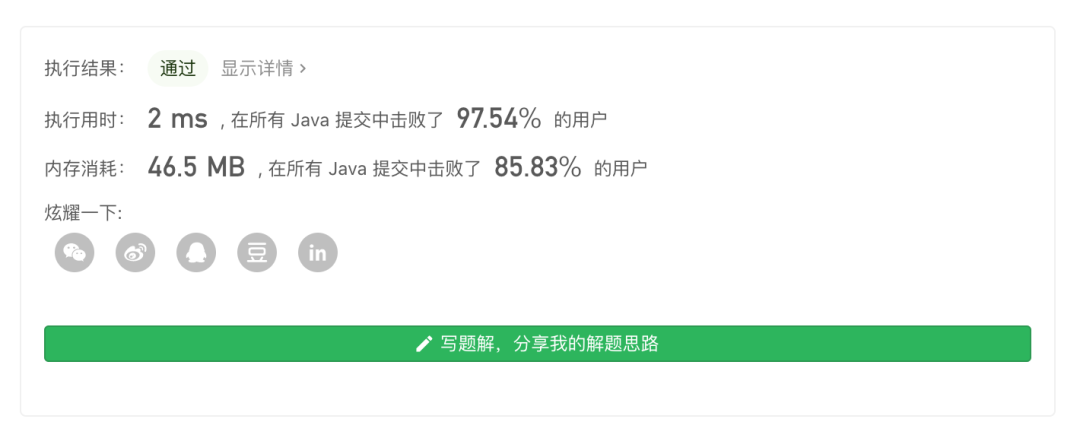
实现方法 4：双端队列

除了优先队列之外，我们还可以使用双端队列来查询滑动窗口的最大值，它的实现思路和最大堆的实现思路很像，但并不需要每次在添加和删除时进行元素位置的维护，因此它的执行效率会很高。

双端队列实现思路的核心是将滑动窗口的最大值始终放在队首位置（也就是队列的最左边），将小于最大值并在最大值左边（队首方向）的所有元素删除。这个也很好理解，因为这些相对较小的值既没有最大值大，又在最大值的前面，也就是它们的生命周期比最大值还短，因此我们可以直接将这些相对较小的元素进行删除 ，如下图所示：

像以上这种情况下，我们就可以将元素 1 和元素 2 删掉。

双端队列实现查询滑动窗口最大值的流程分为以下 4 步：

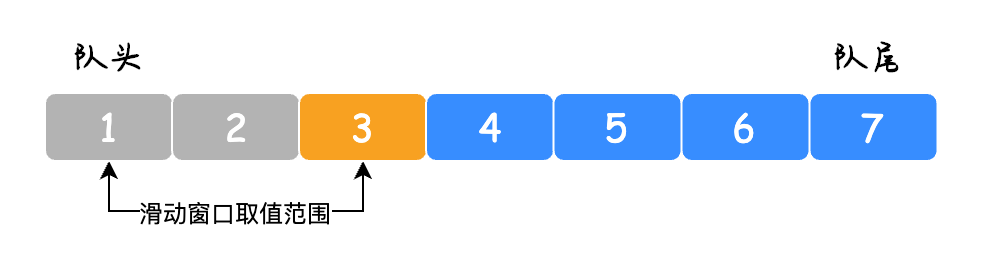
1. 移除最左边小于最大值的元素（保证滑动窗口的最大值在队首位置）；
2. 从队尾向前依次移除小于当前要加入到队列元素的值（淘汰小值且生命周期短的元素）；
3. 将新元素加入到队列末尾；
4. 将最大值加入到最终结果的数组中。

实现代码如下：

class Solution {    public int[] maxSlidingWindow(int[] nums, int k) {        // 非空判断        if (nums == null || k <= 0) return new int[]{};        // 最终结果数组        int[] res = new int[nums.length - k + 1];        // 优先队列        PriorityQueue<Integer> queue = new PriorityQueue(res.length, new Comparator<Integer>() {            @Override            public int compare(Integer i1, Integer i2) {                // 倒序排列（从大到小，默认是从小到大）                return i2 - i1;            }        });        // 第一轮元素添加        for (int i = 0; i < k; i++) {            queue.offer(nums[i]);        }        res[0] = queue.peek();        int last = nums[0]; // 每轮要移除的元素        for (int i = k; i < nums.length; i++) {            // 移除滑动窗口之外的元素            queue.remove(last);            // 添加新元素            queue.offer(nums[i]);            // 存入最大值            res[i - k + 1] = queue.peek();            // 记录每轮要移除的元素（滑动窗口最左边的元素）            last = nums[i - k + 1];        }        return res;    }}

把以上代码提交至 LeetCode，执行结果如下：

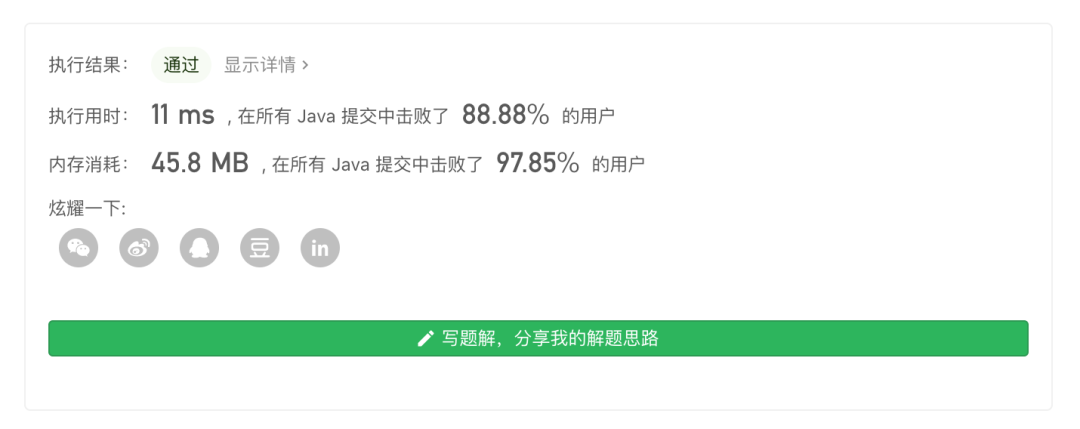
从上述结果可以看出，双端队列相比于优先级队列来说，因为无需重新计算并维护元素的位置，所以执行效率还是挺高的。

总结

本文我们通过 4 种方式实现了查找滑动窗口最大值的功能，其中暴力解法通过两层循环来实现此功能，代码最简单但执行效率不高，而通过最大堆也就是优先队列的方式来实现（本题）虽然比较省事，但执行效率不高。因此我们可以选择使用双端队列或改良版的代码来实现查询滑动窗口的最大值。

福 利
CSDN旗下公众号全新搜索技能上线啦！
只要在公众号内回复消息
就能自动回复想搜索的内容啦！

现在体验有惊喜，每日参与搜索打卡，
连续打卡满3天、7天、14天
均有CSDN精美礼品相送 百分百有礼！快戳
每日体验CSDN公众号搜索功能打卡

更多精彩推荐
☞倪光南、求伯君“出山”：爱解 Bug、无惧“35岁魔咒”、编码之路痛并快乐！
☞饿了么技术往事
☞我坦白！我是第五位飞上太空的程序员游客
☞赠书 | 图像分类问题建模方案探索实践
☞大神们都是如何在时间序列中进行特征提取的？看完就懂了！
☞Value DeFi遭黑客攻击始末，闪电贷这次又带走了700万美元
点分享
点点赞
点在看