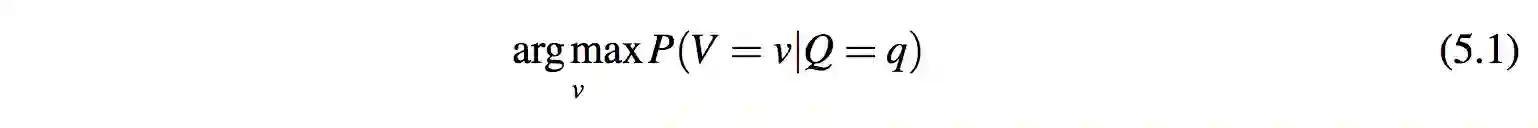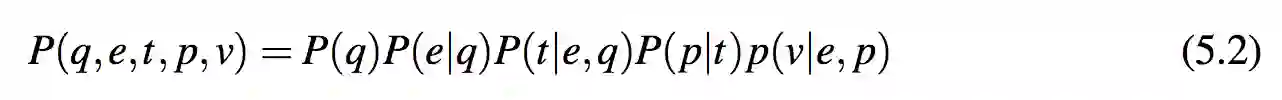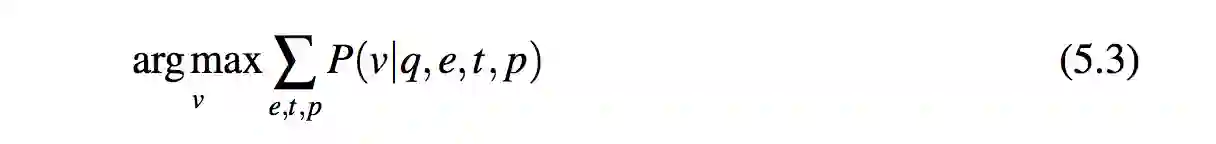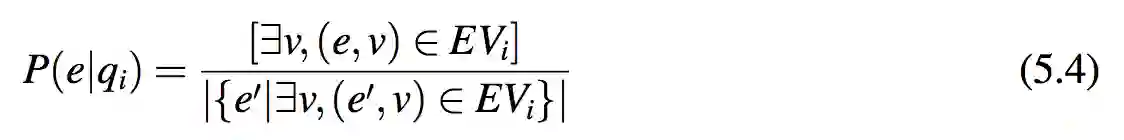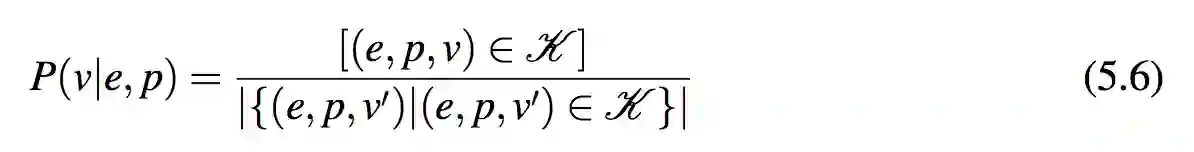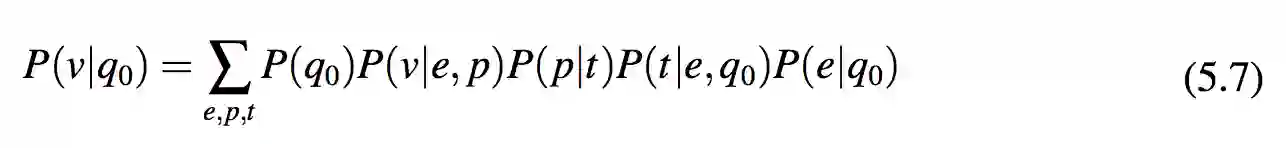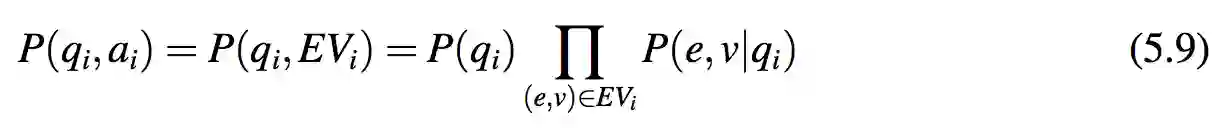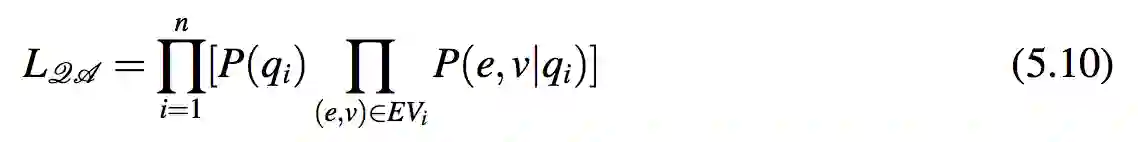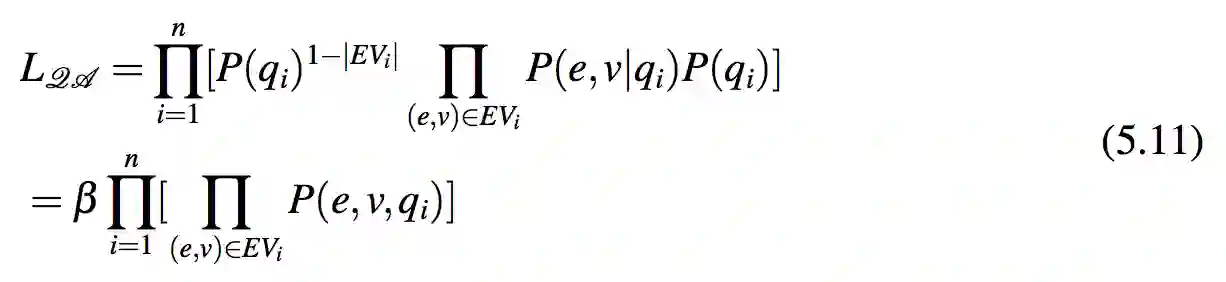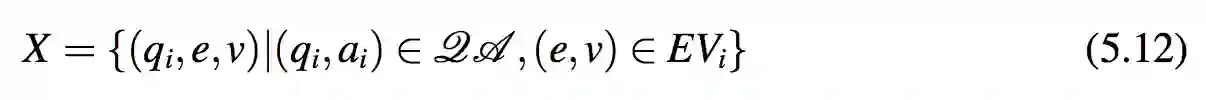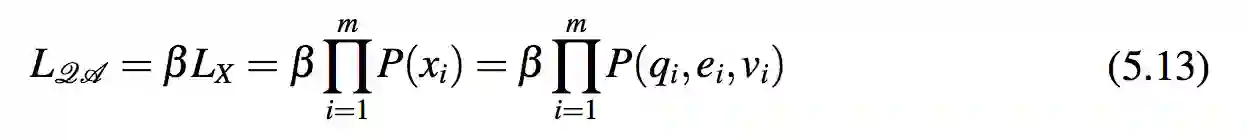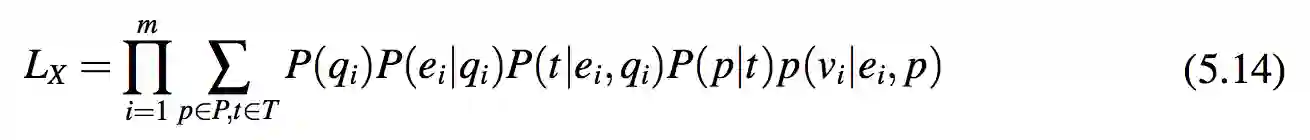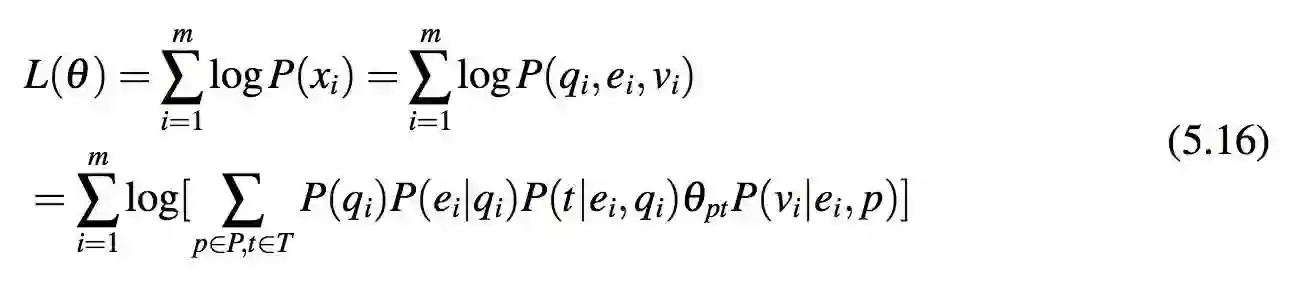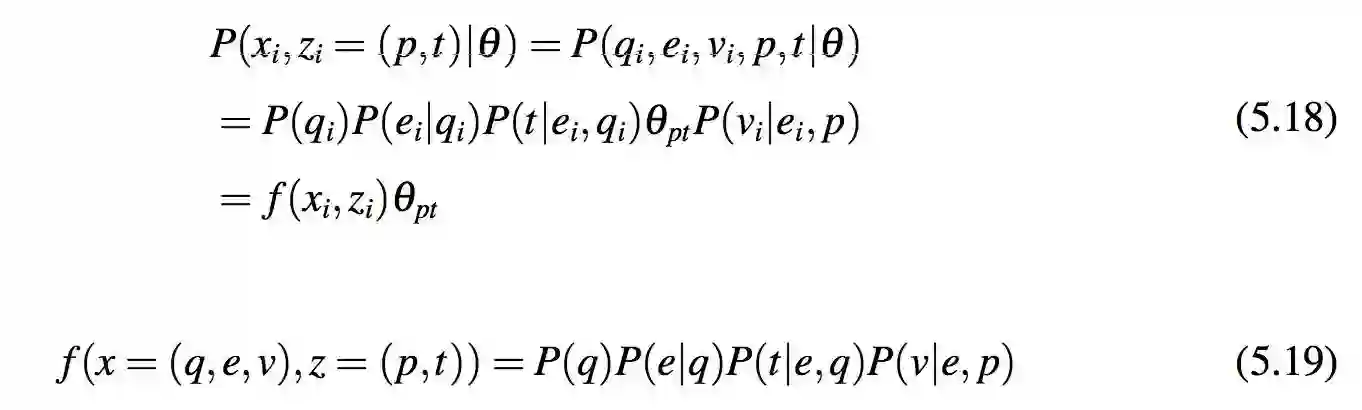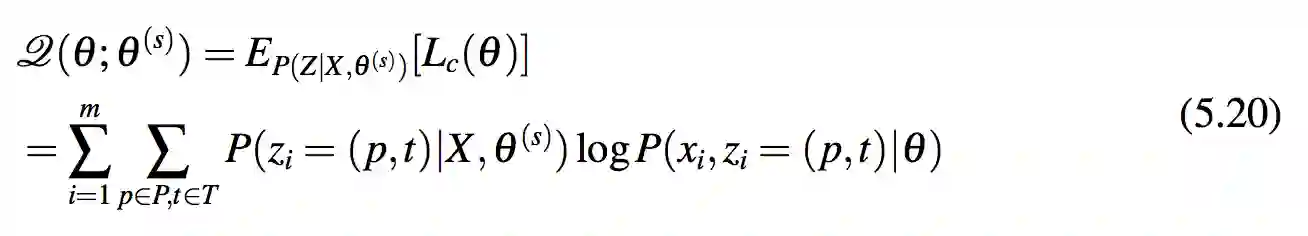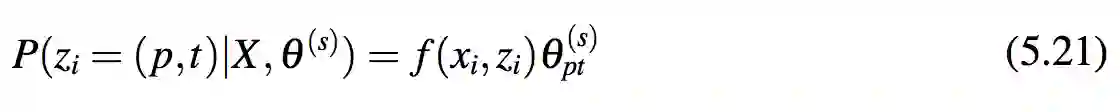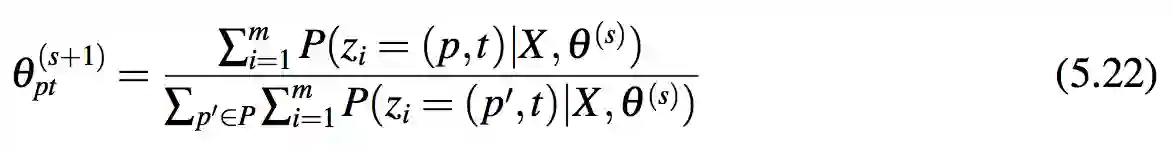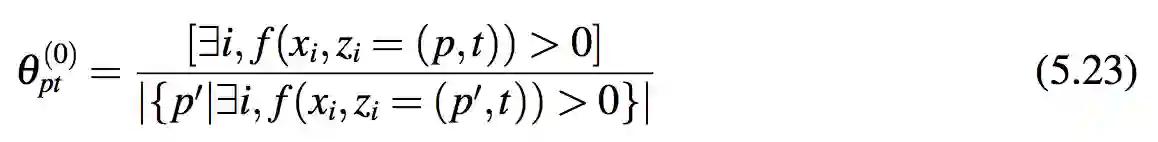论文动态 | 基于知识图谱的问答系统关键技术研究 #02

2017 年 8 月 6 日 开放知识图谱 崔万云

本文转载自 PaperWeekly 公众号，作者为崔万云，复旦大学知识工场实验室博士生，研究方向为问答系统和知识图谱。

第五章从问答语料库和知识图谱学习问答

问答系统（QA）已经成为人类访问十亿级知识图谱的流行方式。与网络搜索不同，在自然语言问题能够被精确地理解和映射到知识图谱上的结构化查询的前提下，基于知识图谱的问答系统将给出准确且简洁的结果。这其中的挑战是人类可以以许多不同的方式提出同一询问。现有的解决方案由于它们的模型表示而有着天然的缺陷：基于规则的实现只能理解一小部分的问题，而基于关键词或同义词的实现不能完整地理解问题。在十亿规模的知识图谱和百万规模的问答语料库的基础上，本章设计了一种新的问题表现形式：问题模板。例如，对于一个关于某个城市人口数目的问题，可以学习到诸如 what is the total number of people in $city? 或 how many people are there in $city? 这样的问题模板。本章共为 2782 种关系学习了约两千七百万种模板。基于这些模板，本章设计的问答系统 KBQA 能够有效地支持二元事实型问题，以及由一系列二元事实型问题组合而成的复杂问题。此外，通过将 RDF 知识图谱进行属性扩展，知识图谱的覆盖范围提高了 57 倍。在 QALD 标准测试集上，KBQA 系统在有效性和效率上击败了其他所有竞争对手。

第 1 节绪论

问答系统（QA）已吸引了大量的研究。一个 QA 系统是被设计用于回答某种特定类型的问题[12]。这其中最重要的一种问题类型是事实型问题（factoid ques- tion，FQ），这些问题询问有关某个实体的客观事实情况。一种特定的事实型问题是二元事实型问题（binary factoid question，BFQ）[1]，这些问题询问某个实体的一种属性。例如，How many people live in Honolulu? 是一个二元事实型问题。如果系统能回答 BFQ，那么它就有能力去回答其他种类的问题，比如 1)排序问题：Which city has the third largest population? 2)比较问题：Which city has more population, Honolulu or New Jersey? 3)列举问题：List the cities ordered by their populations等。除了 BFQ 及其变种之外，系统还能回答像 When was Barack Obama’s wife born? 这样的复杂的事实型问题。这一问题的回答可以通过合并两个 BFQ 的回答来实现：Who is the wife of Barack Obama (Michelle Obama) 和 When was Michelle Obama born? (1964)。系统将复杂事实型问题定义为那些可以分解成一系列 BFQ 的问题。本章将重点讨论 BFQ 和如前所述的复杂事实型问题。

基于知识图谱的 QA 已经有了较长的历史。最近，大规模知识图谱，如 Google Knowledge Graph, Freebase[10], YAGO2[45]等，不断涌现，极大地增加了问答系统的重要性和商业价值。大部分这样的知识图谱采用了 RDF 作为数据格式，并且它们包含数以百万或是十亿的 SPO 三元组(S，P，O分别表示主体，属性，宾语)。

1.1. 方法概览

图 5.1：基于模板的方法

为了回答一个问题，系统需要首先表示这个问题。所谓表示一个问题，指的是将问题从自然语言转换为一种能够捕获问题语义和意图的计算机内部表示。然后，对于每种内部表示，学习将其映射到知识图谱上的 RDF 查询。因此，本章工作的核心之一就是这一内部表示设计，记为“问题模板”。

通过模板表现问题 基于同义词的方法在问题 ○a 上的失败，启发系统通过模板来理解问题。例如，how many people are there in $city 是问题 ○a 的模板。无论 $city 指的是檀香山市还是其他城市，这一模板永远询问人口数的问题。

这样，问题表示的任务转化为了将问题映射到现有模板的任务。为了完成这一点，系统将问题中的实体替换为它的概念。如图 5.1，Honolulu 会被 $city 所替代。这一过程并不是直接的。它通过一种称为概念化[87, 50]的机制完成目的。这一机制会自动对输入进行歧义消除（因此苹果的总部是什么中的苹果会被概念化为 $company 而非 $fruit）。概念化机制本身基于一个考虑数百万种概念的语义网络（Probase [103]），其拥有足够的粒度来模板化所有类型的问题。

模板的思想对于复杂问题同样起效。通过使用模板，可以将复杂问题简单地分解为一系列仅对应一个属性的简单问题。以表 1.1 中的问题 ○f 为例，系统将 ○f 分解为 Barack Obama’s wife 和 when was Michelle Obama born。这两个子问题分别对应

“marriage→person→name”和“date of birth”。由于第一个问题嵌套于第二个问题，可知“date of birth”修饰了“marriage→person→name”，而“marriage→ person→name”修饰了 Michelle Obama。

将模板映射到属性 系统从雅虎问答（Yahoo! Answers）中学习模板以及如何将模板映射到知识图谱中的属性。这一问题与语义解析[13, 14]类似。从模板到属性的映射是多对一的，换言之，每个属性都对应于多个问题模板。系统一共学习了 2782 个属性的 27, 126, 355 种不同的模板。这一巨大的数目保证了基于模板的问答系统的高覆盖率。

学习模板的属性的过程如下所述。首先，对于每个雅虎问答中的问答对，系统提取问题中的实体及其对应值。之后，寻找连接实体和值的“直接”属性。其基本想法是，如果某个模板的绝大多数实例对应于共同的属性，就可以将这一模板映射到这一属性上。例如，假设从模板 how many people are there in$city 中得出的问题总是可以映射到属性“population”上，无论 $city 特指哪个城市，系统都可以认为这一模板必然会映射到属性“population”上。从模板到知识图谱中复杂结构的学习也采用类似的过程。唯一的区别在于系统寻找对应于一条由多条边组成的，从某个实体导向某个特定值的路径的“扩展属性”。（例如marriage→person→name）。

本章组织 本章余下部分的组织形式如下。在第 2 节中，将会给出 KBQA 的概览。本章的主要贡献是从 QA 语料库中学习模板以及通过模板回答自然语言问题。全部技术部分都与这一核心贡献紧密相关。第三节展示了系统如何在线上问答中使用模板。第四节详述了如何从模板中推断属性。这也是基于模板的问答系统的关键步骤。第五节扩展了解决方案，用于回答可以分解为一系列 BFQ 的复杂问题。第六节扩展了模板的能力来推断复杂的属性结构。实验结果呈现在第 7 节，第 8 节讨论了更多的相关工作。第 9 节做出了小结。

第 2 节系统概览

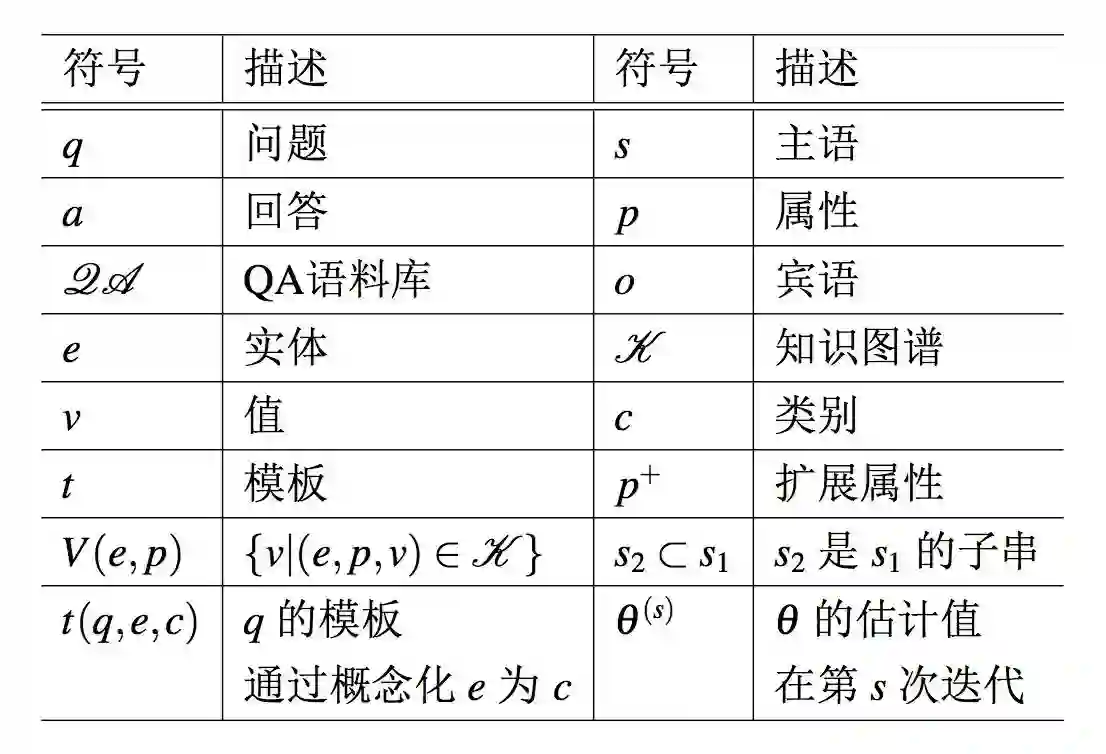
本节将要介绍 KBQA 的一些背景知识及其概览。表 5.1 中列举了本章使用的符号。

表 5.1：符号表

二元事实型 QA 本章主要关注二元事实型问题（BFQ），亦即询问某个实体的某种属性的问题。例如，表 1.1 中除 ○f 外的所有问题均为 BFQ。

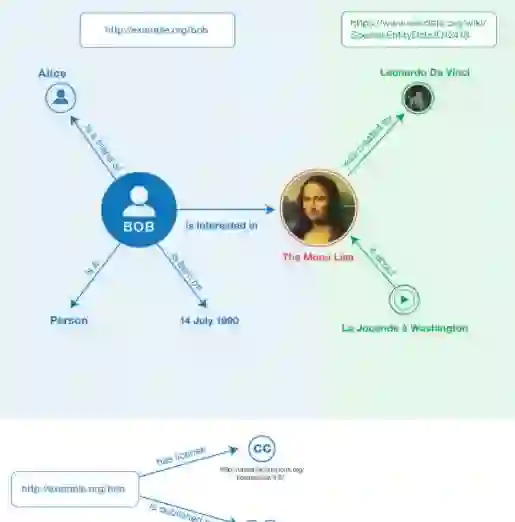
RDF 知识图谱 给定一个问题，系统在一个 RDF 知识图谱中寻找其回答。一个 RDF 知识图谱 K 是一个（s,p,o）格式三元组的集合，这里 s, p, o 分别表示主语，属性和宾语。图 1.1 通过一个边带标注的有向图展示了一个示例的 RDF 知识图谱。每个（s, p, o）都由一条从 s 指向 o，标注有属性 p 的边表示。例如，从 a 指向 1961 的标注有 dob 的边表示 RDF 三元组（a,dob,1961），意味着 Barack Obama 出生于 1961 年。

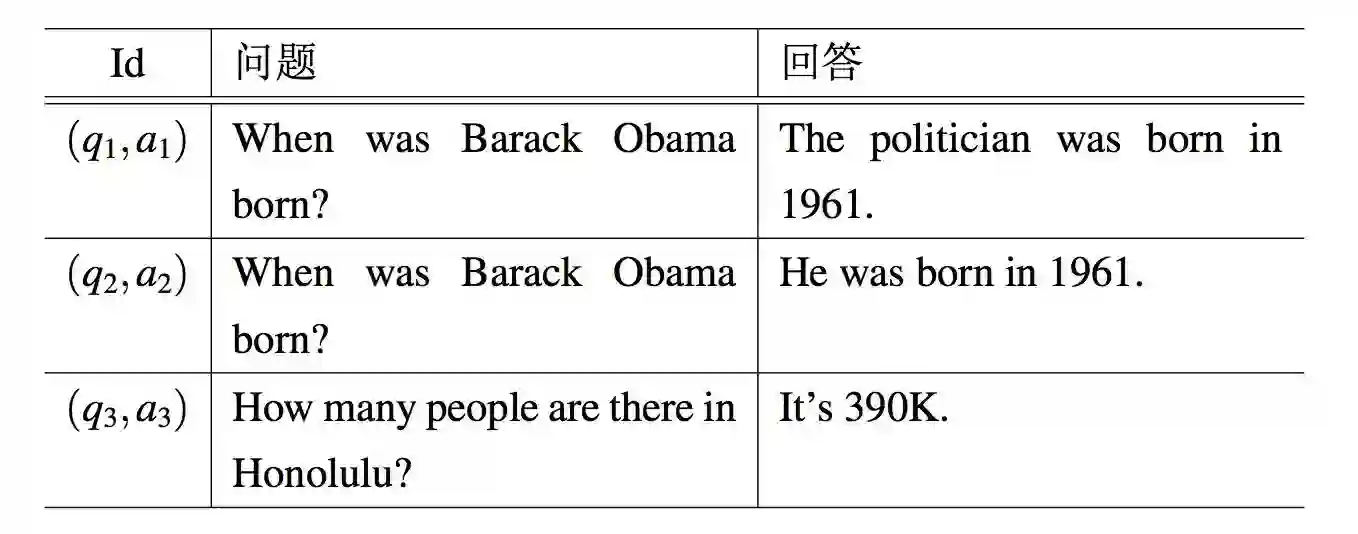
QA语料库 系统从雅虎问答学习问题模板，其包含有约四千一百万对问答对。这一 QA 语料库被记为 QA = {(q1,a1),(q2,a2),...,(qn,an)}，其中 qi 是某个问题而 ai 是其回复。每个回复 ai 含有一个或多个句子，并且确切的事实回答也被包含在回复中。表 5.2 展示了 QA 语料库中的一些例子。

表 5.2：QA 语料库中的 QA 对示例

模板通过用实体 e 的一个概念 c 替换 e，可以从问题 q 中得到模板 t。这一模板记为 t=t(q,e,c)。一个问题可能含有多个实体，并且一个实体可能属于多个概念。系统通过上下文相关的概念化过程[103]获得 e 的概念分布。例如，问题 when was Barack Obama born? 中含有图 1.1 中的实体 a。由于 a 属于两个概念：$person 和 $politician，系统可以从这一问题中获得两个模板：When was $person born? 和 When was $politician born?。

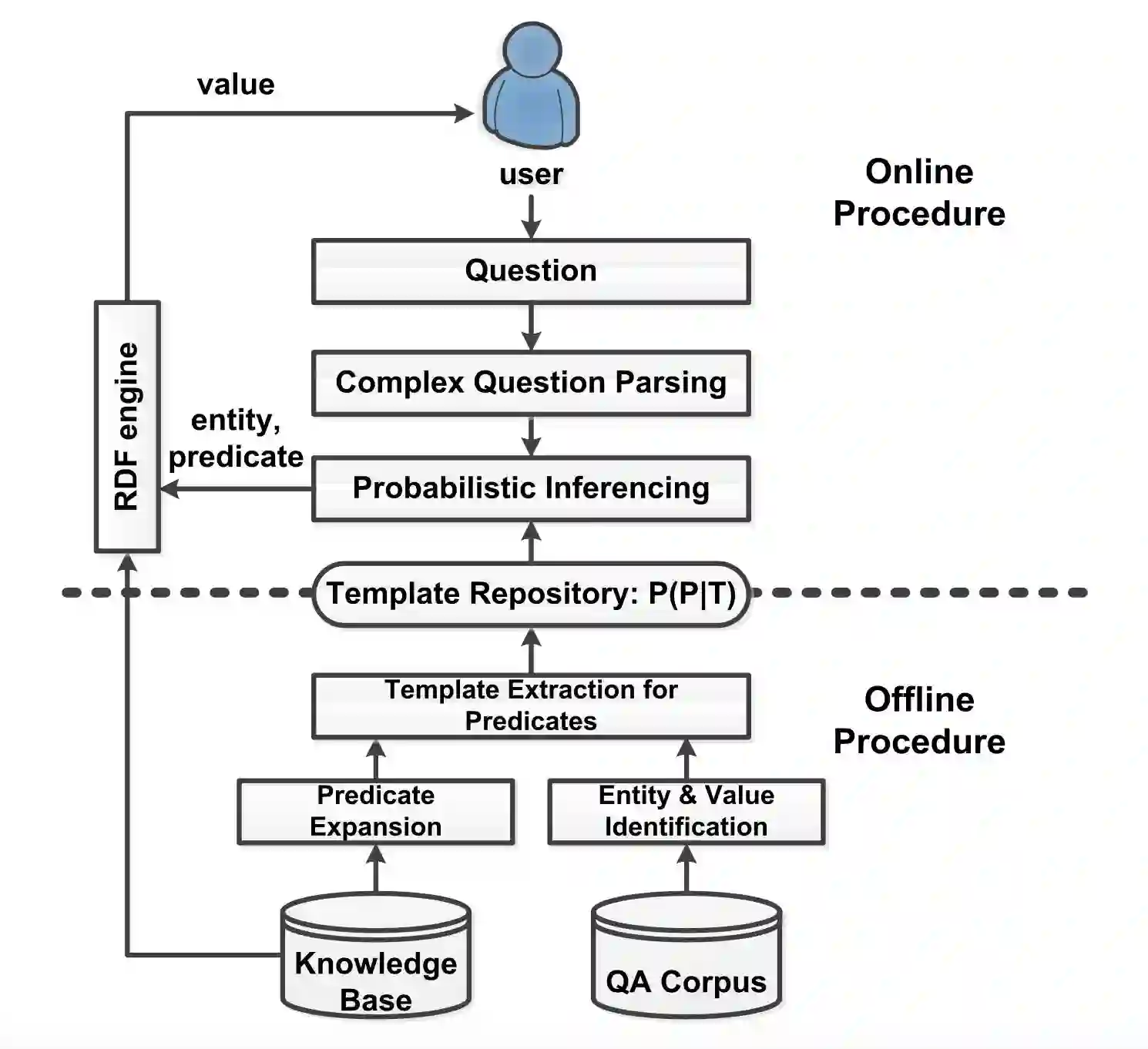
系统结构 图 8.1 展示了问答系统的流水线。它含有两个主要过程：在线 QA 部分和离线预处理部分。

在线过程：当一个问题到来，系统首先将其解析和分解为一系列二元事实型问题。这一分解过程将在第 5 节详述。对于每个二元事实型问题，系统使用概率推断来寻找它的值，如第 3 节所示。这一推断基于给定模板的属性分布，亦即 P( p|t)。这一分布是离线习得的。
离线过程：离线过程的目标是学习从模板到属性的映射，由 P(p|t) 表示。这一过程将在第 4 节详述。在第 6 节中，系统在知识图谱中扩展了属性，以学习更复杂的属性形式（例如图 1.1 中的 marriage→person→name）。

图 5.2：系统概览

第 3 节本文的方法：KBQA

第 3.1. 节在概率框架下将问题形式化。这一问题被化简为两个主要部分：离散概率计算和在线推断。第 3.2. 节中展示有关概率计算的大部分细节，但将 P(p|t) 的计算留在 4 节。第 3.3. 节将详述在线问答过程。

3.1. 问题模型

KBQA 通过 QA 语料库和知识图谱进行学习。由于问答过程的不确定性（一些问题的意图是模糊的）、不完整性（知识图谱几乎总是不完备的）和噪音（QA 语料库中的问答可能是错误的）等问题，本章为知识图谱上的问答系统构建了一个概率模型。需要强调的是从问题意图到知识图谱属性的不确定性。例如，问题 Barack Obama 来自哪里？至少与 Freebase 中的两个属性连接：“place of birth”、“place lived location”。在 DBpedia 中，谁创建了 $organization? 与属性“founder”、“father”均相关。

问题定义 5.1. 给定问题 q，问答系统的目标是寻找具有最大概率的回答 v（v 是一个简单值）：

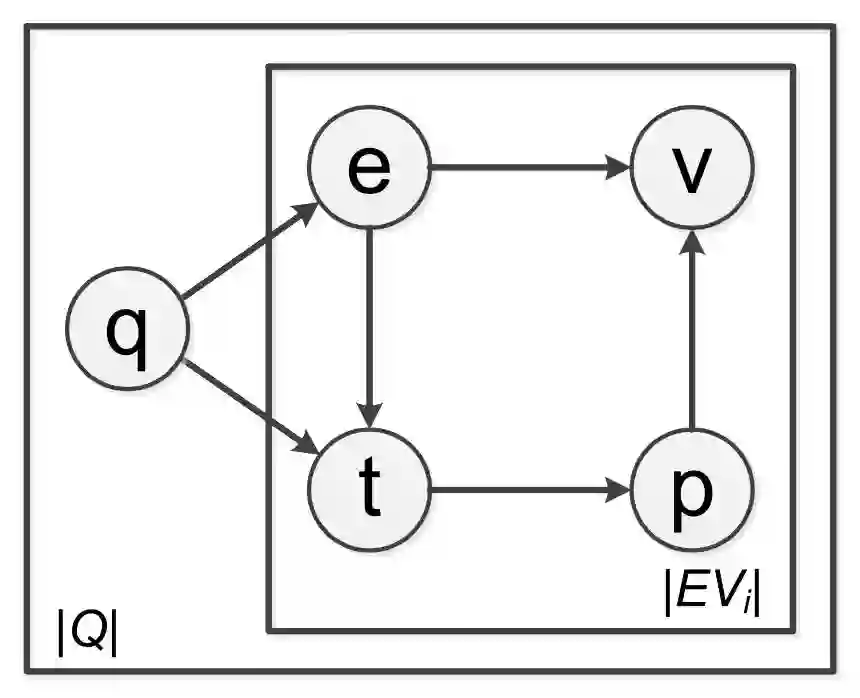
为了说明给定问题时如何寻找目标值，系统使用了一个生成模型。从用户问题 q 开始，系统首先通过其分布 P(e|q) 生成/识别它的实体 e。在得知了问题和实体之后，系统根据分布 P(t|q,e) 产生模板 t。由于属性 p 仅依赖于 t，系统可以通过 P(p|t) 来推断 p。最终，给定实体 e 和属性 p，系统通过 v 产生回答值 P(v|e, p)。v 可以被直接返回，或是嵌入一个自然语言句子作为回答。例 5.2 阐明了生成过程，并且显示了图 5.3 中随机变量的依赖关系。基于这个生成模型，可以如下计算 P(q, e, t , p, v)

现在问题 5.1 被化简为：

例 5.2. 考虑表 5.2 中（q3,a3）的生成过程。由于 q3 中的唯一实体为“Honolulu”，系统通过 P(e = d|q = q3) = 1 生成实体结点 d（见图 1.1）。通过概念化“Honolulu” 为 $city，系统生成模板 how many people are there in $city。注意到无论特指哪个城市，这一模板对应的属性总是“population”，系统通过分布 P( p|t ) 生成属性“population”。在生成实体“Honolulu” 和属性“population” 后，目标值“390k”能够轻易地从知识图谱中获取，如图 1.1 所示。最终系统使用自然语言句子 a3 作为回答。

以下小节的概要 给定了上述的目标函数，问题化简为对式 5.2 中各个概率项的计算。其中 P( p|t ) 在离线过程中计算（见第 4 节），其他全部概率项可以通过现成的解决方案（例如概念化、NER）计算。第 3.2. 将详述这些概率的计算过程。第 3.3. 节将基于这些概率结果详述在线过程。

图 5.3：概率图模型

3.2. 概率计算

在本小节中，将计算式 5.2 中除 P( p|t ) 外的各概率项。

实体分布 P(e|q) 这一分布代表从问题中辨识实体。当满足以下两个条件时，将其辨识为实体：(a)它是问题中的一个实体；(b)它在知识图谱中。对于 (a)，系统使用Stanford Named Entity Recognizer [33]。对于 (b)，系统检验实体的名字是否在知识图谱中。如果存在多个候选实体，简单地给予他们一样的概率。

系统通过 q 的回答优化离线过程中 P(e|q) 的计算。由第 4.1. 节知，系统已经从问题 qi 和回答 ai 中提取了实体-值对 EVi。假定 EVi 中的实体有相等的概率来被生成：

其中[.]是 Iverson bracket。由第7.5. 节知，这一途径比直接使用 NER 更为精确。

模板分布 P(t|q,e) 模板有类似 $person 何时出生？这样的形式。换言之，它是将一个问题中的某个实体（如“Barack Obama”）替换为实体的概念（$person）的结果。令 t = t(q,e,c) 表示模板 t 是通过将 q 中实体 e 替换为 e 的概念 c 得到的。由此可得：

其中 P(c|q, e) 是 e 在上下文 q 中的概念分布。本章的工作直接应用了[87]中的概念化方法来计算 P(c|q, e)。

值（回答）分布 P(v|e, p) 对于实体 e 和一个关于 e 的属性 p，在知识图谱中寻找属性指向的值 v 是容易的。例如，在图 1.1 所示的知识图谱中，让实体 e = Barack Obama，属性 p = dob，很容易就很能从知识图谱中得到得到 Obama 出生年份 1961。在这一例子中，P(1961|Barack Obama,dob) = 1，因为 Obama 只有一个生日。有一些属性可能有多个指向的值（例如 Obama 的孩子）。在这样的例子中，模型假定所有可能的值有相同的概率。更形式化地，可以通过如下公式计算 P(v|e, p)：

3.3. 在线过程

在这一过程中，给定用户问题 q0，系统可以通过式 5.7 计算 p(v|q0)，并且返回 argmaxv P(v|q0) 作为回答。

其中 P( p|t ) 由第 4 节所述的离线学习得到，其他概率项由第 3.2. 节所述的计算方法得到。

在线计算的复杂度：在在线计算过程中，系统依次枚举 q0 的实体、模板、属性和对应值。系统将每个问题的实体数，每个实体的概念数，每个实体-属性对的对应值数视为常量。因此在线计算过程的复杂度是 O(|P|)，由对属性的枚举而产生。这里 |P| 指知识图谱中的属性数。

第 4 节属性推断

本节介绍如何从模板中推断属性，也就是 P(p|t) 的估计值。其基本思路是将分布 P(P|T) 视作参数，然后使用极大似然 (ML) 估计法来估计 P(P|T)。第 4.1. 节介绍了基于参数估计的第一步，制定观测数据（亦即语料库中的 QA 对）的似然度。第 4.2. 和 4.3. 节分别阐述参数估计的细节以及其算法实现。

4.1. 似然度

算法的推导并不直接公式化似然概率来观察 QA 语料库 (QA )，而是先公式化一个更简单的情形——从 QA 对中提取的一个问题-实体-答案值三元组集合的似然概率。接着构造两个似然概率之间的关系。这种间接公式构造更为直接。QA 的一个回答通常是一句包括精确值和其他许多符号的复杂的自然语言。这些符号中很大一部分对于推断属性是无意义的，并且为观察带入噪音。另一方面，在生成模型中直接建立完整答案的模型比较困难，但在其中建立答案值的模型则相对简单。

接下来，第 4.1.1. 节首先从给定的 QA 对中提取实体-答案值对，从而实现对问题-实体-答案值三元组 (X) 的似然概率的公式化。然后，第 5.13 节和第 4.1.2. 节建立了 QA 语料库和 X 的似然概率之间的关系。

4.1.1. 实体-答案值提取

从答案中提取候选值的原则是一个有效实体-答案值对通常在知识图谱中存在一些一致关系。根据这个原则，可以从 (qi , ai) 中鉴别出候选实体-答案值对如下：

其中⊂表示“是......的子串”。系统支持近似匹配（比如“390K”与“395,327”匹配），从而能增加召回值。如例 5.3 所示。

例 5.3. 考虑表 5.2 中的 (q1,a1)。许多单词（例如 the，was，in）在答案中是无用的。注意到图 1.1 中，q1 中的实体 Barack Obama 与 1961 由属性“dob”连接，从而提取有效值 1961。同时要注意这步中系统也提取了噪音值 politician。下面的精炼步骤将展示如何过滤它。

EVi 的精炼在 EV(q,a) 中系统过滤了噪音对。例如例 5.3 中的（Barack Obama，politician）。直觉表明：正确值和问题应该属于同一类别。这里问题的类别表示问题的预期答案的类别。问题分类[66]已经有了相关研究。KBQA 系统使用 UIUC 分类框架[61]。并使用[66]中提出的具体分类方法。对于答案值分类，系统参考其属性的分类。属性分类是通过人工标记实现的。因为属性总共只有几千个，因此人工标记是可行的。

4.1.2. 似然函数

在实体-答案值提取后，每个 QA 对 (qi,ai) 被转移到一个问题和一个实体-答案值对集合也就是 EVi 中。假设实体-答案值对之间是独立的，观察这样的一个 QA 对的概率为：

因此，整个 QA 语料库的似然概率为：

假设每个问题都会生成一个相等的概率，也就是说 P(qi) = α，可以得到：

其中 β = αn−∑ni=1 |EVi| 被视作一个常量。式 5.11 意味着 LQA 与这些问题-实体-答案值三元组的似然概率成比例。令 X 为从 QA 语料库中提取的这类三元组集合：

令 xi = (qi,ei,vi) 来表示 X 中的一项。因而 X = {x1,...,xm}。本节建立了 QA 的似然概率与 X 的似然概率之间的线性关系。

现在，最大化 QA 的似然概率等同于最大化X的似然概率。用式 5.2 中的生成模型，通过排除所有模板 t 和属性 p 的联合概率 P(q,e,t, p,v)，模型能够计算 P(qi,ei,vi)。式 5.14 表示了这种似然概率。

4.2. 参数估计

目标：此节通过最大化式 5.14 来估计 P(p|t)。模型用参数 θ 和它对应的对数-似然概率来表示分布 P(P|T)。同时模型用 θpt 来表示概率 P(p|t)。所以下式被用来估计 θ：

其中

EM 估计的直觉：注意到一些随机变量（例如属性和模板）在概率模型中是隐藏的。这促使本章在参数估计中使用最大化期望算法来估计参数。最终目的是最大化完整数据的似然概率 L(θ)。然而，由于它包含对数求和，其计算有一定难度。因此推导转化为最大化其似然概率的下界，即 Q-函数 Q(θ;θ(s))。Q-函数的定义使用了完整数据的似然概率 Lc(θ)。EM 算法通过迭代来最大化下界 Q(θ;θ(s)) 从而最大化 L(θ)。在第 s 轮迭代中，E-步骤对每一个给定参数 θ(s) 计算 Q(θ;θ(s))；M-步骤估计能够最大化下界的参数 θ (s+1)（下一轮迭代的参数）。

完整数据的似然概率：这个函数包括对数求和，因此直接最大化 L(θ) 在计算上是很困难的。直观上来说，如果参数估计过程知道每个被观察三元组的完整数据，也就是它们是由哪个模板和属性生成的，那么估计的过程会更容易。因此对每个被观察的三元组 xi，估计过程引入一个隐藏变量 zi。zi 的值是一对属性和模板即 zi = (p,t)，用于指示 xi 是由属性 p 和模板 t 生成的。注意需要同时考虑属性和模板，因为它们在生成时不是独立的。P(zi = (p,t)) 是 xi 由属性 p 与模板 t 生成的概率。

记 Z = {z1,...,zm}。Z 和 X 一起形成完整数据。这个完整数据的对数-似然概率是:

其中

正如第 3.2. 节所讨论的， f () 可以在估计 P( p|t ) 之前被独立计算。所以它被视作一个已知的因子。

Q-函数：相比于直接优化 L(θ)，式 5.20 中定义“Q-函数”作为观察完整数据似然概率的期望。这里 θ(s) 是 θ 在迭代 s 下的估计值。根据定理 5.4，当把 h(θ(s)) 视为常量时，Q(θ;θ(s)) 为 L(θ) 提供了一个下界。因此，算法尝试去优化 Q(θ;θ(s))，而不是直接优化 L(θ)

定理 5.4（下界 [24]). L(θ) ≥ Q(θ;θ(s)) + h(θ(s)）其中 h(θ(s)) 只随 θ(s) 改变，对于 L(θ) 来说可以视作常量。

E-步骤中计算 Q(θ;θ(s))。对于式 5.20 中的每个 P(zi|X,θs)，有:

M-步骤最大化 Q-函数。通过使用拉格朗日乘子，式 5.22 计算得到 θ (s+1)。pt

4.3. 实现

本节讨论算法 5 中 EM 算法的实现。这一算法包含三步：初始化，E 步骤和 M 步骤。

初始化：为了避免式 5.21 中 P(zi = (p,t)|X,θ(s)) 为全零的情况，模型要求 θ(0) 在所有满足 f(xi,zi) > 0 的 (xi,zi) 上均匀分布。从而得到：

E步骤：这一步骤中，算法枚举所有的 zi，通过式 5.21 计算 P(zi|X,θ(s))。这一步骤的复杂度为 O(m)。

M步骤：这一步骤中，对每一个θ(s+1)Pt，算法计算 ∑m P(Zi= (p,t)|X,θ(s))。直接计算需要消耗 O(m|P||T|) 的时间，因为算法需要枚举全部可能的模板和属性。接下来，通过对每个 i 只枚举常量的模板和属性，算法的复杂度可以被减少为 O(m)。

注意到只有 P(zi = (p,t)|X,θ(s)) > 0 的 Zi 需要考虑。由式 5.19 和 5.21 可知：

由于 P(t|ei,qi) > 0，算法可以减少枚举的模板数。P(t|ei,qi) > 0 意味着算法只枚举从 qi 中的 ei 概念化过程中得到的模板。e 的概念数显然是有上界的，并且可以被看作常量。因此，第 7 行中枚举的模板 t 的总数是 O(m)。由于 P(vi|ei, p) > 0，算法可以减少枚举的属性数。P(vi|ei, p) > 0 意味着只有在知识图谱中连接 ei 和 vi 的属性需要被枚举。这样的属性数也可以被视作常量。因此 M 步骤的复杂度是 O(m) 的。

EM 算法的总体复杂度：假定整个过程重复 EM 算法 k 次，则总体复杂度为 O(km)。