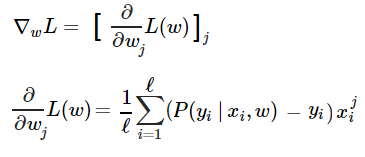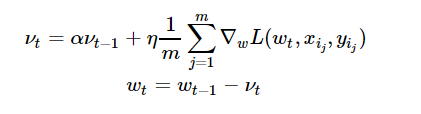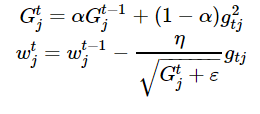课后作业（一）：如何建立一个线性分类器并进行优化

来源：sandipanweb

编译：Bot

编者按：之前，论智曾在TOP 10：初学者需要掌握的10大机器学习（ML）算法介绍了一些基础算法及其思路，为了与该帖联动，我们特从机器学习热门课程HSE的Introduction to Deep Learning和吴恩达的Neural Networks and Deep Learning中挑选了一些题目，演示Python、TensorFlow和Keras在深度学习中的实战应用.

“课后作业”第一题如何建立一个线性分类器并进行优化，来自HSE。注：本文所列代码可能并非完整答案，请参考注释思路自行尝试。

在这个任务中，我们将实现一个线性分类器，并用numpy和随机梯度下降算法对它进行训练。

二元分类

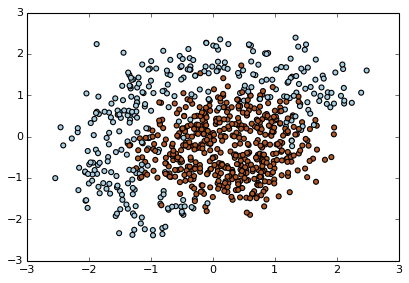
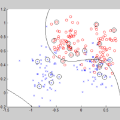
为了更直观，我们用人造数据（synthetic data）解决二元分类问题。

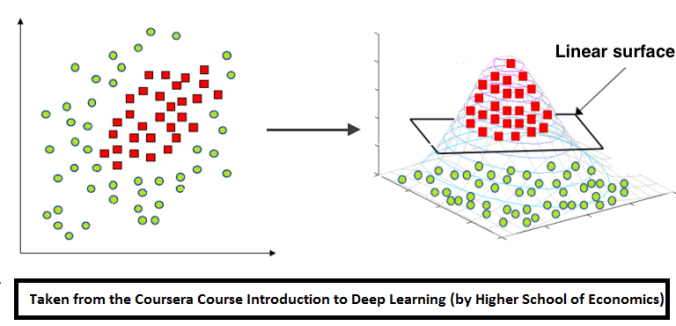
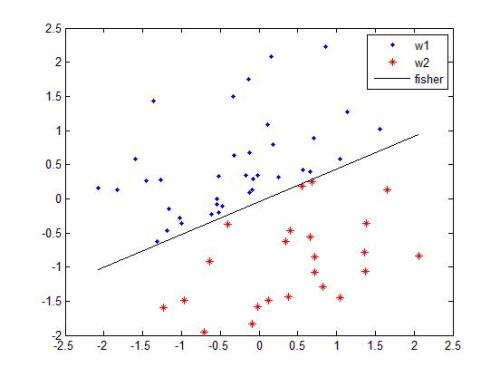
上图中有红、蓝两类数据，从分布上看它们不是线性可分的。所以为了分类，我们应该在里面添加特征或使用非线性模型。请注意，图中两类数据的决策边缘都呈圆形，这意味着我们能通过建立二元特征来使它们线性分离，具体思路如下图所示：

用expand函数添加二次函数后，我们得到了这样的测试结果：

# 简单的随机数测试
dummy_X = np.array([
        [0,0],
        [1,0],
        [2.61,-1.28],
        [-0.59,2.1]
    ])
# 调用expand函数
dummy_expanded = expand(dummy_X)
# 它应该返回这些值:   x0       x1       x0^2     x1^2     x0*x1    1
dummy_expanded_ans = np.array([[ 0.    ,  0.    ,  0.    ,  0.    ,  0.    ,  1.    ],
                               [ 1.    ,  0.    ,  1.    ,  0.    ,  0.    ,  1.    ],
                               [ 2.61  , -1.28  ,  6.8121,  1.6384, -3.3408,  1.    ],
                               [-0.59  ,  2.1   ,  0.3481,  4.41  , -1.239 ,  1.    ]])

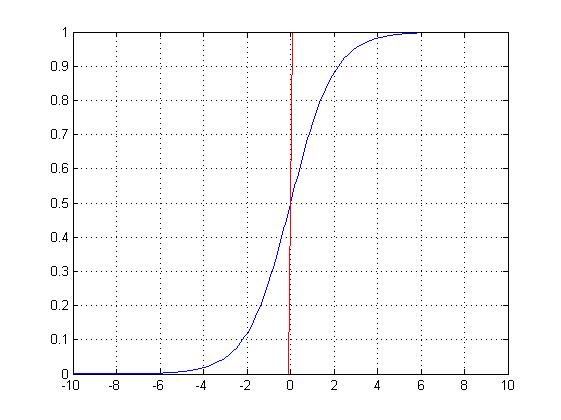
logistic回归

曾经我们提到过，logistic回归非常适合二元分类问题。为了分类对象，我们需要预测对象表示为1（默认类）的概率，这就需要用到线性模型和逻辑函数的输出：

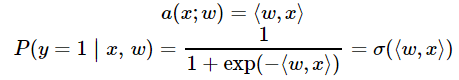
def probability(X, w):
    """
    对输入赋值特征和权值
    根据上式，返回输入x后y==1的预测概率，P(y=1|x)
    :参数 X: feature matrix X of shape [n_samples,6] (expanded) →特征矩阵X
    :参数 w: weight vector w of shape [6] for each of the expanded features →权值向量w
    :返回值: 范围在 [0,1] 之间的一系列概率.
    """
    return 1. / (1 + np.exp(-np.dot(X, w)))

在logistic回归中，我们能通过最小化交叉熵发现最优参数w：

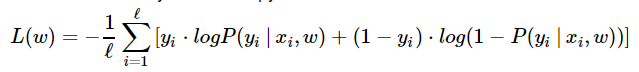
def compute_loss(X, y, w):
    """
    将特征矩阵X [n_samples,6], 目标向量 [n_samples] of 1/0,
    以及权值向量 w [6]代入上述公式, 计算标量的损失函数.
    """
    return -np.mean(y*np.log(probability(X, w)) + (1-y)*np.log(1-probability(X, w)))

由于用了梯度下降算法训练模型，我们还需要计算梯度，具体来说，就是要对每个权值的损失函数求导：

以下是具体的数学计算过程（也可点击https://math.stackexchange.com/questions/477207/derivative-of-cost-function-for-logistic-regression/2539508#2539508查看）：

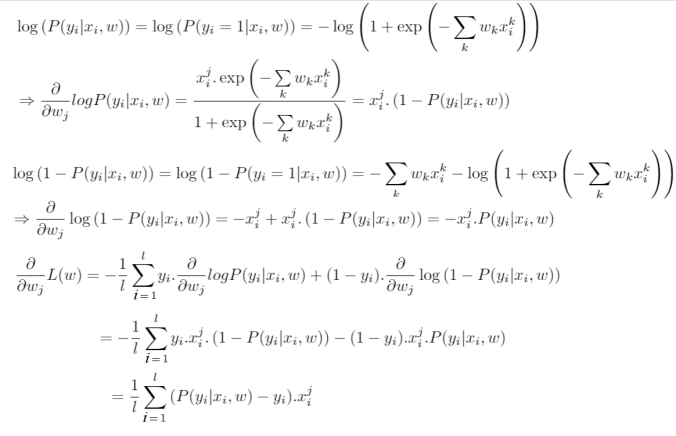
def compute_grad(X, y, w):
    """
    将特征矩阵X [n_samples,6], 目标向量 [n_samples] of 1/0,
    以及权值向量 w [6]代入上述公式, 计算每个权值的导数vector [6].
    """
    return np.dot((probability(X, w) - y), X) / X.shape[0]

训练

现在我们已经建立了函数，接下来就该用随机梯度下降训练分类器了。我们将试着调试超参数，如batch size、学习率等，来获得最佳设置。

Mini-batch SGD

不同于满梯度下降，随机梯度下降在每次迭代中只需要一个随机样本来计算其损失的梯度，并进入下一个步骤：

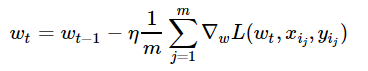
w = np.array([0, 0, 0, 0, 0, 1]) # 初始化
eta = 0.05 # 学习率
n_iter = 100
batch_size = 4
loss = np.zeros(n_iter)
for i in range(n_iter):
    ind = np.random.choice(X_expanded.shape[0], batch_size)
    loss[i] = compute_loss(X_expanded, y, w)
    dw = compute_grad(X_expanded[ind, :], y[ind], w)
    w = w - eta*dw

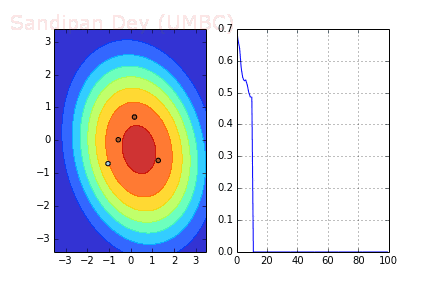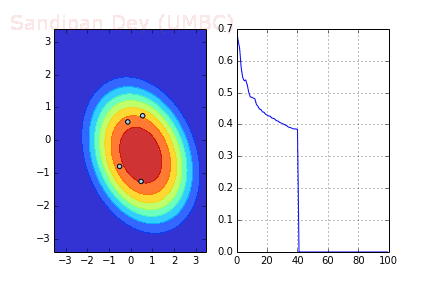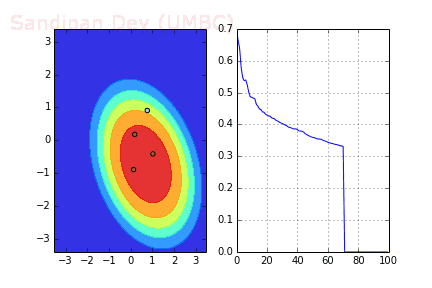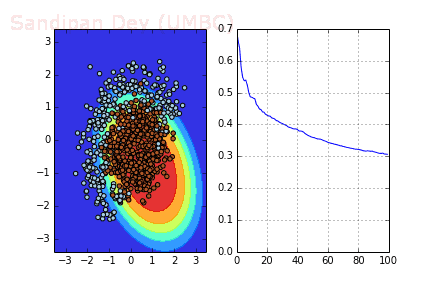
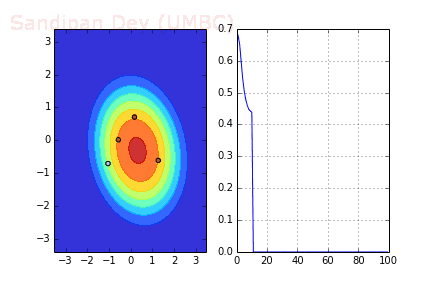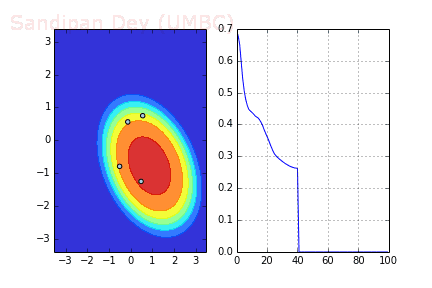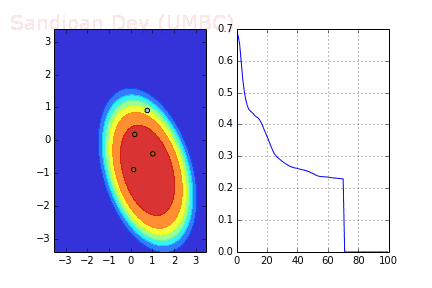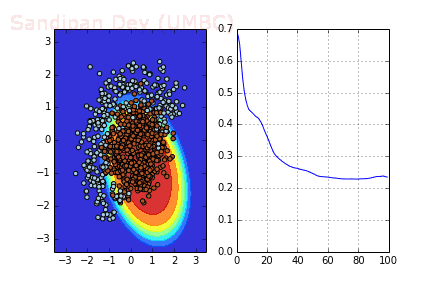
下图展示了当batch size=4时，决策面（decision surface）和交叉熵损失函数如何随着不同batch的SGD发生变化。

左：决策面；右：损失函数

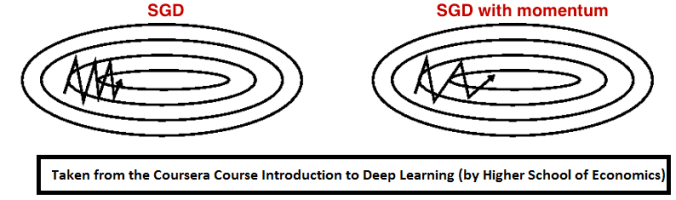
用Momentum优化SGD

Momentum是模拟物理里动量的概念，如下图所示，它能在相关方向加速SGD，抑制振荡，从而加快收敛。从计算角度说，就是对上一步骤更新向量和当前更新向量做加权平均，将其用于当前计算。

eta = 0.05 # 学习率
alpha = 0.9 # momentum
nu = np.zeros_like(w)
n_iter = 100
batch_size = 4
loss = np.zeros(n_iter)
for i in range(n_iter):
    ind = np.random.choice(X_expanded.shape[0], batch_size)
    loss[i] = compute_loss(X_expanded, y, w)
    dw = compute_grad(X_expanded[ind, :], y[ind], w)
    nu = alpha*nu + eta*dw
    w = w - nu

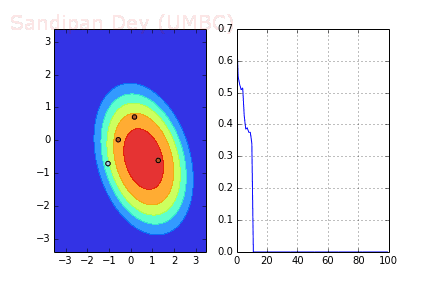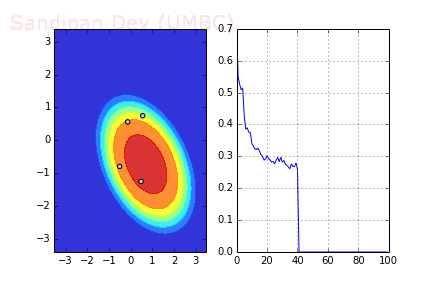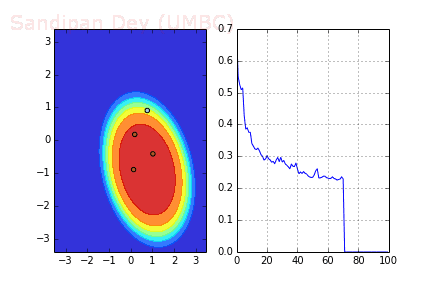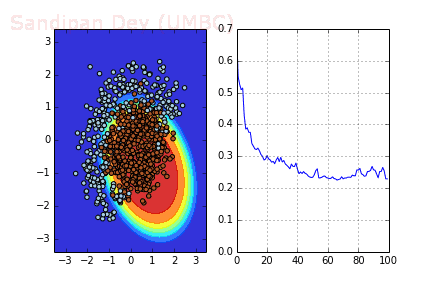
下图展示了引入Momentum后，当batch size=4时相应决策面和交叉熵损失函数随不同batch SGD+momentum发生的变化。可以看出，损失函数下降速度明显加快，更快收敛。

左：决策面；右：损失函数

RMSprop

加快收敛速度后，之后我们要做的是调整超参数学习率，这里我们介绍Hinton老爷子的RMSprop。这是一种十分高效的算法，利用梯度的平方来调整学习率：

eta = 0.05 # 学习率
alpha = 0.9 # momentum
G = np.zeros_like(w)
eps = 1e-8
n_iter = 100
batch_size = 4
loss = np.zeros(n_iter)
for i in range(n_iter):
    ind = np.random.choice(X_expanded.shape[0], batch_size)
    loss[i] = compute_loss(X_expanded, y, w)
     dw = compute_grad(X_expanded[ind, :], y[ind], w)
     G = alpha*G + (1-alpha)*dw**2
     w = w - eta*dw / np.sqrt(G + eps)

下图是使用了SGD + RMSProp后决策面和损失函数的变化情况，较之之前，函数下降更快，收敛也更快。

原文地址：sandipanweb.wordpress.com/

课程地址：www.coursera.org/specializations/aml