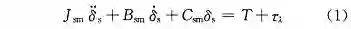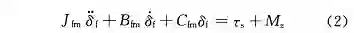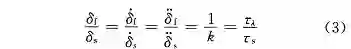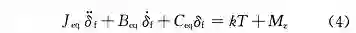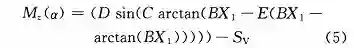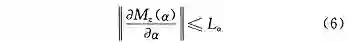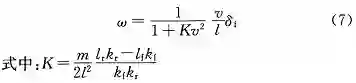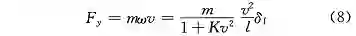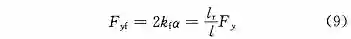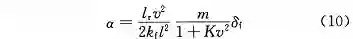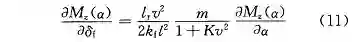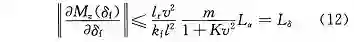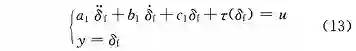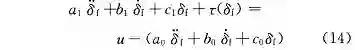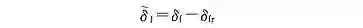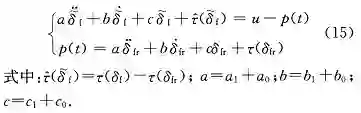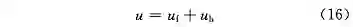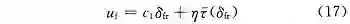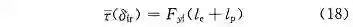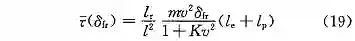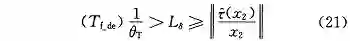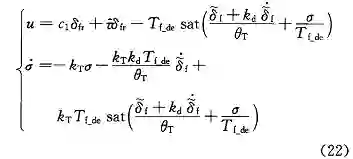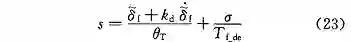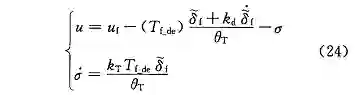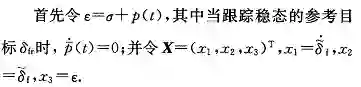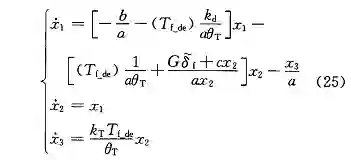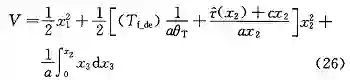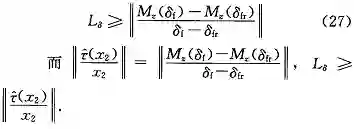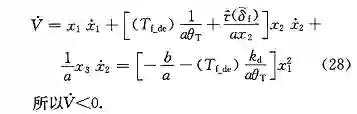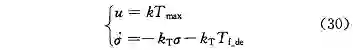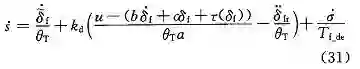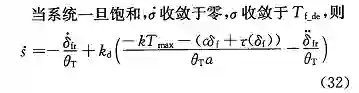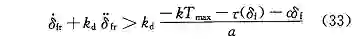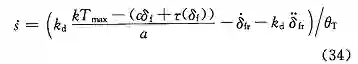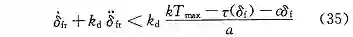考虑线控转向非线性和不确定性的转向角控制

考虑线控转向非线性和不确定性的转向角控制 | 厚势汽车

2018 年 3 月 23 日 厚势章仁燮、熊璐等

厚势按：本文研究了线控转向系统的转向轮转角跟踪控制。控制算法的设计建立在对轮胎回正力矩的非线性特性以及系统参数不确定性进行分析的基础上，并考虑了执行器力矩受限的情况。

基于一种条件积分方法，设计前馈加抗积分饱和的状态反馈控制算法来获得期望的转向轮转角。根据非线性控制理论，通过建立李雅普诺夫函数，证明线控转向控制系统的渐进稳定。最后，通过实车试验证明控制算法能够有效实现转向轮转角的精确跟踪控制。

本文来自 2017 年 2 月 23 日出版的《 同济大学学报(自然科学版) 》，作者是同济大学汽车学院的章仁燮博士、熊璐教授和李增良以及同济大学智能型新能源汽车协同创新中心的余卓平教授。

从 20 世纪 80 年代开始，线控转向系统在车辆动力学和控制领域的应用吸引相当多的科研人员进行研究。尤其是随着智能车成为近年来的研究热点，线控转向系统作为智能车重要的执行器之一，转向轮转角的控制完全通过线控来实现，因此对线控转向系统的转向轮转角控制的要求不断提高。不同于传统的转向系统，线控转向系统的转向轮转角的控制是通过连接在齿轮齿条的驱动电机实现的。因此，线控转向系统的转向轮转角控制不可避免地会受到系统参数不确定性以及轮胎非线性特性等问题的影响。

传统的 PD（Proportion Differentiation）控制技术被广泛用于使车辆方向盘转角接近期望的方向盘转角[1-3]。文献[4-5]等在 PD 控制的基础上，基于状态反馈框架，利用 LQ（Linear Quadratic）优化控制方法，使转向轮转角跟踪期望转角。虽然状态反馈控制能够保证被控状态在系统的平衡点附近保证稳定，但是不能保证系统在参数不确定的条件下，仍能使跟踪误差收敛。

Yamaguchi等 [6] 通过对前轮侧偏刚度估计，应用自适应控制的方法实现转向轮转角的跟踪控制，但是其预测估计方法是基于轮胎特性在较好线性区，没有考虑到轮胎非线性特点对回正力矩的影响。Cetin 等 [7] 和 Baviskar 等 [8] 采用了对转向机构的不确定参数进行辨识的自适应控制方法，但同样认为转向机构是线性的，因此，其在不同路况下的估计准确性有待考察。

滑模控制方法 [9-13] 被应用在线控转向系统，从其结果看，滑模控制对于参数的不确定性和路况的改变有相当的鲁棒特性，但是从试验数据可以看出电机力矩输出抖振相当明显。其次，大多数都是基于台架试验，没有考虑到实际车辆在运动过程中轮胎侧偏角对回正力矩的影响。

本文在文献 [14] 中提出的一种条件积分方法基础上，考虑到轮胎回正力矩的非线性特性以及系统参数的不确定性，设计一种前馈加抗积分饱和的状态反馈转向控制算法。其反馈增益系数的设定考虑到轮胎回正力矩的非线性特性，通过非线性控制理论的方法，建立李雅普诺夫函数，证明线控转向系统转向轮转角跟踪控制的渐进稳定。

相比滑模控制，该方法具有反馈增益较低的优点。与一般状态反馈控制相比，该方法能够避免引入积分运算而导致积分饱和引起的性能恶化，可在执行器力矩受限的条件下保证转向轮转角跟踪的稳定性。最后通过实车试验，实现了线控转向系统转向角跟踪控制。

1. 被控对象

1.1 转向系统表达式

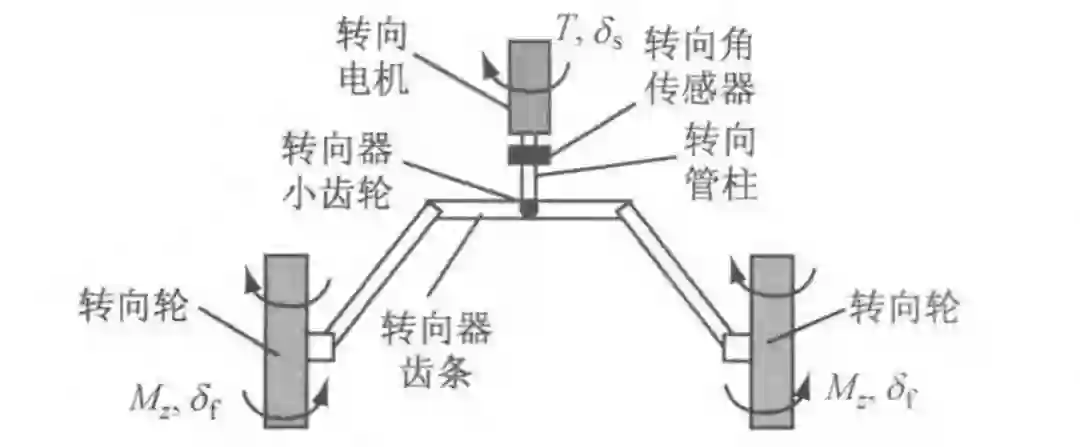
图 1 线控转向系统示意图

本文研究对象是齿轮齿条式的线控转向系统，驱动电机作用于转向管柱上，来控制转向系统转向轮转角，如图 1 所示。

首先，将驱动电机到转向器小齿轮的转向管柱系统的动力学方程表示为：

式中：J_sm 表示转向管柱系统的转动惯量；B_sm 表示转向管柱系统的阻尼；C_sm 表示转向管柱系统的刚度；τ_λ 表示转向梯形系统作用在小齿轮处的反作用力矩；T 表示位于管柱处电机的驱动力矩；δ_s 文表示转向管柱转角。

其次，将从转向器小齿轮到车辆转向轮转角的转向梯形系统的动力学方程表示为：

式中：J_fm 表示转向梯形系统的转动惯量；B_fm 表示转向梯形系统的阻尼；C_fm 表示转向梯形系统的刚度；M_z表示轮胎受到的回正力矩；δ_f 表示转向轮转角；τ_s 表示转向管柱系统作用在齿条处的作用力矩。

假设齿轮齿条之间的连接为刚性连接，可以得到转向管柱转角与转向轮转角之间的关系以及转向管柱转角速度与转向轮转角速度之间的关系：

式中：k 表示转向器的传动比。

因此通过式 (1) 和 (2) 可以得到转向系统等效动力学方程表达式：

式中：J_eq 表示转向系统等效转动惯量，J_eq = J_fm + k^2*J_sm ；B_eq 表示转向系统等效转动阻尼，B_eq = B_fm + k^2*B_sm ；C_eq 表示转向系统等效转动刚度，C_eq = C_fm + k^2*C_sm

1.2 回正力矩特性分析

1.2.1 回正力矩模型

荷兰学者 Pacejka 提出的魔术公式模型是用特殊正弦函数建立的轮胎纵向力、侧向力和回正力矩模型。基于魔术公式轮胎回正力矩的非线性表达式可以由下式得到：

式中：X_1 表示计算回正力矩的自变量，X_1 = α + S_h；口为轮胎侧偏角；α 表示曲线形状因子；D 为峰值因子，表示曲线的最大值，由轮胎的载荷决定；B 表示刚度因子，F 为回正力矩零点处的扭转刚度，则 B = F/CD，由轮胎的侧倾角和载荷决定；E 为曲率因子，表示曲线最大值附近的形状，由轮胎的侧倾角和载荷决定；S_v 表示曲线的垂直方向漂移；S_n 表示曲线的水平方向漂移。

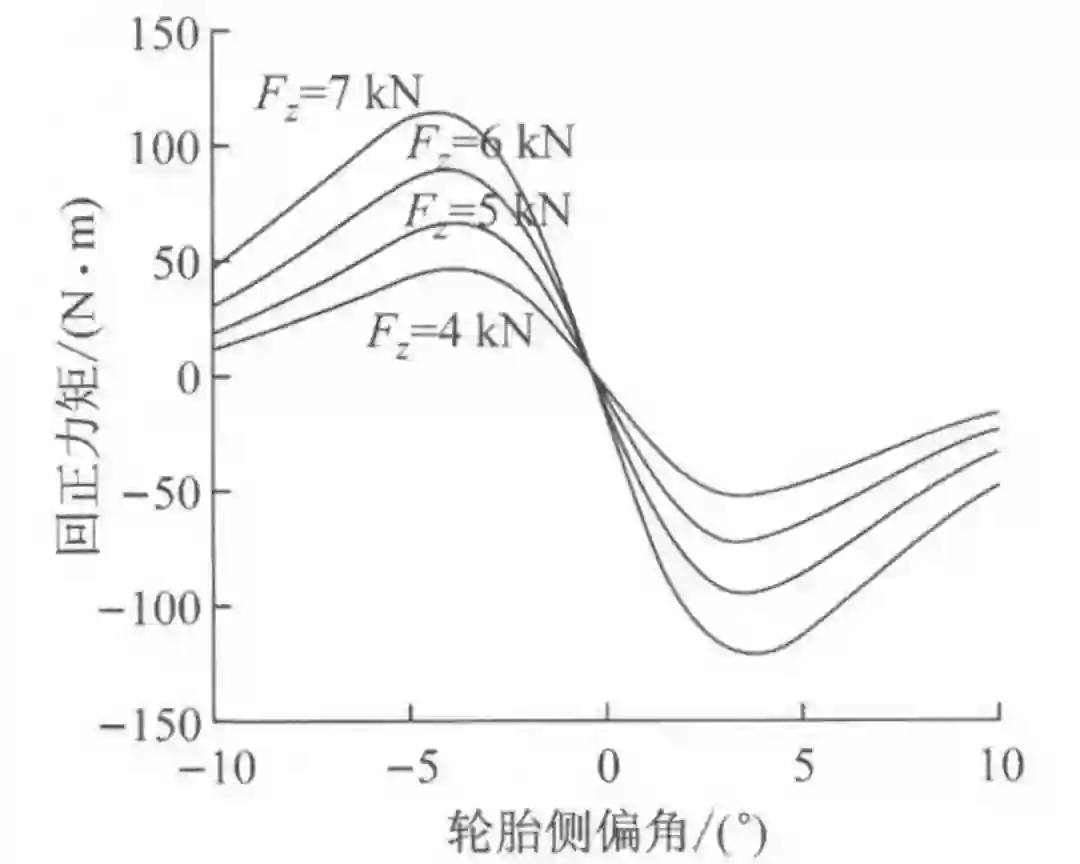
图 2 回正力矩曲线

从图 2 中可以看出，在不同垂向载荷 F_z 下车辆的回正力矩随轮胎侧偏角变化的关系。

1.2.2 回正力矩函数的利普希茨条件分析

取 α 的定义域 α ∈ (α_min，α_max)，其中，α_min 取 -10°，α_max 取 10°。

从图 2 中可以看出 M_z(α) 和 ∂M_z(α)/ ∂α 在定义域内是连续的，那么 M_z(α) 满足局部利普希茨条件：

式中：L_α 为以 α 为自变量的回正力矩函数的利普希茨常数。

根据车辆二自由度模型 [15]，得到横摆角速度 ω 与转向轮转角在稳态时的对应关系为：

v 表示车速；l 表示轴距；l_f 表示前轴距离质心的距离；l_r 表示后轴距离质心的距离；m 表示车辆整备质量；k_f 表示单个前轮的侧偏刚度；k_r 表示单个后轮的侧偏刚度。

那么得到车辆受到的侧向力与转向轮转角在稳态时的对应关系为：

根据下式可以得到转向轮受到的侧向力表达式：

结合式 (8) 和 (9) 得到前轮侧偏角 α 与转向轮转角的对应关系：

那么在给定的车辆参数下，M_z(α) 可以用 M_z(δ_f ) 表示。

进一步考虑 M_z(δ_f ) 利普希茨条件：

那么 M_z(δ_f ) 和 ∂M_z(δ_f )/∂δ_f 在定义域内同样是连续的，那么 M_z(δ_f ) 满足局部利普希茨条件。

式中，L_δ 为以 δ 为自变量的回正力矩函数利普希茨常数。

2. 控制策略

2.1 跟踪系统转变为镇定系统

根据式 (4) 得到一般非线性形式：

式中：τ(δ_f ) = -M(δ_f )；u 表示系统的控制输入，u = kT；y 表示系统的受控输出；系统参数 a_1 = J_eq，b_1 = B_eq，c_1 = C_eq。

考虑到系统参数误差，系统 (13) 转换为

式中：a_0，b_0，c_0 分别表示转向系统等效转动惯量、等效转动阻尼和等效转动刚度的测量误差，认为误差有界，|| a_0 || ≤ Δa_0，|| b_0 || ≤ Δb_0，|| c_0 || ≤ Δc_0。

使系统输出 y 跟踪期望转向轮转角输出 y_r = δ_f，定义跟踪误差为：

则跟踪系统 (14) 转变为镇定系统 (15)：

由于机械系统的固有特性，a，b，c 均大于零。

2.2 基于镇定系统 (15) 控制律设计

控制律由前馈控制律 u_f 和状态反馈的控制律 u_b 构成：

2.2.1 前馈控制律设计

首先根据系统 (15) 得到在平衡点处的前馈控制律：

式中：η ∈ [0,1]，保证 |u_f | 不超过执行器能力上限 k*T_max ；τ(δ_fr )表示稳态时的回正力矩的估计值。

根据车辆运动学特性，得到简化的回正力矩估计表达式为：

式中：l_e 表示由于主销后倾角产生的侧向作用力与主销之间的距离，记为主销后倾拖距；l_p 表示轮胎拖距；F_yf 表示转向轮受到的侧向力；轮胎拖距 [15] l_p ≈ 1/3*l_L，l_L 表示轮胎接地印迹面长度。

将式 (9) 代人式 (18) 可以得到回正力矩在平衡点处的表达式为：

从式 (17) 中可以发现 sign u_f = sign δ_fr。

2.2.2 状态反馈控制律设计

考虑到引人积分运算时，系统受到外部干扰，建模不精确以及执行器力矩受限等因素影响，长时间无法镇定系统会导致积分运算不断增大，从而导致控制算法失效，进一步损害系统瞬态响应甚至是稳定性。因此，状态反馈控制律的设计是基于一种条件积分方法 [14]。

其次，考虑到控制量 u 的取值范围 -k*T_min ≤ u ≤ -k*T_max 。T_max 表示电机受限的最大驱动力矩，以及时变反馈系数和时变前馈对积分运算的影响。

要保证系统的渐进稳定，钟取值要满足以下条件：

其中，L_δ 是函数 M_z(δ_f) 的利普希茨常数。

因此，基于前馈控制律 (17) 和反馈控制律 (20)，控制律 (16) 可以表示为：

2.3 线控转向系统稳定性分析

条件积分方法其本质是为防止积分运算饱和的状态反馈控制。因此系统稳定性将从积分运算未饱和、饱和两方面进行分析。

首先令

2.3.1 积分运算未饱和

当积分运算未饱和，| s | < 1。所设计的控制律为引人积分项的状态反馈控制，能够保证系统的状态 δ_f 被镇定到原点。

控制律 (22) 可被转换为：

（1）系统方程变换

再将控制律 (24) 代人系统 (15)，系统 (15) 可转换为状态空间：

（2）系统渐进稳定证明

利用非线性控制理论的方法建立李雅普诺夫函数，证明系统 (25) 渐进稳定。

① 建立李雅普诺夫函数

根据式 (12)，由于 M_z(x_2) 满足利普希茨条件，所以

因此当满足 T_(f_de)/θ_T ＞L_δ ，则 V ＞ 0。

② 证明李雅普诺夫函数一阶导数小于零

对式 (26) 求一阶导数得到李雅普诺夫函数的变化率：

因此，系统 (25) 渐进稳定，保证 δ_f 收敛到零。

2.3.2 积分运算饱和

当积分运算饱和，即 | s | ≥ 1。系统的稳定性需要满足以下两点要求：

（1）积分运算不发散，保证系统仍然稳定。

从式 (29) 可以发现控制量达到执行器所能达到的最大限制值时，σ 值会收敛于 T_(f_de)，保证原有的积分值稳定不发散。

同理当 s ≤ -1 时，控制律 (20) 转换为

σ 值会收敛于 -T_(f_de)。

（2）满足一定条件下能使 | s | 在有限时间内收敛到 (-1,1) 范围内，恢复到非饱和状态，保证系统渐进稳定。

以 s ≥ 1 为例，只要使 s 的导数 < 0 就可以保证 s 在有限时间内收敛到 (0,1) 范围内。

对式 (23) 求导，并代人表达式 (14) 可以得到 s 的导数表达式：

所以要使 s 的导数表 < 0，需满足

则 s 会收敛到 (0,1) 内，使转向轮转角跟踪误差收敛到零。

同理当 s ≤ -1，当系统一旦饱和

使 s 的导数 > 0，就可以保证 s 在有限时间内收敛到 (-1,0) 范围内，那么需满足：

因此当满足式 (32) 和式 (35) 时，s 则又重新收敛到 (-1,1) 范围，恢复非饱和状态。

3. 仿真试验

仿真试验是在软件 Simulink 环境下通过搭建转向系统模型实现的。同样的实车参数被用于仿真试验，车辆参数见表 1 所示。

在仿真试验中，将基于条件积分方法的前馈加抗积分饱和的状态反馈控制算法与滑模控制进行对比分析。试验工况为在车速 60 km/h 下，期望转向轮转角为 2° 的阶跃工况。

表 1 车辆参数

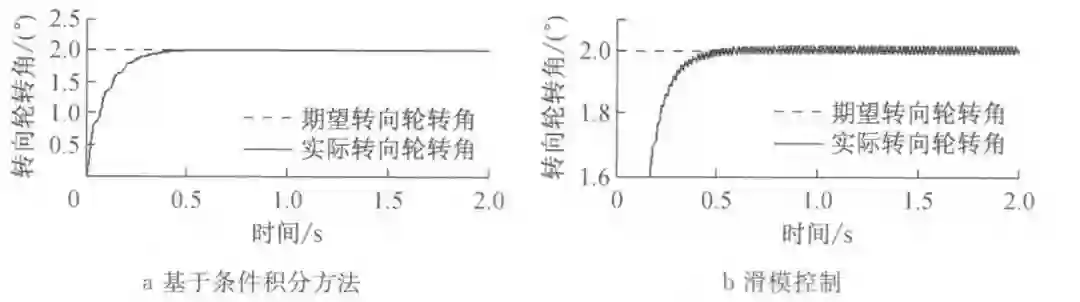
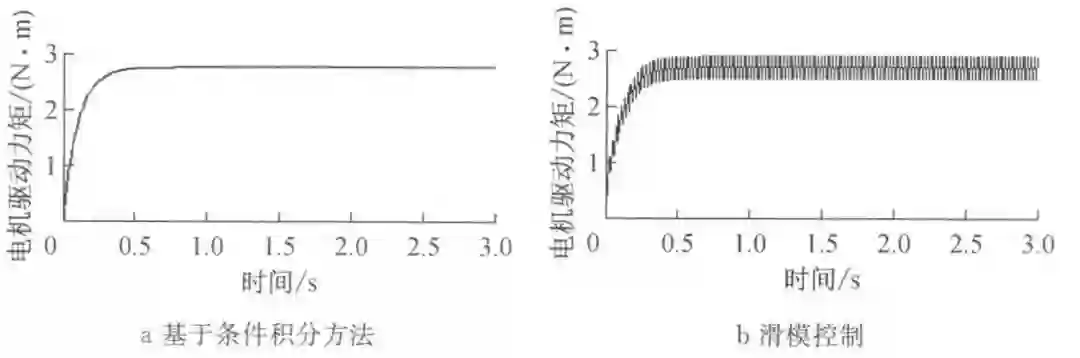
图 3 和图 4 分别表示基于条件积分方法的前馈加抗积分饱和的状态反馈控制算法和滑模控制算法的转向角跟踪控制效果，以及其电机驱动力矩控制值。

图 3 转向角跟踪示意图

对比图 3a 和图 3b 可以发现，两种控制算法的控制精度相差不大。但是当基于滑模控制算法时，转向轮转角在期望值附近波动比较大。

图 4 电机驱动力矩示意图

同时根据图 4a 和图 4b 中电机驱动力矩的对比也可以发现，当基于滑模控制算法时，电机驱动力矩波动比较大。对于转向系统而言，转向轮转角的波动会影响驾驶和乘坐感觉，电机驱动力矩的频繁波动会影响电机的寿命。

因此从图 3a 和图 4a 可以看出，基于条件积分方法的前馈加抗积分饱和的状态反馈控制算法在满足精度的同时，能平滑地实现转向轮转角的跟踪控制。

4. 实车试验

图 5 试验平台示意图

转向轮转角跟踪控制的试验平台是基于如图 5a 所示的轮毂/轮边电驱动汽车平台的EPS（Electric Power Steering）实现转角控制。通过发送需求力矩给助力电机控制器，使助力电机产生相应的力矩。控制器参数见表 2。

表 2 控制器参数

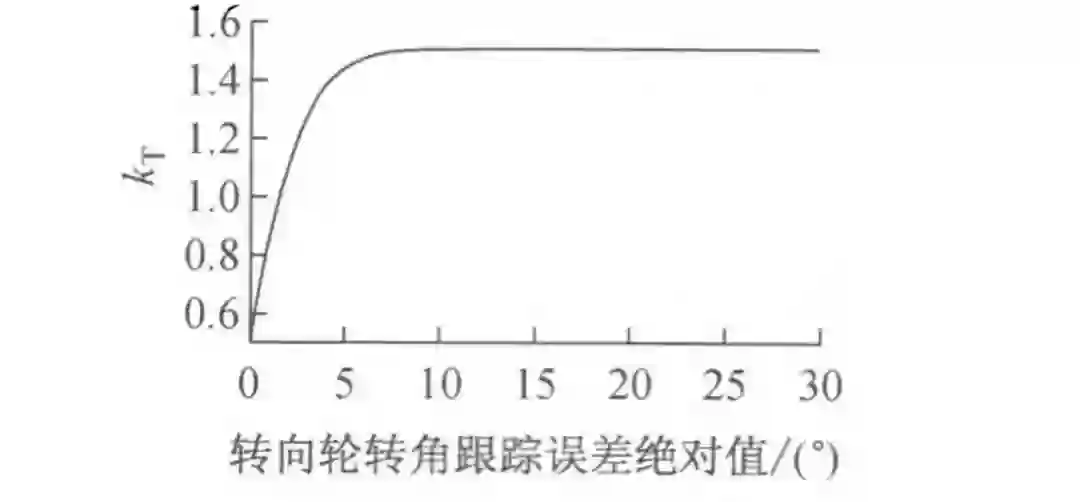
为防止有过大的超调量出现，根据转向轮转角跟踪误差的绝对值来改变是 T 的取值，是 T 的取值随跟踪误差的绝对值增大而增大直到 1.5 为止，如图 6 所示。

图 6 k_T 取值示意图

为考察线控转向系统的稳态跟踪特性和瞬态跟踪特性，设计了原地转向角跟踪，稳态圆周工况以及蛇形工况：

原地转向角跟踪和稳态圆周工况以线控转向系统跟踪期望转向轮转角的稳态误差和上升时间为评价标准；
蛇形工况以实际转向轮转角最大幅值除以期望转向轮转角最大幅值的幅频特性和实际转向轮转角相位减去期望转向轮转角相位的相频特性为评价标准。

4.1 原地转向角跟踪

相比行驶时转向轮受到的回正力矩主要由侧向力产生，原地转向时回正力矩主要由轮胎与地面的摩擦阻力矩产生，故将原地转向角跟踪试验独立进行。试验过程中期望转向轮转角每 5° 一次阶跃直到 20°。

图 7 原地转向角跟踪示意图

车速为零的情况下，由于回正力矩由摩擦阻力产生，无法估计得到，因此回正力矩误差完全通过积分补偿，会产生一定超调和滞后，但是由于车速为零，对实时性要求不高，这时更关注稳态误差。从图 7 可以看出，其平均稳态误差仍为 0.1°，平均上升时间为 0.8 s。因此通过试验证明线控转向系统能够准确地跟踪稳态的期望转向轮转角。

4.2 稳态圆周工况

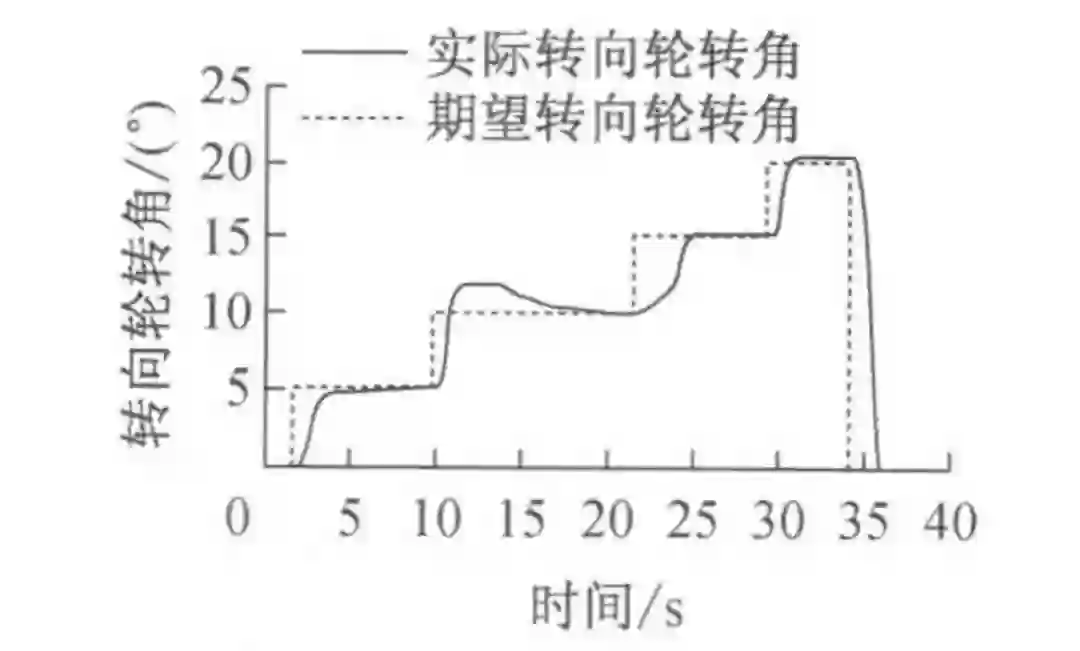
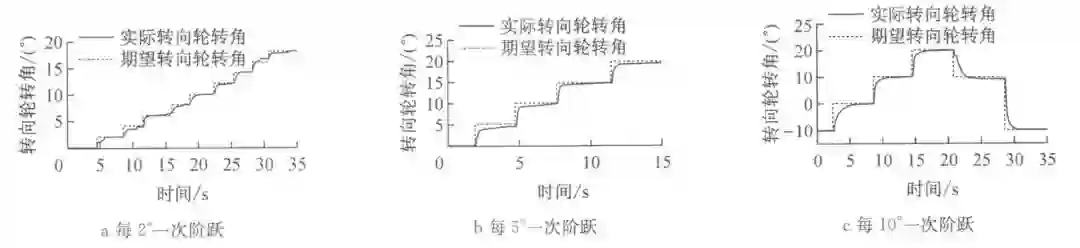
由于试验场地原因，车速在 20 km/h 左右。试验中期望转向轮转角为每 2° 一次阶跃直到 20°，见图 8a；每 5° 一次阶跃直到 20°，见图 8b；每 10° 一次阶跃直到 20°，见图 8c。

图 8 稳态圆周工况转向角跟踪示意图

图 8 分别验证了线控转向系统跟踪小角度和大角度阶跃信号的稳态跟踪能力。其平均稳态误差为 0.1°，平均上升时间为 0.3 s。因此，通过试验证明线控转向系统能够准确并快速地跟踪稳态的期望转向轮转角。

4.3 蛇形工况

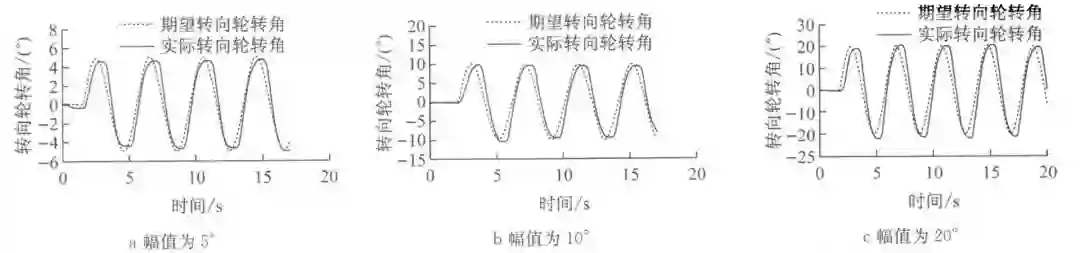
图 9 周期为 4 s 蛇形工况转向角跟踪示意图

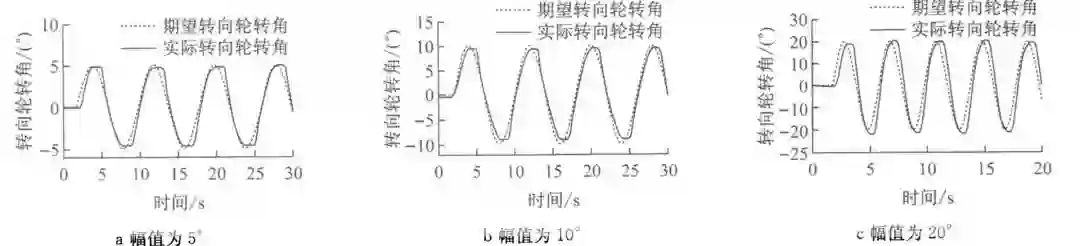
由于试验场地原因，车速在 20 km/h 左右。试验中期望转向轮转角周期为 4 s（见图 9），幅值分别为 5°（见图 9a），10°（见图 9b），20°（见图 9c）的正弦信号；期望转向轮转角周期为 8 s（见图 10），幅值分别为 5°（见图 10a），10°（见图 10b），20°（见图 10c）的正弦信号。

图 10 周期为 8 s 蛇形工况转向角跟踪示意图

图 9 相比图10验证了相同幅值、不同频率下线控转向系统对期望转向轮转角的瞬态跟踪能力。而两者各自又验证了相同频率、不同幅值的瞬态跟踪能力。其平均幅频特性为o。95，平均相频特性为一o。312 58 rad。因此，通过试验证明了线控转向系统能够快速地跟踪时变的期望转向轮转角。

5. 总结

（1）基于魔术公式轮胎模型，对轮胎回正力矩的非线性特性进行了理论分析。

（2）基于回正力矩的非线性特性和系统参数不确定性，设计了前馈加状态反馈的控制律。基于一种条件积分方法，防止由于状态反馈引人了积分运算，在执行器力矩受限的情况下，导致积分饱和引起的性能恶化，保证转向轮转角跟踪的稳定性。

（3）通过仿真试验，证明所设计的控制算法在满足精度的同时，能平滑地实现转向轮转角的跟踪控制。通过实车试验考察了线控转向系统的稳态跟踪特性和瞬态跟踪特性。实车试验结果证明，通过所设计的控制算法，线控转向系统能够准确并快速地跟踪期望的转向轮转角。

参考文献

[1] Bertoluzzo M，Buja G，Menis R .Contr o1 schemes for steer-by wire systems [J] .IEEE Industrial Electronics Magazine，2006，1(1)：20

[2] Kim C J，Jang J H，Oh S K，et al. Development of a control algorithm for a rack-actuating steer-by-wire system using road information feedback [J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering，2008，222(9)：1559

[3] Setlur P，Wagner J R，Dawson D M，et al. A trajectory tracking steer-by-wire control system for ground vehicles[J] . IEEE Transactions on vehicular Technology，2006，55(1)：76

[4] Marumo Y，Nagai M . Steering control of motorcycles using steer-by-wire system[J] .Vehicle System Dynamics，2007，45 (45)：445

[5] Yoshitaka M，Nozomi K . Control effects of steer-by-wire system for motorcycle on lane-keeping performance [J]. Vehicle System Dynamics，2 o11，49(8)：1283

[6] Yamaguchi Y，Murakarlli T . Adaptive contro for virtual steering characteristics on electric vehicle using steer-by-wire system [J]. IEEE Transactions on Industrial Electronics，2009，56(5)：1585

[7] Cetin A E，Adli MA，Barkana DE，et al. Implementation and development of an adaptive steering-control system [J]. IEEE Transactions on Vehicular Technology，2010，59(1)：75

[8] Baviskar A，Wagner J R，Dawson D M，et al. An adjustable steer-by-wire haptic-interface tracking controller for ground vehicles [J]. IEEE Transactions on Vehicular Technology，2009，58(2)：546

[9] Wang H，Man Z，Kong H，et al. Terminal sliding mode control for steer-by-wire system in electric Vehicles[C]. //Industrial Electronics and Applications. Singapore：IEEE，2012：919-924

[10] Wang H，Kong H，Man Z，et al. Sliding mode control for steer-by-wire systems with AC motors in road vehicles [J]. IEEE Transactions on Industrial Electronics，2014，61(3)：1596

[11]Wang H，Man Z，Shen W，et al. Robust sliding mode control for steer .by-wire systems with AC motors in road vehicles[C]. // Industrial Electronics and Application. Melbourne：IEEE，2013：674-679

[12] Kazemi R，Janbakhsh A A. Nonlinear adaptive sliding mode control for vehicle handling improvement via steer-by-wire [J] . International Journal of Automotive Technology，2010，11(3)： 345

[13]Do M T，Man Z，Zhang C，8t of .Robust sliding mode-based learning control for steer-by-wire systems in modern vehicles [J]. Vehicular Technology IEEE Transactions on，2014，63 (2)：580

[14] Kay H S，Khalil H K .Universal controllers with nonlinear integrators[C] // Proceedings of the American Control Conference. Alaska：IEEE，2002：116-121

[15] Mitschke D I M. Dynamik der kraftfahrzeuge [M]. Berlin: Springer-Verlag，1984

编辑整理：厚势分析师拉里佩

转载请注明来自厚势和厚势公号：iHoushi

-END-

文章精选

企业家

马斯克和贾跃亭｜福特CEO下台｜正道汽车仰融

任正非裁员｜电池大牛凯尔提离开特斯拉

智能驾驶

BBC自动驾驶纪录片｜自动驾驶第一案，谷歌讼Uber

为什么说百度阿波罗画虎不成反类犬？

基于线控制动系统的车辆横摆稳定性优化控制