差分隐私保护：从入门到脱坑

2018 年 9 月 10 日 FreeBuf

差分隐私（Differential Privacy）是密码学中的一种手段，旨在提供一种当从统计数据库查询时，最大化数据查询的准确性，同时最大限度减少识别其记录的机会。简单地说，就是在保留统计学特征的前提下去除个体特征以保护用户隐私。

0x00 背景

随着数据挖掘技术的普遍应用，一些厂商通过发布用户数据集的方式鼓励研究人员进一步深入挖掘数据的内在价值，在数据集发布的过程中，就存在安全隐患，可能导致用户隐私的泄露。2016年欧盟通过《一般数据法案》（General Data Protection Regulation, GDPR），规定了个人数据保护跨越国界，明确了用户对个人数据的知情权和被遗忘权。数据集中通常包含着许多个人的隐私数据，例如医疗诊断记录、个人消费习惯和使用偏好等，这些信息会由于数据集的发布而泄露。尽管删除数据的身份标识符（例如姓名、ID号等）能够在一定程度上保护个人隐私，但是以下案例表明，这种操作并不能保证隐私信息的安全性。

2006年10月，Netflix提出一笔100万美元的奖金，作为将其推荐系统改进达10%的奖励。Netflix还发布了一个训练数据集供竞选开发者训练其系统。在发布此数据集时，Netflix提供了免责声明：为保护客户的隐私，可识别单个客户的所有个人信息已被删除，并且所有客户ID已用随机分配的ID[sic]替代。由于Netflix不是网络上唯一的电影评级门户网站，其他网站还有很多，包括IMDb。个人可以在IMDb上注册和评价电影，并且可以选择匿名化自己的详情。德克萨斯州大学奥斯汀分校的研究员Arvind Narayanan和Vitaly Shmatikov将Netflix匿名化的训练数据库与IMDb数据库（根据用户评价日期）相连，能够部分反匿名化Netflix的训练数据库，危及到部分用户的身份信息。[1]

此外，卡内基梅隆大学的Latanya Sweeney的将匿名化的GIC数据库（包含每位患者的出生日期、性别和邮政编码）与选民登记记录相连后，可以找出马萨诸塞州州长的病历。[2]

差分隐私是Dwork在2006年针对统计数据库的隐私泄露问题提出的一种新的隐私定义。在此定义下，对数据库的计算处理结果对于具体某个记录的变化是不敏感的，单个记录在数据集中或者不在数据集中，对计算结果的影响微乎其微。所以，一个记录因其加入到数据集中所产生的隐私泄露风险被控制在极小的、可接受的范围内，攻击者无法通过观察计算结果而获取准确的个体信息。[3,4]

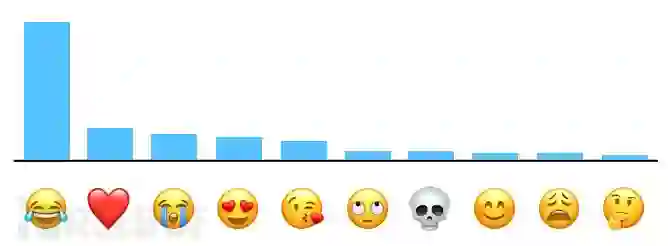
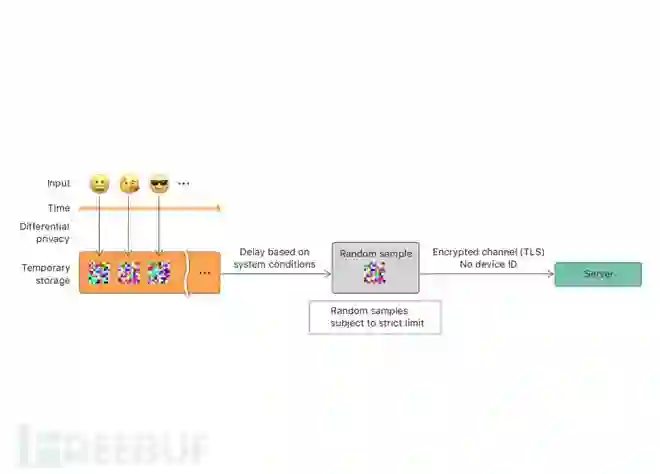
目前，一些企业已经开展了相关的工程实践。Google利用本地化差分隐私保护技术从Chrome浏览器每天采集超过1400万用户行为统计数据。[5]在2016年WWDC主题演讲中，苹果工程副总裁Craig Federighi宣布苹果使用本地化差分隐私技术来保护iOS/MacOS用户隐私。根据其官网披露的消息，苹果将该技术应用于Emoji、QuickType输入建议、查找提示等领域。例如，Count Mean Sketch算法（CMS）帮助苹果获得最受欢迎的Emoji表情用来进一步提升Emoji使用的用户体验，图1展示了利用该技术获得的US English使用者的表情使用倾向。图2展示了该技术的具体流程。

图1

图2

0x01 形式化定义

基本定义

对于一个有限域Z，z∈Z为Z中的元素，从Z中抽样所得z的集合组成数据集D，其样本量为n，属性的个数为维度d。

对数据集D的各种映射函数被定义为查询（Query），用F={f1, f2, ······}来表示一组查询，算法M对查询F的结果进行处理，使之满足隐私保护的条件，此过程成为隐私保护机制。

设数据集D与D’，具有相同的属性结构，两者的对称差记作DΔD’，|DΔD’|表示DΔD’中记录的数量。若|DΔD’|=1，则称D和D’为邻近数据集。

差分隐私

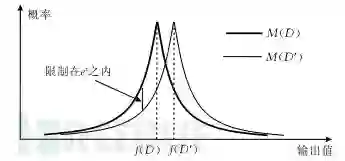
设有随机算法M，PM为M所有可能的输出构成的集合。对于任意两个邻近数据集D和D’以及PM的任何子集SM，若算法M满足：Pr[M(D)∈SM]<=exp(ε)*Pr[M(D’)∈SM]，则称算法M提供ε-差分隐私保护，其中参数ε称为隐私保护预算。

其中，Pr[]表示发生某一事件的概率。如图1所示，算法M通过对输出结果的随机化来提供隐私保护，同时通过参数ε来保证在数据集中删除任一记录时，算法输出统一结果的概率不发生显著变化。

图3

实现机制

在实践中，通常使用拉普拉斯机制（Laplace Machanism）和指数机制（Exponential Mechanism）来实现差分隐私保护。其中，拉普拉斯机制用于数值型结果的保护，指数机制用于离散型结果的保护。

拉普拉斯机制

拉普拉斯机制通过向确切的查询结果中加入服从拉普拉斯分布的随机噪声来实现ε-差分隐私保护。记位置参数为0、尺度参数为b的拉普拉斯分布为Lap(b)，那么其概率密度函数为:p(x)=exp(-|x|/b)/2b，

对于拉普拉斯机制，我们进行以下定义：给定数据集D，设有函数f：D->Rd，其敏感度为Δf，那么随机算法M(D)=f(D)+Y提供ε-差分隐私保护，其中Y~Lap(Δf/ε)为随机噪声，服从尺度参数为Δf/ε的拉普拉斯分布。

指数机制

由于拉普拉斯机制仅适用于数值型结果，在一些特定场景中，往往需要返回离散型结果，例如某一方案或某一实体等。对此，McSherry等人提出了指数机制。

设查询函数的输出域为Range，域中的每个值r∈Range为一实体对象。在指数机制下，函数q(D,r)->R成为输出值r的可用性函数，用来评估输出值r的优劣程度。

对于指数机制，我们进行以下定义：设随机算法M输入为数据集D，输出为一实体对象r∈Range，q(D,r)->R为可用性函数，Δq为函数q(D,r)->R的敏感度。若算法M以正比于exp(εq(D,r)/2Δq)的概率从Range中选择并输出r，那么算法M提供ε-差分隐私保护。

组合性质

性质1

假设有n个随机算法K，其中Ki满足εi-差分隐私，则{Ki}（1<=i<=n）组合后的算法满足sum(εi)-差分隐私。

性质2

设有n个随机算法K，其中Ki满足εi-差分隐私，且任意两个算法的操作数没有交集，则{Ki}（1<=i<=n）组合后的算法满足max(εi)-差分隐私。

0x02 实例

拉普拉斯机制

ID	hasCancer
01	Yes
02	No
03	Yes
04	No
···	···

我们设上述数据集为D，用于统计个体是否患有癌症。以计数函数为例，即count(D)函数，用于表示数据集D中共有n条hasCancer属性值为Yes的数据，即该数据集中共有n人患有癌症，该函数的敏感度为1，具体计算方法可参考相关论文。

为了方便计算，我们假设此时的隐私预算ε为1，则Δf/ε=1，即返回结果为count(D)+Lap(0,1)。

import numpy as np
loc, scale = 0., 1.
s = np.random.laplace(loc, scale, 1)
result= realResult + s[0]
print result

import numpt as np
import matplotlib.pyplot as plt
loc, scale = 0., 1.
s = np.random.laplace(loc, scale, 1000)
result_list = list(map(lambda x : x+50,s))
plt.hist(result_list, 30, density=True)
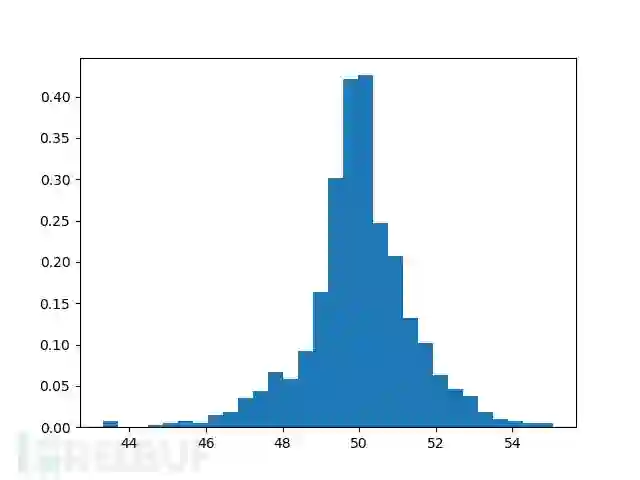
plt.show()

假设在上述数据集中，count(D)的真实结果为50，图4展示了重复1000次后的结果分布，基本符合拉普拉斯分布。

图4

指数机制

ID	disease
01	Cancer
02	HIV
03	HIV
04	HPV
···	···

我们设上述数据集为D，用于统计个体所患疾病的种类，为了方便计算，我们假定上述数据集中disease属性仅有三种类型，即Cancer、HIV和HPV。现在希望能够获得患者最多的疾病类型。在该场景下，可用性函数q(D, r)为数据集D中疾病r的患者数目，显然该函数Δq=1。

disease	可用性
Cancer	50
HIV	20
HPV	30

为了方便计算，我们假设此时的隐私预算ε为1。

disease	exp(εq(D,r)/2Δq)	概率
Cancer	exp(25)	0.9999
HIV	exp(10)	3*10^-7
HPV	exp(15)	0.00004

为了比较不同隐私预算ε的影响，我们进一步比较隐私预算ε分别取值为0，0.1和0.5时的情况。

disease	ε=0	ε=0.1	ε=0.5
Cancer	0.333	0.628	0.993
HIV	0.333	0.124	0.006
HPV	0.333	0.231	0.001

上述结果也验证了我们的结论，即隐私预算ε越大，数据可用性越高，安全性越低，当隐私预算ε=0时，数据失去意义。

0x03 总结

上面只是差分隐私保护的简单应用，要想应用在生产环境中，还需要针对具体场景对算法进一步改造，但差分隐私保护的思想是不变的。差分隐私提供针对隐私保护的方法提供了形式化的定义，让信息安全人员和数据管理员对当前环境中的隐私保护情况有一个可量化的指标。另外，差分隐私提供了一种无关攻击者背景知识的数据保护方案，相比k-anonymity、l-diversity和t-closeness等方法更具优势。

在早期，人们很难证明我的方法保护了隐私，更无法证明究竟保护了多少隐私。现在差分隐私用严格的数学证明告诉人们，只要你按照我的做，我就保证你的隐私不会泄露。[6]

在这个意义上，差分隐私的出现可以说是具有重大意义的，它将隐私保护这一工程问题进行抽象，变为数学问题，

本文介绍了中心化的差分隐私方法，引出了主流的拉普拉斯机制和指数机制，关于机制实现ε-差分隐私保护的数学证明，可以在文章差分隐私若干基本知识点介绍（一）和差分隐私若干基本知识点介绍（二）中获得，其中的数学知识基本在高中范围。

而背景介绍中Google、苹果等公司采用的本地化差分隐私方法，是差分隐私保护的另一分支，在本地化差分隐私中，由于没有全局敏感度的概念，因此本文介绍的拉普拉斯机制和指数机制不再适用，大多数方案采用随机响应机制，如果可能将在后期的文章中介绍。

参考文献

[1] Narayanan, Arvind, and Vitaly Shmatikov. “Robust de-anonymization of large sparse datasets.” Security and Privacy, 2008. SP 2008. IEEE Symposium on. IEEE, 2008.

[2] De Montjoye, Yves-Alexandre, et al. “Unique in the crowd: The privacy bounds of human mobility.” Scientific reports 3 (2013): 1376.

[3] Dwork, Cynthia. “Differential privacy: A survey of results.” International Conference on Theory and Applications of Models of Computation. Springer, Berlin, Heidelberg, 2008.

[4] 熊平, 朱天清, and 王晓峰. “差分隐私保护及其应用.” 计算机学报 37.1 (2014): 101-122.

[5] Erlingsson, Úlfar, Vasyl Pihur, and Aleksandra Korolova. “Rappor: Randomized aggregatable privacy-preserving ordinal response.” Proceedings of the 2014 ACM SIGSAC conference on computer and communications security. ACM, 2014.

[6] Nemo “苹果的 Differential Privacy 差分隐私技术是什么原理？”

*本文原创作者：pingch，本文属FreeBuf原创奖励计划，未经许可禁止转载