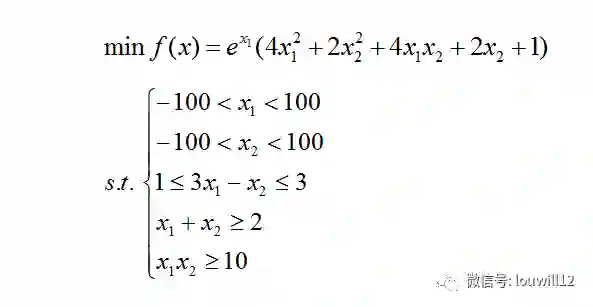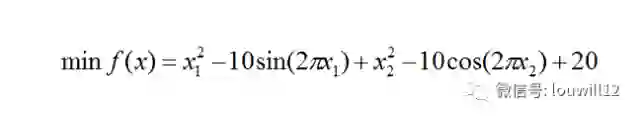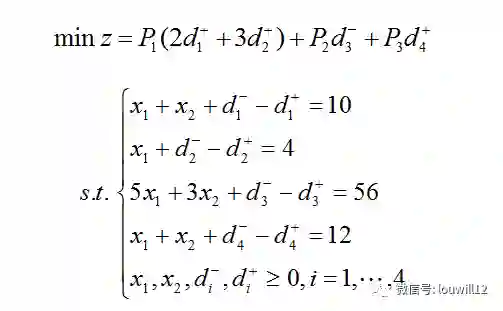R语言与优化模型(一):规划问题和运输问题

作者:鲁伟,热爱数据,坚信数据技术和代码改变世界。R语言和Python的忠实拥趸,为成为一名未来的数据科学家而奋斗终生。
个人公众号:数据科学家养成记 (微信ID:louwill12)
线性规划、整数规划和运输问题
虽说目前数学建模领域大家用的软件工具都是Matlab或者Lingo,但在个人偏好的驱使下还是决定用自己擅长的R语言来实现数学建模算法。就首先从优化模型中简单的线性规划、整数规划以及多目标规划开始。R语言在针对各类优化模型时都能快速方便的求解,对运输问题、生产计划问题、产销问题和旅行商问题等都有专门的R包来解决。

线性规划与整数规划的区别主要在于对决策变量的取值约束有所不同。线性规划的决策变量为正实数,而整数规划则要求决策变量为正整数。在R语言中,有众多相关的R包可以解决这两类问题,例如stat包中的optim、optimize函数,这里给大家推荐Rglpk包,Rglpk包用法简单,核心函数调用方便,对解决大型的线性规划和整数规划问题十分好用。
Rglpk包的核心函数为Rglpk_solve_LP函数,其用法如下:
Rglpk_solve_LP(obj,mat,dir,rhs,types=NULL,max=FALSE,bounds=NULL, verbose=FALSE)
其中obj为目标函数系数,mat为约束矩阵,dir为约束符号,rhs为约束向量,types为变量类型,可选类型有“B”“I”“C”,分别代表0-1变量、正整数和正实数,max为逻辑参数,当其取TRUE 时求目标函数最大值,反之为最小值,bounds为决策变量的额外约束,verbose表示是否输出中间过程的的控制参数,默认为FALSE。
看一个求解线性规划的例子:
library(Rglpk)
obj<-c(10,15,12)#目标函数系数
mat<-matrix(c(5,-5,2,3,6,1,1,15,1),nrow=3)#约束矩阵
dir<-rep("<=",3)#约束符号
rhs<-c(9,15,5)#约束向量
Rglpk_solve_LP(obj,mat,dir,rhs,max=TRUE)#求解
$optimum
[1] 42
$solution
[1] 0.200000 2.666667 0.000000
求解过程清晰明了,比起专业的线性规划软件Lingo有过之而无不及。
再看一例整数规划(0-1规划):
obj<-c(4,3,2)
mat<-matrix(c(2,4,0,-5,1,1,3,3,1),nrow=3)
dir<-c("<=",">=",">=")
rhs<-c(4,3,1)
types<-c("B","B","B")#指定变量类型,模型为0-1规划
Rglpk_solve_LP(obj,mat,dir,rhs,types,max=FALSE)
$optimum
[1] 2
$solution
[1] 0 0 1
整数规划(0-1规划)和线性规划并无本质区别,所以在Rglpk中其实现函数一样,只是依靠types参数来控制两个模型的区别。
运输问题为常见的线性规划问题,但Rglpk包并没有普适性。R针对运输问题、生产计划等问题有专门的R包lpSovle,其核心函数 lp.transport 用法如下:
lp.transport(costs.mat,direction="min",row.signs,row.rhs,
col.signs,col.rhs,presolve=0,compute.sense=0,integers=1:(nc*nr))
其中cost.mat为运费矩阵,direction参数决定取最大值还是最小值,row.sign(产量约束符号)和row.rhs(产量约束向量)构成产量约束条件;col.sign(销量约束符号)和col.rhs(销量约束向量)构成销量约束条件,其余参数可忽略。
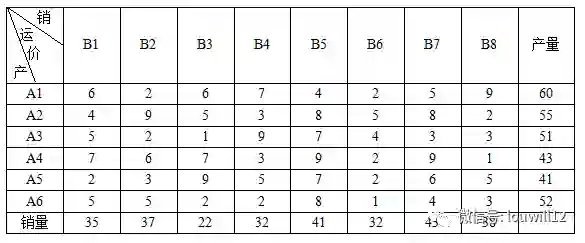
例:使用lpSovle包求解6个生产点和8个销售点的最小费用运输问题。
library(lpSolve)
costs<-matrix(c(6,4,5,7,2,5,2,9,2,6,3,5,6,5,1,7,9,
2,7,3,9,3,5,2,4,8,7,9,7,8,2,5,4,2,2,1,5,8,3,7,6,4,
9,2,3,1,5,3),nrow=6)#运费矩阵
row.signs<-rep("<=",6)#产量约束符号
row.rhs<-c(60,55,51,43,41,52)#产量约束向量
col.signs<-rep("=",8)#销量约束符号
col.rhs<-c(35,37,22,32,41,32,43,38)#销量约束向量
res<-lp.transport(costs,"min",row.signs,row.rhs,col.signs,
col.rhs)
res
Success: the objective function is 664
res$solution
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 0 19 0 0 41 0 0 0
[2,] 0 0 0 32 0 0 0 1
[3,] 0 12 0 0 0 0 39 0
[4,] 0 0 0 0 0 6 0 37
[5,] 35 6 0 0 0 0 0 0
[6,] 0 0 22 0 0 26 4 0
由R输出结果可知6个生产点8个销售点的最小运费为664,相应的运送方案为A1→B2:19个单位,A1→B5:41个单位,A2→B4:32个单位,A2→B8:1个单位,A3→B2:12个单位,A3→B7:39个单位,A4→B8:37个单位,A5→B1:35个单位,A5→B2:6个单位,A6→B3:22单位,A6→B6:26个单位,A6→B7:4个单位。
非线性规划与多目标规划
与线性规划不同的是,非线性规划要求目标函数或约束条件中含有非线性函数。相应的求解这类问题就要用到非线性规划的方法。约束条件或者目标函数的放宽使得规划模型更具普适性,但也增加了问题求解的难度。对于简单的非线性规划问题,R语言中stat包即可求解。在这里我们给大家介绍R语言中求解非线性规划更为专业的Rdonlp2包。

Rdonlp2在求解非线性规划问题上功能十分强大,用户可自行安装并查阅帮助文档:
library(Rdonlp2)
Rdonlp2包的核心函数为 donlp2,可以快速求解非线性规划的最值。其用法如下:
donlp2(par,fn,
par.upper=rep(+Inf,length(par)),
par.lower=rep(+Inf,length(par)),
A=NULL,
lin.upper=rep(+Inf,length(par)),
lin.lower=rep(-Inf,length(par)),
nlin=list(),
nlin.upper=rep(+Inf,length(nlin)),
nlin.lower=rep(-Inf,length(nlin)),
control=donlp2.control(),
control.fun=function(lst){return(TRUE)},
env=.GlobalEnv,
name="Rdonlp2"
)
对该函数众多参数进行解释:
par : 初始迭代向量
fn : 连续型函数
par.upper、par.lower : 自变量的上下限
A:线性约束矩阵
lin.upper、lin.lower : 线性约束条件的上下界
nlin : 非线性约束条件函数列表
nlin.upper、nlin.lower : 非线性约束条件的上下界
其余参数可忽略。
先看一例donlp2函数求解非线性规划的例子:
用Rdonlp2包编写非线性规划计算命令:
library(Rdonlp2)
p=c(0,0) #迭代初始值
par.l=c(-100,100);par.u=c(100,100)#自变量定义域约束
fn=function(x){
exp(x[1])*(4*x[1]^2+2*x[2]^2+4*x[1]*x[2]+2*x[2]+1)
} #目标函数
A=matrix(c(1,1,3,-1),2,byrow=TRUE)
lin.l=c(2,1);lin.u=c(+Inf,3) #线性约束
nlcon1=function(x){
-x[1]*x[2]
} #非线性约束
donlp2(p,fn,par.u,par.l,A,lin.l=lin.l,lin.u=lin.u,
nlin=list(nlcon1))
$message
[1] "KT-conditions satisfied, no further correction computed"
$par
[1] 33.66667 100.00000
$gradf
[1] 1.625065e+19 2.243635e+17
相应运行结果包括中间过程、算法参数、运行时间等数据,这里就不全部列出。
再看一例利用Rdonlp2包求解二元rastrigin函数最小值的问题。该函数因为有众多极值点而仅有一个最值点对各类优化算法有一定的欺骗性,但用其来测试各类优化算法效果显著。该二元rastrigin函数为:
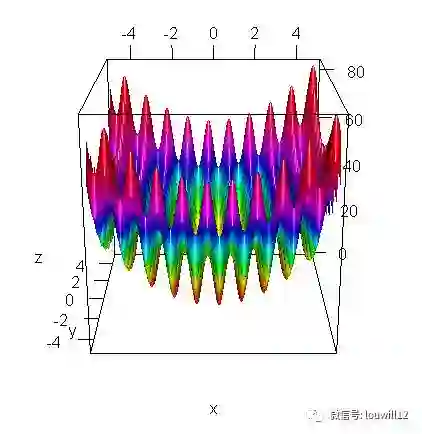
先作出该函数的三维图像:
a<-5
x<-seq(-a,a,0.01)
y<-seq(-a,a,0.01)
f<-function(x,y){
x^2-10*sin(2*pi*x)+y^2-10*cos(2*pi*y)+20
}
z<-outer(x,y,f)
image(x,y,z,col=heat.colors(24))
library(rgl)
zorder<-rank(z)
persp3d(x,y,z,col=rainbow(as.integer(max(zorder)))[zorder])
fn<-function(x){
f<-sum(x^2*cos(2*pi*x)+10)
}
par<-c(-500,500)
ret<-donlp2(par,fn)
ret$f
[1] 20
ret$par
[1] -2.654965e-06 2.654965e-06
由输出结果可知该函数最小值为20 。所以Rdonlp2求解非线性规划也是非常方便的。当然了,还有很多更为一般的非线性规划问题是Rdonlp2包也不能解决的,这时候可能会向遗传算法、模拟退火这些启发式算法求助啦。这里且不作讨论。
在许多实际问题中,衡量一个方案的好坏标准往往不止一个,例如制造一枚导弹,既要射程远又要最省燃料,还得精度高。这一类问题就不是单一的目标规划问题了,我们称之为多目标规划问题。
求解多目标规划问题通常有主要目标法、分层序列法和线性加权求和法等方法。其中主要目标法通过确定一个主要目标,将多目标优化问题转化为线性或非线性规划问题;分层序列法是将目标中多个目标按照其重要程度排一个次序而逐步求解的过程;线性加权法则是对各目标赋予一个权数,加权求和得到一个新的目标函数而进行求解的过程。
R语言中多目标规划问题的求解通常用goalprog包,其核心函数为llgp:
llgp(coefficient,targets,achievements,maxiter=1000,verbose=FALSE)
其中coefficient为约束系数矩阵,targets为系数矩阵约束向量,achievements是包含objective、priority、p、n的目标函数,其中objective表示第几对偏差变量,priority表示该偏差变量的优先级,p和n分别为正负偏差变量的权系数。
看一道多目标规划问题计算实例:(该题来自钱颂迪《运筹学》教材4.4节例5)
llgp函数计算过程如下:
library(goalprog)
coefficients<-matrix(c(1,1,5,1,1,0,3,1),4)
targets<-c(10,4,56,12)
achievements<-data.frame(objective=1:4,priority=c(1,1,3,4),
p=c(2,3,0,1),n=c(0,0,1,0))
soln<-llgp(coefficients,targets,achievements)
soln$converged
[1] TRUE
soln$out
Decision variables
X
X1 4.000000e+00
X2 6.000000e+00
Summary of objectives
Objective Over Under Target
G1 1.000000e+01 0.000000e+00 0.000000e+00 1.000000e+01
G2 4.000000e+00 0.000000e+00 0.000000e+00 4.000000e+00
G3 3.800000e+01 0.000000e+00 1.800000e+01 5.600000e+01
G4 1.000000e+01 0.000000e+00 2.000000e+00 1.200000e+01
Achievement function
A
P1 0.000000e+00
P2 0.000000e+00
P3 1.800000e+01
P4 0.000000e+00
由输出的结果我们可以看到x1、x2最优值分别为4和6。
由该例我们可以看出,R语言求解多目标规划问题只需按照函数格式将规划的目标函数、约束条件套入格式即可,过程非常简单。
参考文献:
魏太云.R软件与最优化[C]//中国r语言会议.2008.
公众号后台回复关键字即可学习
回复 爬虫 爬虫三大案例实战
回复 Python 1小时破冰入门回复 数据挖掘 R语言入门及数据挖掘
回复 人工智能 三个月入门人工智能
回复 数据分析师 数据分析师成长之路
回复 机器学习 机器学习的商业应用
回复 数据科学 数据科学实战
回复 常用算法 常用数据挖掘算法