斯坦福提出机器学习开发新思路：无Bug的随机计算图Certigrad（已开源）

2017 年 7 月 12 日 机器之心

选自Github

机器之心编译

参与：李泽南、蒋思源

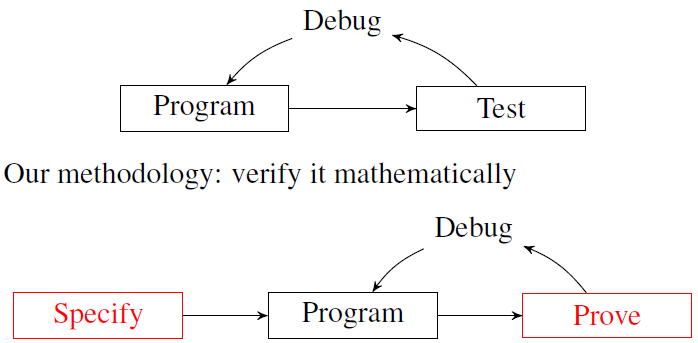
在实践中，机器学习算法经常会出现各种错误，而造成错误的原因也经常难以找到。近日，斯坦福大学的研究者提出了一种开发机器学习系统的新思路：以数学定理为基础构建机器学习随机计算图，以达到无 bug、自动化的目的，他们提出了随机计算图系统 Certigrad。在实验中，研究人员证明了该方法在未经大量优化的情况下达到了可以和 TensorFlow 相媲美的表现。目前，该项目已经开源。

项目链接：https://github.com/dselsam/certigrad

Certigrad

Certigrad 是一个概念证明，它是一种开发机器学习系统的新方法，其中包含以下组件：

应用本身
基础数学库
应用在数学上所需求的形式化描述
应用满足其形式化描述的机器可测证明

具体地说，Certigrad 是一个优化随机计算图的系统，研究人员使用 Lean Theorem Prover 对其进行了系统性的除错，它最终在底层数学上被证明是正确的。

背景：随机计算图

随机计算图通过允许节点代表随机变量，和定义损失函数为叶子结点在全图中随机选择的预测值之和，扩展了 TensorFlow 和 Theano 这些系统的计算图。Certigrad 允许用户从该项目提供的基元中构建随机计算图。创造这一系统的主要目的是找到一个能够描述随机计算图，并运行随机算法（随机反向传播）的程序。同时期望对参数损失函数梯度进行采样。

正确性

随机反向传播

以下定理可以证明我们的随机反向传播实现是正确的：https://github.com/dselsam/certigrad/blob/master/src/certigrad/backprop_correct.lean#L13-L25

通俗地说，它表示：对于任何随机计算图，backprop 计算了张量的向量，如此，每一个向量元素都是一个随机变量，这个随机变量等同于关于此参数的图的期望损失梯度。

更通俗地说：∇ E[loss(graph)] = E[backprop(graph)]

优化验证

研究人员实现了两个随机计算图转换，一个是对图进行「重新参数化」（reparameterize），让随机变量不再直接依赖于一个参数；另一个用于整合多元各向同性高斯（multivariate isotropic Gaussian）的 KL 散度。

https://github.com/dselsam/certigrad/blob/master/src/certigrad/kl.lean#L79-L90
https://github.com/dselsam/certigrad/blob/master/src/certigrad/reparam.lean#L70-L79

验证 Certigrad 程序属性

Certigrad 还包括构建随机计算图的前端语法。这里是一个解释原生变分自编码器的示例程序：

https://github.com/dselsam/certigrad/blob/master/src/certigrad/aevb/prog.lean#L16-L38

研究人员证明了上述两个经过验证的优化的确符合原始自动编码器的顺序：

https://github.com/dselsam/certigrad/blob/master/src/certigrad/aevb/transformations.lean#L52-L57

反向传播在结果模型上已被证明可以正确运行，它可以满足所有必要前提条件：

https://github.com/dselsam/certigrad/blob/master/src/certigrad/aevb/grads_correct.lean#L20-L27

正式证明

在证明定理的过程中，Lean 构建了一个正式的证书，它可以通过一个小型独立可执行程序进行自动验证，它的可靠性是基于构建良好的元理论嵌入到 Lean 的逻辑核心中，而 Lean 的可靠性已被大量开发者所证明。

问题

尽管在证明期间研究者们使用了非常高的标准，但 Certigrad 仍然有一些不够理想的地方。

我们对其数学基础进行了公理化，而不是从基本原理的层面上进行构建。
在一些地方我们采用了浮点数，即使我们的正确性定理只适用于无限精度的实数。
为了保证性能，我们在运行时用 Eigen 调用替换原始张量运算。
系统在虚拟机中执行，该虚拟机的设计不像核心逻辑的证明检验程序那样值得信赖。

表现

能被证实的正确性原则就不需要再牺牲计算效率了：证明只需被检查一次，而且不会带来过多的运行成本和运行时间。尽管目前经过我们验证的算法缺乏很多优化措施，机器学习系统的大多数训练时间都花费在了乘法矩阵上，我们仍能够通过与矩阵运算的优化库（Eigen）进行链接来轻松达到具有竞争力的表现水平。我们在 MNIST 上使用 ADAM 训练了一个自编码变贝叶斯（AEVB）模型，发现该模型的表现和 TensorFlow 相比具有竞争力（在 CPU 上）。

使用 ADAM 在 MNIST 上训练 AEVB 的脚本：https://github.com/dselsam/certigrad/blob/master/src/certigrad/aevb/mnist.lean#L44-L66

优势

尽管新方法面临一些挑战，但它的优势是显而易见的。

调试

首先，新方法提供了一种系统性的调试机器学习系统的方法。

执行错误（Implementation errors）在机器学习系统中非常难于探测——更不用说本地化和问题解决——而且还有其他潜在的不良影响。例如；一个执行错误可能会导致不正确的梯度，让整个机器学习算法停顿，但这种情况也可能是由于训练的数据中存在噪音、错误设置、优化不合适、搜索策略不对或数值不稳定而引起的。这些其他问题是如此之常见，以至于我们通常认为任何不良行为都是由其中的一部分引起的。

因此，在实现中出现的错误如果没有被检测到，将会无限期地存在下去。而在随机系统中，错误更加难以检测，因为一些错误可能会扭曲随机变量的分布，可能需要编写定制的统计测试才能被检测出。

通过我们的方法，正式规范可以用来在逻辑层面上对机器学习系统进行彻底的测试与调试，完全不需要进行经验主义的测试。而证明规范的过程将揭示所有实现错误，疏忽和隐含假设。一旦得到证实，每个利益相关方都可以确定实现是正确的，而无需依赖于任何有关人员，或去了解程序是如何运行的。

合成

第二，我们的方法可以让一些实现的工作半自动地完成。

而使用现在的方法，编译器完全无法知晓自己需要做什么——它们只能捕捉语法错误，而新方法可以用定理推出程序需要做什么，并提供更多有意义的帮助。举一个简单的例子，假设我们需要将双层 MLP 编译成一个单原始运行器，避免图处理时需要消耗的计算资源。通常这需要包括手工打造的梯度函数。但在新方法中，定理证明器知道如何使用数学方法，包括相关的梯度规则和张量的代数性质，它可以帮助推导出新算子的梯度。

合成的可能性不仅仅是简单的自动化代数推导。在开发 Certigrad 时，研究人员证明了系统中所有复杂部位的可实现性，并使用这一过程所产生的证明义务来帮助确定程序需要做什么。正式规范最终是机器可检验的正确性证明，它使得我们能够正确地实现系统，而无需对「为什么系统正确」采取一致的全局理解。同样，大多数这样的负担被留给了电脑。

侵略性最优化（Aggressive optimizations）

第三，我们的方法可以使得稳定自动化更主动地进行转换。例如，我们可以编写一个程序来搜索随机计算图的构建元素，这样就能用分析方法进行整合，因此可以充分利用积分恒等式的大型库，和很难由手动进行模拟的程序方法。这样的过程可能在许多模型上实现超人为方差缩减，但可靠的实现会极其困难。如果该过程能为给定转换生成机器可测的数字证书，那么转换是可信的，且无需考虑过程本身的复杂性。

文档

第四，形式规范（即使没有正式的证明）也可以作为系统的精确文档，它同样可以让我们理解代码的各部分到底是在做什么、各个部分假设了什么样的先决条件和保持了怎样的不变量。这种精确的文档对于任何软件系统都是很有用的，但对于机器学习来说格外的有效，因为并不是所有的开发者都有必要的数据专业基础来填补非正式描述的鸿沟。

递增

对于高安全等级（high-assurance）系统，我们的系统已经十分节约计算资源了，但仍然需要很多的研究工作才能使其适应主流发展，因为正确性只是一个」选项「。然而，我们方法的一个关键方面可以递增地接受。我们只能在 Lean 中写一点代码，并简单的对其它部分进行打包和公理化（如同我们在 Eigen 所做的一样）。我们也可以写下来浅层的正确性属性，并只证明其中一小部分属性。我们希望随着时间的推移和工具的发展，开发者能发现进一步应用我们的方法是非常值得的。

搭建 Certigrad

Lean 还处于开发阶段，我们也更进一步地努力使得 Certigrad 可以简单地进行安装。与安装 Certigrad 特别相关的是外部功能接口（FFI）。我们复制了 Lean 项目以添加代码将 Eigen 打包入 Lean 虚拟机中，但是很快 Lean 将有一个外部功能接口，我们也就不需要重新构建 Lean 而添加到虚拟机中了。一旦 FFI 发布了，我们将把 Certigrad 移动到 Lean 的主分支下。

在那之前：

下载我们复制的 Lean（地址：https://github.com/dselsam/lean/tree/certigrad），并且按照指导手册进行构建/安装（地址：https://github.com/leanprover/lean）。
下载 Eigen 并安装它（http://bitbucket.org/eigen/eigen/get/3.3.4.tar.bz2）。
下载该仓库（Github 中的当前 repository），并在主目录下执行 leanpkg—build。

注意：构建 Certigrad 一般会话 15 分钟左右，并至少需要 7GB 的内存。

注意

我们已经在形式上证明了 Certigrad 是正确的（如上文所述对误差取模），但是这并不意味着 Certigrad 就会那样实现。所有这些都意味着给定假设下上述的定理都是正确的。Certigrad 是为概念证明而设计的，它不是一个产生式系统。而要令其如同工具那样有用，我们还需要添加大量的特征。在开发过程中，为了使方法更加经济，我们遇到了许多需要解决的问题。我们更关心如何解决这些挑战，而不是扩展和维护 Certigrad 本身。

更多信息

斯坦福大学的研究人员发表了一篇论文描述了 Certigrad 背后的想法，该论文已被 ICML 2017 大会接收，下面机器之心将简要介绍该论文。

论文：Developing Bug-Free Machine Learning Systems With Formal Mathematics

论文链接：https://arxiv.org/abs/1706.08605

数据噪声、非凸目标函数、模型参数误设和数值不稳定都将导致机器学习系统出现达不到期望的行为。因此，检测实际实现中的误差是极其困难的。我们展示了一种方法，开发者可以使用一个交互式验证助手来实现他们的系统，并且证明和定义他们系统正确性的正式定理。在验证助手中，交互地证明定理会揭示所有实现误差，因为程序的任何误差都会导致最后证明的失败。作为案例研究，我们实现了一个新系统 Certigrad，它可以优化随机计算图，并且我们可以得到一个真实的证明（机器可检测），即系统抽样的梯度是真实数学梯度的无偏估计。我们使用 Certigrad 训练了一个变分自编码器，并发现其性能和在 TensorFlow 中训练相同模型的情况相差无几。