WWW'22| 码率衰减的几何图表示学习

2022 年 5 月 6 日 图与推荐

论文地址：https://arxiv.org/pdf/2202.06241.pdf
论文ppt地址：https://ahxt.github.io/files/WWW2022_slides.pdf
欢迎关注小编知乎：戴鸽

这篇文章总体而言是一个无监督的学习策略。在图表征学习中引入码率衰减的概念，使得图表征两两正交，达到不同类别的节点有较强区分度，且同类型节点又能内部更紧凑。

简介

图节点表征的学习方法总体来说可以分为基于随机游走和基于对比学习的方法，但是现有方法，如DeepWalk或者GRACE，都是针对局部节点的，忽略了节点的全局信息。因此，这篇文章主要解决的问题就是如何合理利用全局信息来改善节点表征，使其学习时能考虑图的整体结构。然而，这个问题仍然是有难点的，如果用简单的聚类方法去聚合这些多样化的信息，则又会导致引入额外的噪音信息。因此，作者引入最大化码率衰减的方式来学习节点表征的方法来学习图的几何特征，即Geometric Graph Representation Learning ( )。模型整体流程如图所示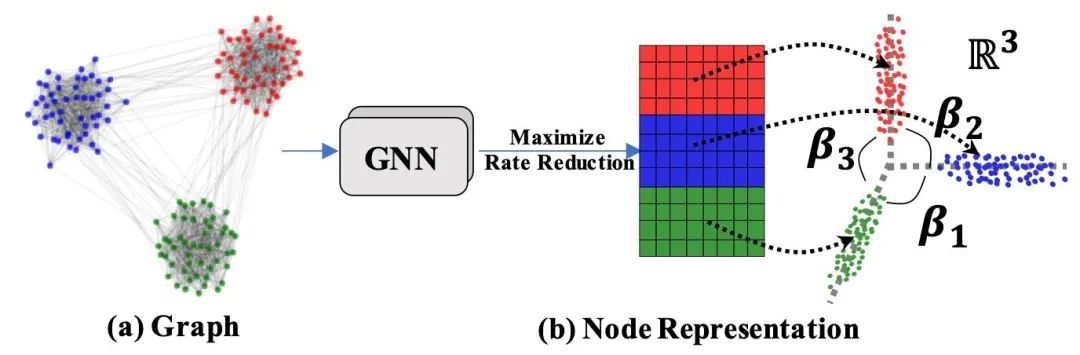：首先使用最大化码率衰减将不同组群的节点映射到不同的子空间上，然后优化这个子空间里面的信息，使得每个子空间紧致，而不同子空间分散。

方法

将图定义为，节点特征为，编码转化以后为，邻接矩阵为，这里的邻接矩阵定义的有些特别，是用一组一组的向量对每个节点的邻居进行表示，主要是要衔接后面在码率上的表述。

接下来可以开始介绍最大化码率衰减是什么了。这是一种来自于信息论的东西，用来衡量数据上的紧凑性。如果码率越低，那么意味着信息越紧凑，而码率衰减高，则表示不仅同组的信息紧凑，而且不同组的信息能够尽可能区分。首先，为了保证全局信息的多样性，即不同组的信息可以很好的分开，那么就意味着这里的码率需要更大：

表示为单位矩阵，为容错率。接下来加入子空间元素，衡量同组信息是否紧凑，由于假设了一个节点可能来自于不同的子空间，所以可以用概率矩阵

将节点特征映射到个子空间。并且，。由此可以构建针对子空间的概率矩阵

，将这个子空间映射信息加入码率以后就能转换成：

对于衰减量，则是结合前文所述，既需要尽可能覆盖所有数据使其分离成不同组，又能保证每个子空间能内部紧凑，因此定义为：

对于图来说，码率可以依附于边的传播。如果考虑单个子空间，对于每一个节点的边向量，这一组节点群的矩阵可以写成，码率可以写成：

对全局所有节点，则有矩阵集合，每一组节点码率则表示为：

其中表示节点平均度数。之后，将得到的两种码率表示方法带入码率衰减量的表示，并且在额外加入两个超参和进行微调：

在训练时希望这个值越大越好，而实际上训练的时候只会考虑编码部分的参数训练，即怎么得到的数值。

一点理论分析

其实最关心的还是说凭什么这个方法就能保证节点之间的全局差异性能够被区分开来，所以将注意力放在上。这个式子可以分解为：

这里。如果两个子空间正交，那么他们的cos值应当趋近0，sin则会趋近1。而如果优化目标是使得这一项尽可能大，那么理所应当可以使得这里的子空间尽可能分离。另外这个优化的第二项不会影响到这里的，详情可以参考原文。

实验

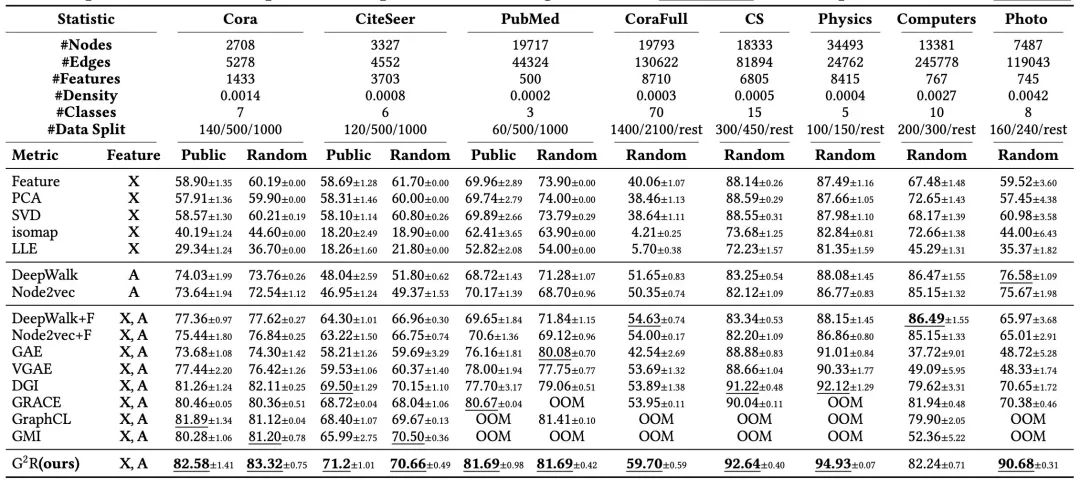
将无监督的表征结果单独拿出来以后用逻辑回归分类器做简单判别，可以得到以下结果。从实验效果来看的表征更能学到有区分度的表征。将得到的表征用PCA降维以后可以观测不同类别之间是否真的两两正交：这里每一个小图只有两个类别，可以很明显的发现两组节点信息真的可以有明显的区分度，而群组内部的信息也很容易聚合在一起。