机器学习PAI实战：玩转人工智能之你最喜欢哪个男生？

2019 年 3 月 26 日 云栖社区

前言

分类问题是生活中最常遇到的问题之一。普通人在做出选择之前，可能会犹豫不决，但对机器而言，则是唯一必选的问题。我们可以通过算法生成模型去帮助我们快速的做出选择，而且保证误差最小。充足的样本，合适的算法可以透过表象的类别，进而挖掘其内在的联系、区别，找出最佳的的属性来区分每个样本的类别。所以说学习和应用机器学习的算法，要求我们必须非常了解数据实例，每个样本数据有多少个特征，哪些特征是敏感的，特征分布如何。只有充分了解数据，才能选择最合适的算法。

场景描述

单身王女士经常逛某相亲网站，前前后后浏览了1000个男生，并给他们打标了，不喜欢、一般喜欢、很喜欢三个类别。该相亲网站的工程师，决定开发一个算法推荐模型，给王女士依次推荐很喜欢，一般喜欢的男生。并可以将这个算法模型应用到网站，吸引更多的单身青年注册使用，并可以找到自己喜欢的男/女朋友。

数据分析

首先将离线数据导入到odps表中。我们主要介绍使用散点图和箱线图来直观的观测分析数据。然后根据上面的具体案例来学会如何看，理解这个图形。数据选自《机器学习实战》一书。

散点图

详情

https://help.aliyun.com/document_detail/42716.html

拖拽统计分析-散点图。如图所示，选择观测的特征。

右键查看分析报告

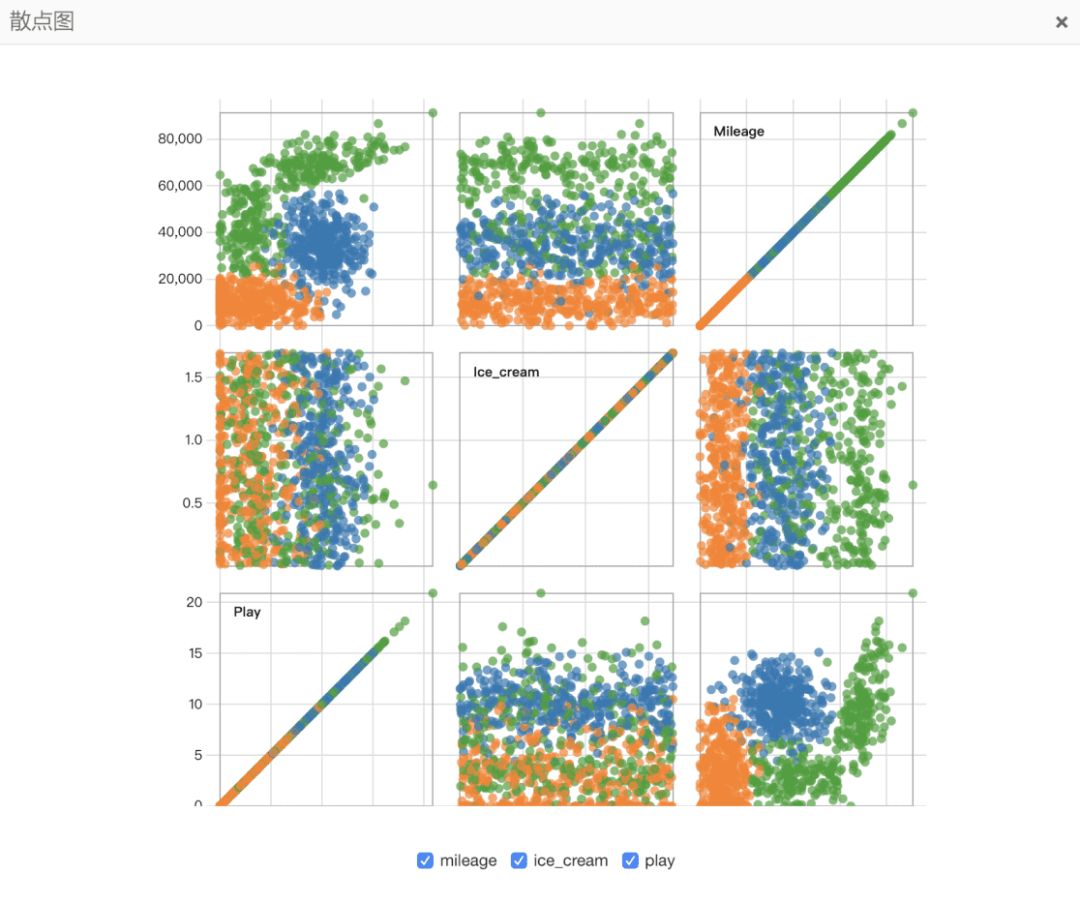
散点图介绍

1，反对角线上的三个方形，在方形左上角表明三个特征的名称。而且这个三个图像与其他图形不相同，横纵坐标都是一个特征，则对角直线就代表该特征在不同类别下分布密度。比如Play这个方形，我们发现黄色部分集中在下方，蓝色部分主要分布在中间，绿色主要分布在中上方。

2，除了反对角线上的三个方形，其他方形则是反映了两两特征之间的分布情况。比如第一排第一列（1，1），横坐标为play，纵坐标为mileage。从这个方形上可以直观观测出不同颜色的散点集中分布在不同区域。

3，关于反对角线对称的两个方形，则是两个特征交换纵横坐标的散点图。

4，在整个散点图的下方，可以勾选你希望对比的特征。

通过上面散点图，我们可以比较清晰得出几个结论。

1，ice_cream特征对分类不敏感。从图（1，2），（2，2）我们可以直观看出，ice_cream在所有类别中几乎都是均匀分布。

2，mileage，play 特征可以将类别明显的划分成三个区域。说明这两个特征绝大程度上决定了类别的划分。

散点图进阶使用

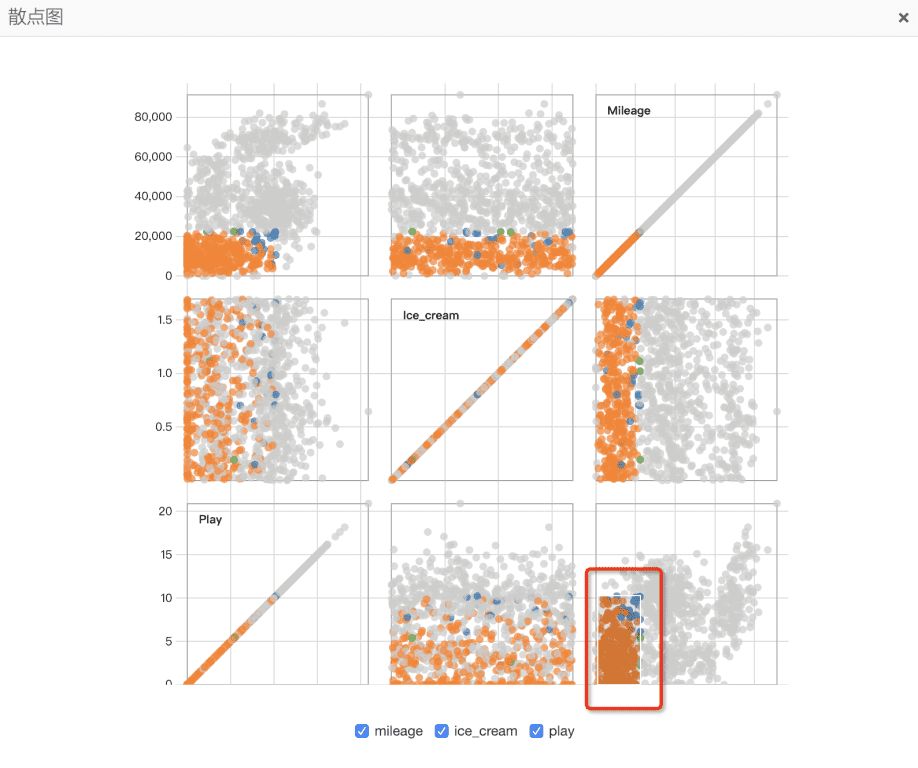
在任意个方形内，拖拽一个方形区域，可以选出满足这些特征的样本，更加直观的观测，这些样本在不同方形内的分布。如上图所示，我们选中了图（3，3）内一个方形区域，可以看出这些样本在ice_cream特征下是均匀分布，在其他两个特征下，都可以通过一个超平面划分。

箱线图

详情

https://help.aliyun.com/document_detail/42716.html

拖拽统计分析-箱线图。如图所示，选择观测的特征。

箱线图介绍

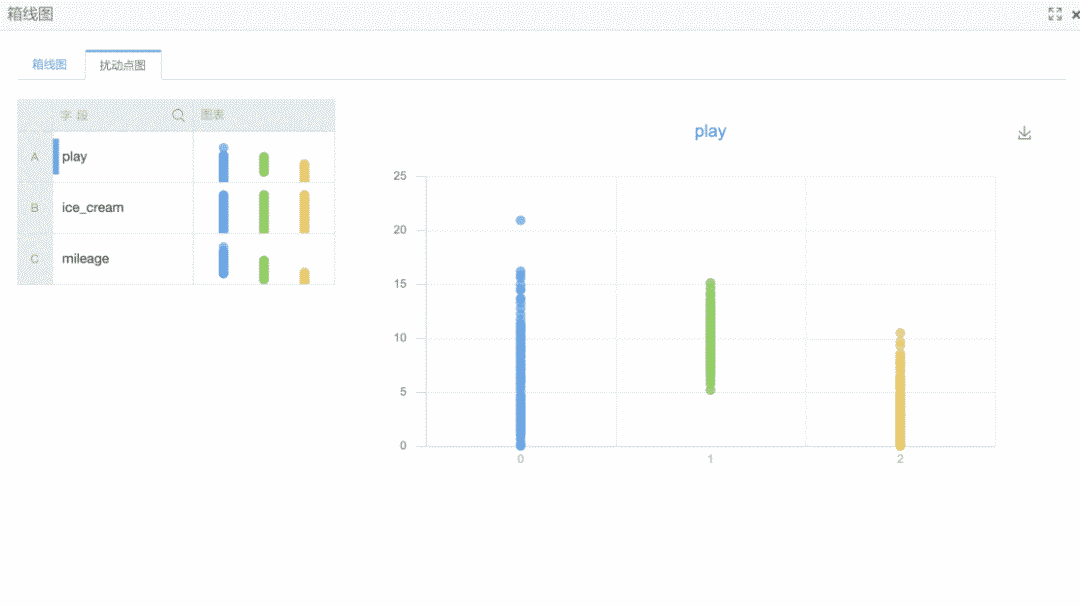
1，箱线图组件分两个tab分别显示箱线图和扰动点图，在左上角都可以选择观测不同的特征。右侧显示该特征下，每个类别的分布情况。

2，箱线图介绍，每个类别的箱线图，从上到下一共有5条横线。

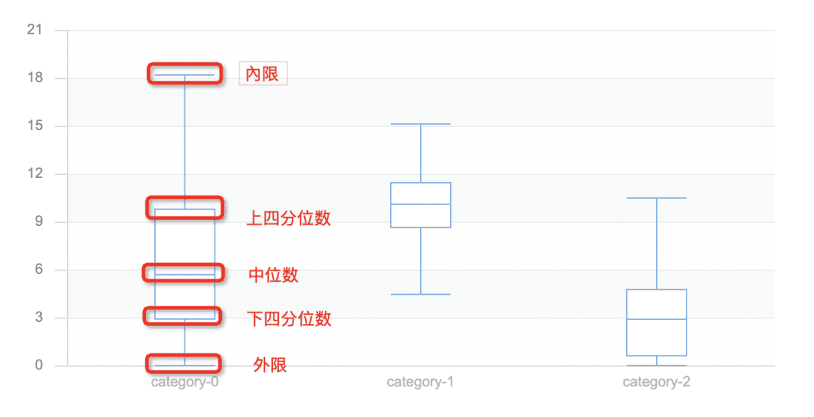
3，內限不是样本的最上限，外限也是不最下限，超过內限和外限的样本为异常样本。

4，结合扰动点图，我们可以发现观测到异常样本的大致数量多少。

箱线图分析

1，通过上面的图，我们可以关注paly属性在不同类别下的分布。对比ice_cream特征

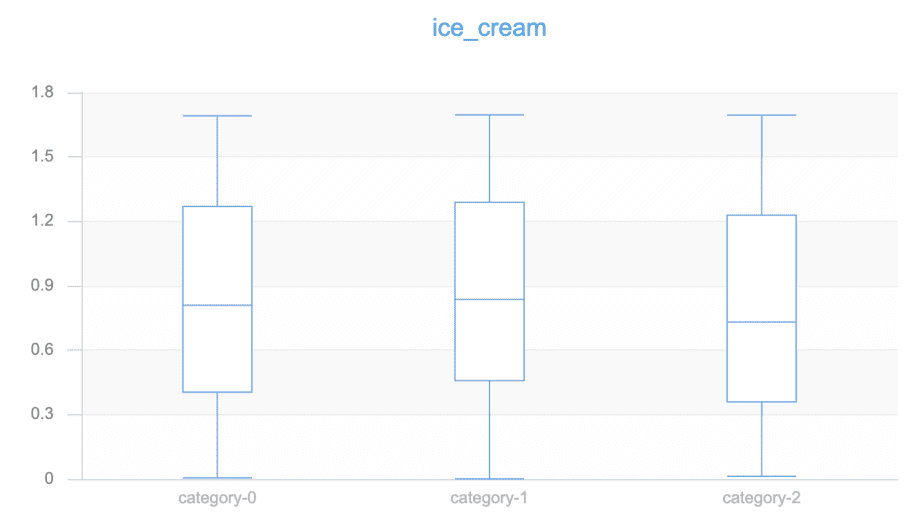
我们发现paly特征的属性值在不同类别下有明显有倾向性分布。而ice_cream在不同类别下分布几乎是一样的，这也验证了我们通过散点图得出的结论。

场景抽象化

现在回到我们一开始遇到的问题。如何用算法帮助工程师为王女士推荐其他她可以喜欢的男生呢。其实这是一个简单的问题，就是把所有的男生分为三类，不喜欢，一般喜欢，很喜欢。对于一个没有标签的男生(x)，我们分出其最可能属于哪个类别的概率(p)。

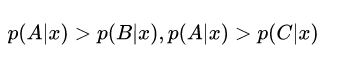
在这种情况下，我们就选出这个男生属于类别A。如何计算这个概率，不同算法有不同的计算方法。比如K紧邻算法，选出离这个样本点最近的K个样本，通过属于A的样本个数除以K就可以得出属于A的概率。随机森林，则是通过投票的方式，票数多的类别就是样本最终划分的类别。

模型选择

通过前面数据分析，我们知道了数据的一些特性。

1，mileage数值比其他两个特征大很多，在计算特征间的距离时，所在权重就比较大。所有选择K近邻可以会造成较大误差。

2，AdaBoost算法，随机森林以及逻辑回归算法都可以处理数值型数据，所以这三种算法我们都会尝试，并评估者三个算法的准确率。

数据处理

我们可以使用统计分析-全表统计观测数据是否有空值，以及一些方差等的统计信息。在本案例中我仅做缺失值检测。

模型训练

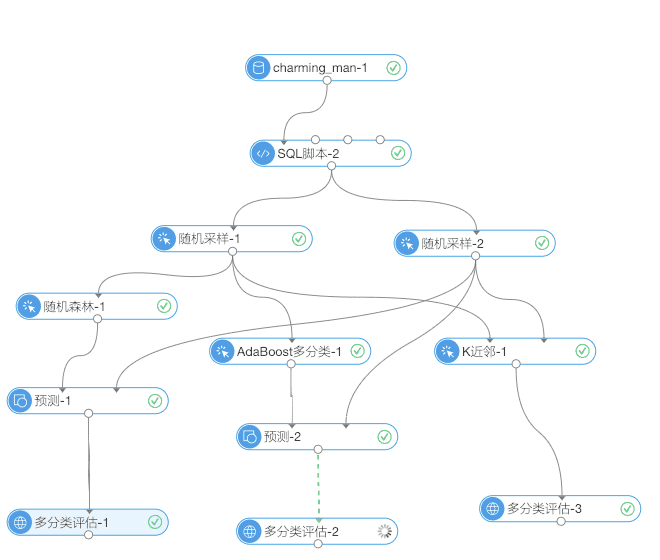
我们分别选择了三个分类算法，随机森林、AdaBoost、K近邻算法。分别做了训练，预测和算法评估。在下面我们会通过测试评估来选择合适的方案。

模型测试

随机森林算法

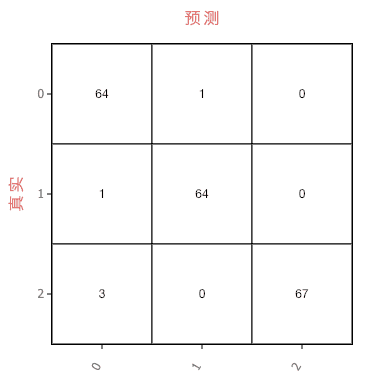
AdaBoost算法

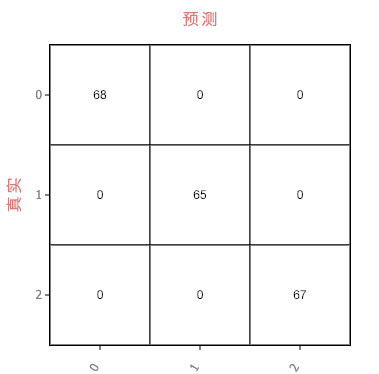
K近邻算法

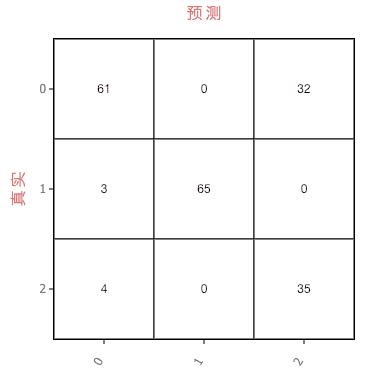
通过上面的混淆矩阵，可以很直观的看出，在算法准确度层面，AdaBoost>随机森林>K近邻。也验证了我们前面通过数据分析得出的结论，在某个特征的值过大时，K近邻算法容易出现较大的误差。当然我们可以通过归一化来处理这些特征值，只是这样做在服务测试时，输入的数据就必须是归一化的值而不是真实数据，在实际使用中会有一些麻烦。

模型部署和测试

模型的部署和测试参见【玩转人工智能—基于PAI的机器学习实战系列二】商品价格预测

https://yq.aliyun.com/articles/692330

总结

AdaBoost之所以有如此好的效果，其功劳要归功于集成算法的提出和应用。集成算法通过组合多个分类器的结果，并赋予不同的权重值，而获得了比任一个分类器都要好的结果。当然这也做也有一定风险，比如说有可能加深了分类器的过拟合问题。

在分类问题上，我们最常遇到的问题就样本分布不均衡的问题。就是说正样本多与负样本，某个类别的样本多与其他类别的样本。这样的数据集在大部分分类器上都会存在问题，通常情况下，我们可以通过欠抽样或者过抽样来解决这类问题，但是在实际操作中，我们需要注意下，如何才能在尽可能不影响实际真实性的情况下做到很好的抽样。

人人用得起的机器学习平台↓↓↓↓