[算法与数据结构] 《算法导论》堆排序笔记

[点击蓝字，一键关注~]

堆排序的实现是靠叫做“堆”的数据结构来实现的。所以学习堆排序，首先要了解什么是堆

堆

堆是一个数组，每个结点表示数组中的一个元素，堆可以看做是一个近似的完全二叉树。完全二叉树是所有叶结点深度相同，且所有内部结点度为2的2叉树。

树的高度：从结点x向下到某个叶结点最长简单路径中边的条数

表示堆的数组A包括两个属性：A.length给出数组元素的个数，A.heap-size表示有多少个堆元素存储在该数组中。

最大堆和最小堆

最大堆：除了根以外的所有结点i都要满足

A[PARENT(i)] >= A[i]

意思是，某个结点的值至多与其父结点一样大。因此，堆中的最大元素存放在根结点中；并且在任一字树中，该字树所包含的所有结点的值都不大于该字树根结点的值。

最小堆： 除了根以外的所有结点i都有

A[PARENT(i)] <=A[i] 

最小堆中的最小元素存放在根结点中。

在堆排序中，一般使用最大堆，最小堆用于构造优先队列。

高度：堆中结点的高度为该结点到叶结点最长简单路径上边的数目。

MAX-HEAPIFY过程：

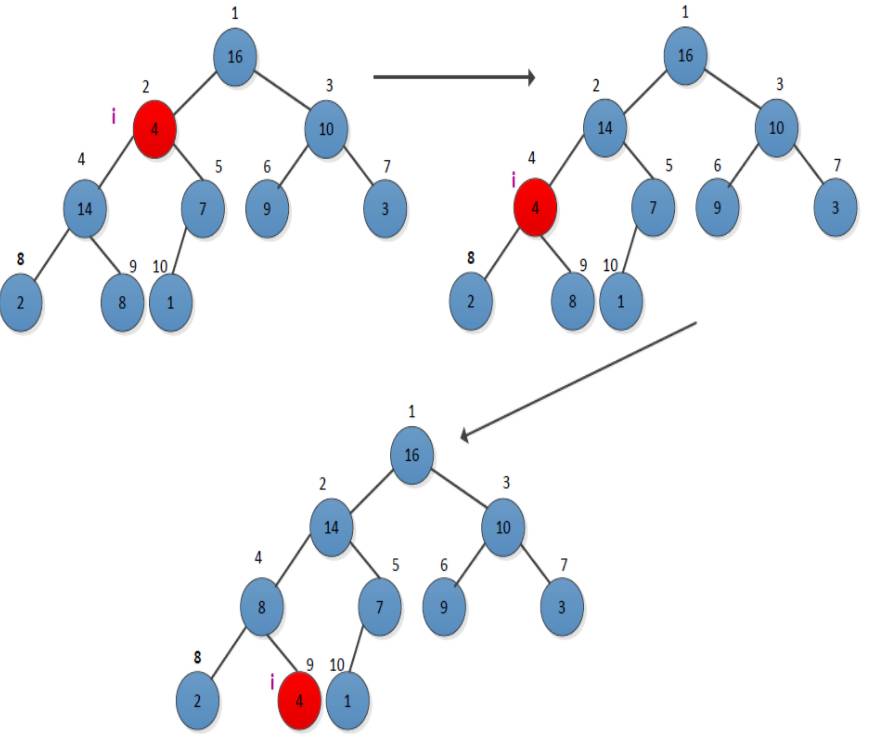
这个过程的意思其实很简单，就是如果所建的堆不满足堆的性质的时候，如何来调整的过程。下图是书中的栗子，当i=2的时候，就是第二个元素，4小于其叶子结点14，应该调整为他右边的样子，交换4和14的位置，然后交换以后发现4和8又不满足堆的性质了，所以递归上面这个过程，这时候i=4。得到下面那个图，此时不再有数据交换发生。时间负责度为O（h），h为树的高度。

建堆

建堆的意思怎么把一个数组转换为一个最大堆。算法伪代码如下：

BUILD-MAX-HEAP(A)

A.heap-size = A.length

for i =[A.length/2] downto 1

        MAX-HEAPIFY(A,i)

算法的时间复杂度是O（n）。

堆排序

初始时候，堆排序算法利用建最大堆的过程BUILD-MAX-HEAP将输入数组A[1..n]建成最大堆，n=A.length。因为数组中最大元素总在根结点A[1]中，如果不在根结点，则通过把它与A[n]进行交换，将最大元素放到根结点，然后去掉根结点，这时候原来根结点的孩子结点仍然是最大堆，而新的根结点可能会违背最大堆的性质，如果不满足，则继续调用MAX-HEAPIFY（A,i），从而在A[1..n-1]上构造新的最大堆，堆排序就是一直重复这个过程，直到堆的大小从n-1降到2.

算法伪代码如下：
HEAPSORT（A)

BUILD-MAX-HEAP（A）

for i = A.length downto 2

        exchange A[1] with A[i]

        A.heap-size = A.heap-size -1

        MAX-HEAPIFY(A,1)

最后写一个堆排序的Python实现

# 最大堆建立过程
def sink(Ary, k, end_num):
    while 2 * k < end_num:
        j = 2 * k
        if Ary[j] < Ary[j + 1]:
            j += 1
        if Ary[k] > Ary[j]:
            break
        Ary[k], Ary[j] = Ary[j], Ary[k]
        k = j

# 堆排序
def heap_sort(Ary):
    end_num = len(arr) - 1
    for k in range(end_num // 2, 0, -1):
        sink(Ary, k, end_num)

    while end_num > 1:
        Ary[1], Ary[end_num] = Ary[end_num], Ary[1]
        end_num -= 1
        sink(Ary, 1, end_num)


## test
arr = [0,  1, 5, 0, 5, 7, 7]
heap_sort(arr)
print(arr)