科幻小说作家们为何钟情质数?
科幻小说作家们为何钟情质数?
当科幻小说家想使书中的外星人和地球沟通时,他们往往会碰到一个难题。他们是要假定外星人极其聪明,从而能够轻易掌握地球语言呢,还是要假定他们已经发明出一种“宝贝鱼”[2]式的翻译软件,来帮助他们和地球进行沟通呢,或者,干脆设定宇宙中所有的外星人都讲英语呢?
[2] 雅虎的一款在线翻译工具, 与2012年下线——编者注
其中被许多作者采纳的一个解决方案是数学是唯一一门真正的宇宙语言,而且在这门语言中,所有人都应该先讲的几个词就是构成这门语言的基石——质数。在卡尔·萨根的小说《接触》中,为SETI(搜寻地外文明计划)工作的爱莉·埃洛维捕捉到一段信号,她意识到这段信号并不是背景噪音,而是一系列的脉冲。她猜测这些脉冲代表的是二进制的数字。通过将其转换为十进制后,她突然发现其中存在着一种模式:59、61、67、71……全是质数。随着信号的持续,她更加确信这一推测,质数列表一路攀升,一直到907。于是,她得出结论,这些信号不可能是随机的。有人正在向我们打招呼。
许多数学家都认为,即使宇宙的另一边存在着不同的生物学,不同的化学,甚至不同的物理学,但是,数学肯定是相同的。即使是围绕着织女星旋转的星球上生存的智慧生物,当他阅读一本讲述质数的数学书时,他仍将59和61视为质数。正如剑桥大学著名数学家戈弗雷·哈罗德·哈代所说的那样,这些数字之所以是质数,“并不是因为我们认为它们是质数,也不是因为人类特定的思维方式使然,而是因为它们本身就是质数,因为数学现实就是这么构建的”。
或许质数是整个宇宙都共通的数字,但是,我想知道类似于刚才我提及的那些故事是否在其他星球上也正在被讲述呢?这种想法还是很有趣的。数千年来,我们研究着这些数字,不断探索出关于这些数字的真相。而且,在发现这些真理的道路中,我们在每一个脚印中都能看到一种特别的文化印记以及历史上特定时期中的数学主旨。那么,在宇宙的其他文化中,是否也发现了另外一些不同的视角,使其探索出一些我们尚不知晓的理论呢?
在建议使用质数作为交流手段方面,卡尔·萨根不是第一个,也不会是最后一个。甚至,NASA(美国国家航空航天局)也试图利用质数来和地外智慧生物建立联系。1974年,他们就通过位于波多黎各的阿雷西波无线电望远镜朝着球状的M13星团方向发送了一段讯息。之所以选择M13星团,是因其恒星数量十分庞大,讯息被智慧体接收到的概率也会更大一些。
这段讯息包含一系列的数字0和1,它们可以被排列成一张黑白像素的图片。重构的图像中包含以下内容:二进制中从1到10的数字,一段DNA结构的素描,一段表示太阳系的图像,以及一幅阿雷西波无线电望远镜的图像。由于该图像中只包含1679个像素,因此,它的清晰度并不高。但是,选择1679这个数字也是有意为之的,因为其中隐含着重构这些像素的线索。因为1679=23×73,所以要在一个长方形中构建起这幅图像只有两种可能性。23行73列的排列方式会呈现出一片混乱的图像,而23列73行的方式则呈现出正确的图像。M13星团和我们地球之间的距离是25 000光年,因此,今天我们依然在漫长的等待中。就算能够收到回应,也至少要等上50 000年的时间!
图 1-5 阿雷西波无线电望远镜向M13星团发送的讯息
虽然质数是通用的,但人类书写质数的方式在整个数学史中经历了极大的变化,而且,这些书写方式与特定文化是密切相关的。接下来简短地回顾各大文化中质数的书写方式。
图 1-6
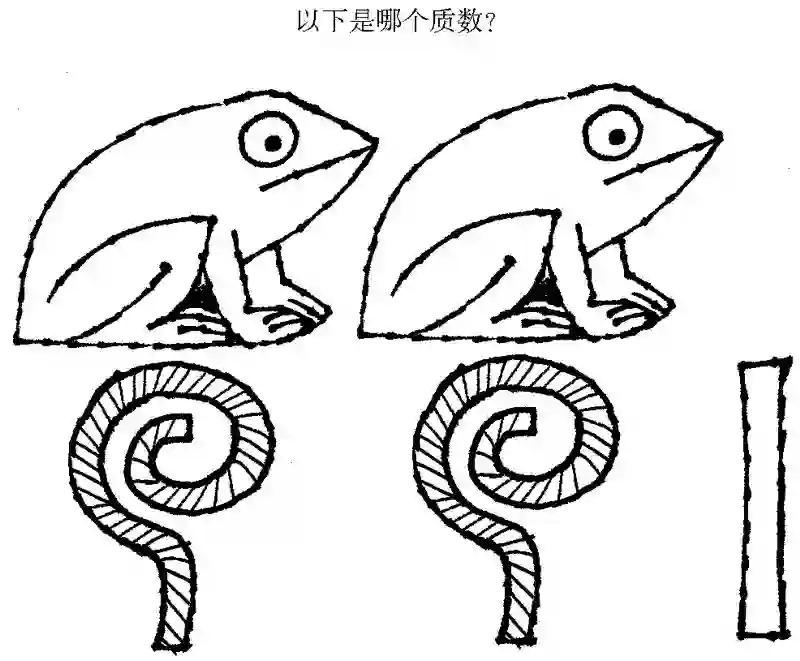
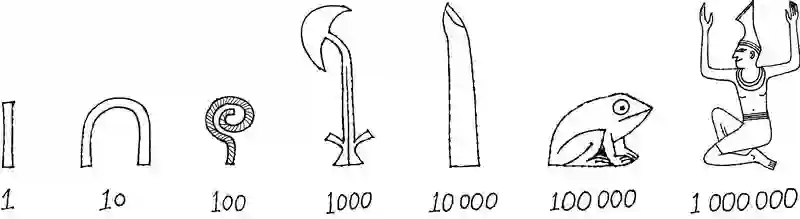
古埃及在早期的数学研究方面取得了一些成果,上图便是当时的人们书写200 201的方式。早在公元前6000年,古埃及人便放弃了游牧生活,开始定居在尼罗河沿岸。随着埃及社会日益成熟,人们在记录税收、测量土地和建造金字塔方面对数字的要求也越来越高。就像记载文字那样,埃及人也使用象形字来记载数字。基于10的幂数,他们建立了一套数字体系,如同我们今天使用的十进制系统。(之所以选择10,并非是因为该数字在数学上有特别的重要性,而仅仅是因为人体结构上的一个现实——人类共有10根手指。)不过,他们尚未发明位值体系,这也是书写数字的一种方式,其中每个数字的位置分别对应10的相应幂数。比如,222中的三个2根据它们各自的位置表示的数值也各不相同。事实上,古埃及人需要创造一些新符号来表示每个不同的10的幂数。
图 1-7 古埃及人对10的幂数的表述符号。其中,10是一根抽象的跟骨,100是一个绳圈,1000则是一棵睡莲
用这种象形字书写200 201这样的数字还算简单,但是,要用象形字书写质数9 999 991,就得罗列出55个符号。尽管古埃及人没有认识到质数的重要性,但他们还是发明了一些成熟的数学理论,包括计算金字塔体积的公式以及分数的概念,这也没什么大惊小怪的。不过他们标记数字的方式并不十分成熟,不同于他们的邻居古巴比伦人使用的 方式。
图 1-8
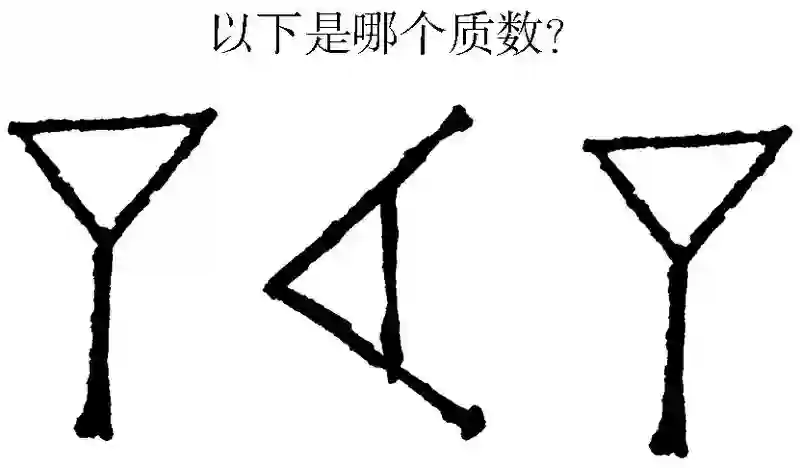
图1-8为古巴比伦人书写数字71的方式。和埃及帝国一样,巴比伦帝国也是栖息在一条大河——幼发拉底河周围。公元前1800年,古巴比伦人就控制了当今伊拉克、伊朗及叙利亚的大部分地区。为应付帝国的运营和扩张,古巴比伦人成为管理和掌控数字的大师。他们的文字均记载在泥版上,书写者使用木棍或尖刀在湿泥版上刻下信息,然后泥板会慢慢变干。书写用的刀尖呈V型或楔形,因此,今人也称巴比伦文字为楔形文字。
大约在公元前2000年左右,古巴比伦成为最早使用位值数字系统的文化之一。但是,不同于埃及人使用的10的幂数,古巴比伦人发明出一种基于60的数字系统。其中,从1到59均由不同的符号组合来表示,而当数字达到60时,他们会在数字左侧增加1位,代表整个60,这一点和十进制中当数字超过9时把1放置在十位上的道理相同。图1-8表示的质数包括1个60和1个表示11的符号,即71。其中,59以内的数字的表示符号也和十进制系统有一些潜在的联系,因为,从1到9的数字均由横线来表示,而10则由图1-9所示的符号表示。
图 1-9
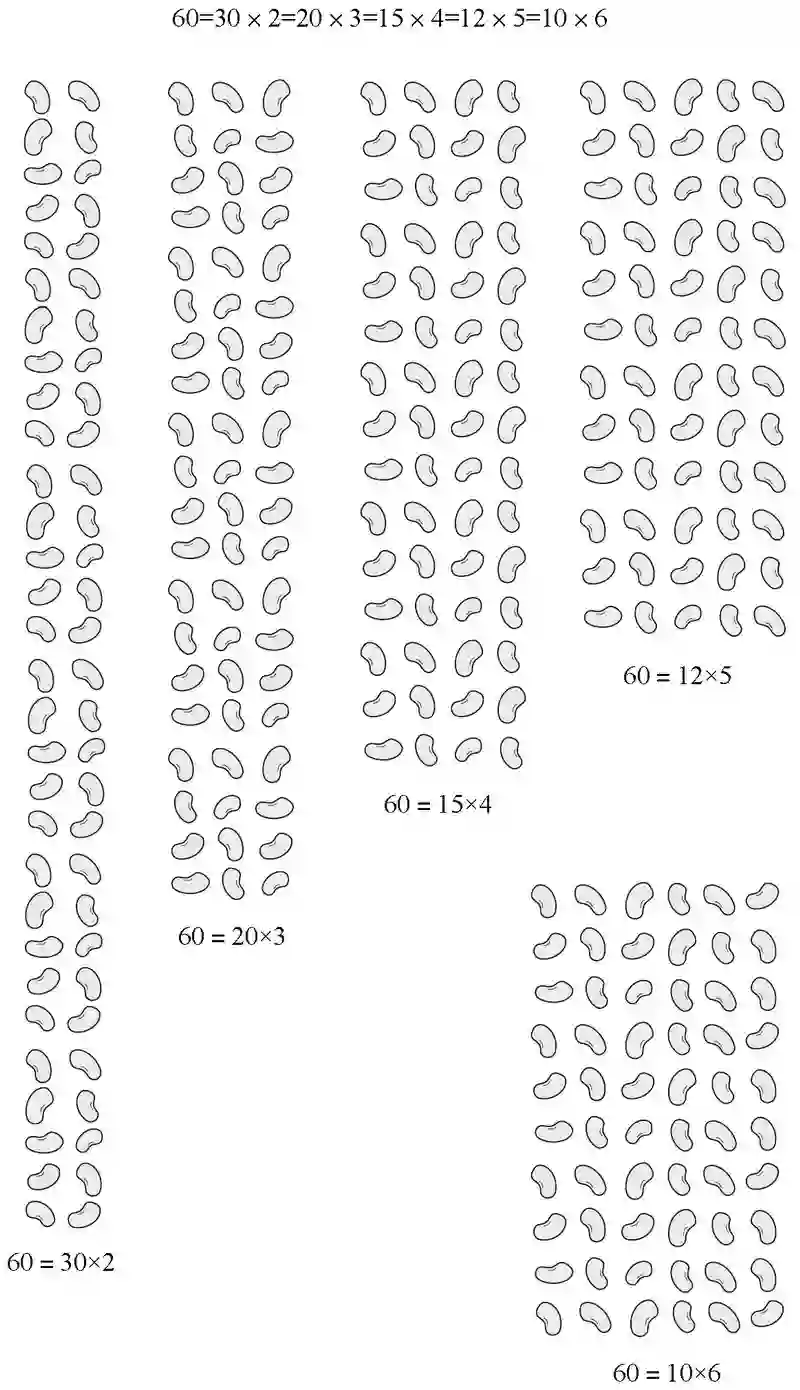
从数学角度看,以60作为底要比以10作为底更合理。60是个很容易拆分的数字,因此在计算方面会更加强大。比如有60颗豆子,我可以用多种不同方式把它们拆分开来:
图 1-10 拆分60颗豆子的不同方式
如何用手指数出60个数
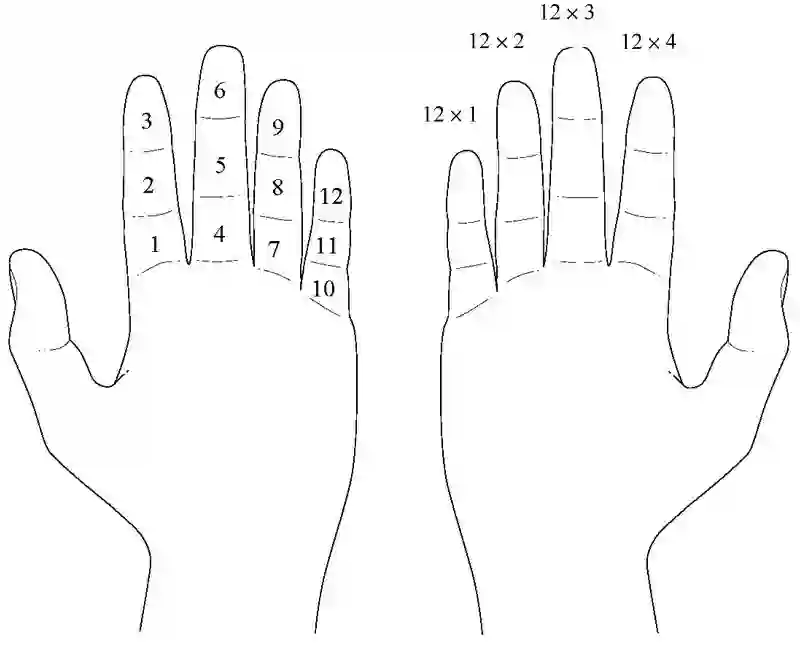
古巴比伦人选择的底数60在今天的世界中仍留有许多痕迹。比如,1分钟有60秒,1小时有60分钟,1个圆的360度=6×60度。证据显示,古巴比伦人曾以一种相当绝妙的方式,仅用手指便可以一直从1数到60。
我们都知道,人类除拇指外的每根手指均由3块骨头构成。而每只手上除拇指外有4根手指,拇指则可以指到另外4根手指上12块骨头中的任何一块。像这样地,左手可以从1数到12,右手的4根手指则用来表示你一共数过了多少个12(右手可数出4个12,加上左手4根手指上的一个12),这样,通过两只手的合作,我们就可以从1一直数到60了。
举个例子,要表示质数29,用右手的大拇指指向右手表示2个12的那根手指,左手的大拇指指向第5块骨头即可。
图 1-13
古巴比伦人离发现数学中一个十分重要的数字零只有一步之遥。人们用楔形文字书写数字3607时就会遇到一个麻烦。3607是3600,即60的平方,加上7,但是,如果我照此书写的话,结果就会像是一个60加上一个7,虽然67也是质数,但并非我要的那个。为解决这一问题,巴比伦人引入了一个小符号,用来标明该位置无需计数。于是,3607便被写成图1-12所示这样。
图 1-12
但他们并不把零本身当做一个数字。对他们来说,该符号只是用来表示位值系统中某个特定的60幂数的忽略不计。数学界要继续等待2700年的时间,直到进入公元7世纪,才由印度人首次引入了零这一数字,并对它的属性进行了探讨。古巴比伦人除发明书写数字的绝妙方式以外,还发现了第一个二次方程的解法,今天,每个孩子在学校都会学到这种解方程的方法。另外,对于有关直角三角形的毕达哥拉斯定理,他们也是最早的认识者。但并没有证据显示古巴比伦人知道质数的美妙所在。
图 1-13
中美洲的玛雅文明于公元200到900年间达到巅峰。整个文明从墨西哥南部一直延伸到危地马拉和萨尔瓦多。为了支持他们高超的天文运算能力,该文明发展出了一种十分成熟的数字系统,图1-13便是使用该系统书写的数字17。和古埃及人以及古巴比伦人不同的地方在于,玛雅人采用的是一个以20为底的数字系统。他们用1点表示1,2点表示2,3点表示3,就像囚犯在墙上画线数日子一样,当写到5时,不再点下第五个点,而是画一条线贯穿之前的那4个点。如此,一条直线便表示数字5。
该系统是依据人类大脑能够快速分辨出较小数量这一特性而设定的,这一点的确十分有趣。我们能很快分辨出一个两个三个四个,但数量再多下去,判断就越来越难了。当玛雅人数到19(3条线4个点)后,他们便创造出一个新的位数来表示20的倍数。而再后面一位,按规律应该用来表示400(20×20)的倍数,但奇怪的是,这位数字却被用来表示360(20×18)的倍数。这种奇怪的安排源于玛雅历。在玛雅历中,一年包含18个月,一个月包含20天。(这样算下来一年只有360天。为了补足差的那5天,玛雅人又增加了一个月份来囊括这5个“坏日子”,这5天被视为凶日。)
有趣的是,和古巴比伦人一样,玛雅人也是用一个特殊符号来表示20的某个特定幂数的忽略不计。该数字系统中的每一位都关联着一位神祗,而每个位置上如果没有放置符号则被认为是对神祗的不敬。因此,玛雅人选择用一幅贝壳图画来表示空。关于该符号的创造,既有数学原因,也有玛雅人的迷信考量。和古巴比伦人相同的是,玛雅人也并未将零本身视为一个独立数字。
由于玛雅人的天文计算涉及漫长的时间周期,他们因此需要一种能够表示庞大数字的系统。其中一个时间周期是通过所谓的长计历来衡量的,该历法起始于公元前3114年的8月11日,使用5位数来计量,因此最长可计算20×20×20×18×20天,即整整7890年。2012年12月21日在玛雅历中是一个重要的日子,在这一天,玛雅历将走到13.0.0.0.0。就像汽车后座上的孩子等待汽车里程表“溢出”复零的那一刻,如今危地马拉人也开始为这一天的到来而兴奋,尽管在一些末日论者的眼中,这一天将是世界毁灭之日。
虽然下方图中都是字母而非数字,但这就是希伯来语中13的书写方式。在古犹太的根码替亚释义法传统中,希伯来字母表中的每个字母都有一个数字值。图1-14中,gimel是第三个字母,yodh是第十个字母。于是,将这两个字母组合起来便代表数字13。
图 1-14
虽然质数在希伯来文化中并未凸显出其重要性,但与质数相关的数字的重要性还是被凸显了出来。拿来一个数字,考察所有能整数它的数字(原数字除外)。如果这些因子相加以后正好得出最初那个数字,那么,该数字便被称为完全数。6是第一个完全数,除6本身以外,它能够分解出的乘法因子包括1、2和3。这三个数字全部加起来就能得到数字6。第二个完全数为28。28的乘法因子包括1、2、4、7和14,这些数字相加之后又得到28。根据犹太人的宗教信仰,世界是在6天内被创造出来的,而在犹太历中的阴历月份中,每个月只有28天。这一现象在犹太文化中发酵,他们相信完全数都具有特殊含义。
这些完全数的数学和宗教属性同样也得到了基督教评论者的注意。圣奥古斯丁(354—430)在他著名的《上帝之城》中写道:“6本身就是个完全数,并非因为上帝在6天内创造了一切。反过来说才是准确的,上帝之所以在6天内创造一切,正是因为该数字是完美的。”
有趣的是,这些完全数背后隐藏着质数的踪迹。每个完全数都对应着一个被称为梅森质数的特殊质数(本章稍后会详细介绍)。迄今为止,我们只知道47个完全数,其中最大的一个共有25 956 377位。这些完全数都是偶数,并且都可分解成2^(n-1)(2^n-1)。而且只要当2^(n-1)(2^n-1)是一个完全数时,其中的(2^n-1)必为质数,反之亦然。我们尚未发现任何一个为奇数的完全数。
你可能认为图1-15表示的是质数5,它看上去非常像2+3。但实际上,中间的符号并非加号,而是中文里的数字10。以上三个数字放在一起表示两个10加上3,即23。
图 1-15
这种传统的中文书写方式并未使用位值体系,而是为每个不同的10的幂数提供一个符号。但在另外一种用竹签记数的系统中则采用了位值体系。这一系统是从算盘演化而来的。在算盘中,每当前一列里的数字超过10时,便另起一列。
图1-16所示是用竹签记数的系统中数字1到9所对应的符号。
图 1-16
为避免混淆,每隔一位(十位、千位、十万位……),他们会把数字翻个个,使竹签竖过来。如图1-17所示。
图 1-17
古代的中国人甚至有了负数的概念,正负数分别由不同颜色的竹签来表示。西方对于红黑墨水的使用据说正是来自于中国人对于红黑竹签的运用,但有趣的是,中国人用黑色竹签表示负数。
中国文化可能是最早认识到质数重要性的文化之一。中国人认为每个数字都有性别,偶数为阴,奇数为阳。他们还意识到某些奇数尤其特别。例如,如果有15块石头,你可以用三排五列的方式将其摆成一个规则的长方形;但如果有17块石头,则无法进行这样的排列,你只能将所有石头摆成一条直线。因此,对中国人来说,质数是一些最具阳刚气概的数字。而其他那些非质数的奇数,尽管也是阳性,但多少有些阴柔气质。
这一古中国人的视角捕捉到了质数最本质的属性——若无法将一堆石头排列为一个整齐的长方形的话,那么,石头的数量便为质数。
综上所述,我们了解到古埃及人用青蛙图片来描述数字,古玛雅人使用点和线,古巴比伦人在粘土板上刻字,古中国人排列竹签,而在希伯来文明中,字母中则包含着数字含义。虽然古代中国或许是首个认识到质数重要性的文明,但真正揭示出这些神秘数字神奇之处的则是另外一个文明——古希腊。(待续)
上文节选自《神奇的数学》, 已获人邮图灵授权许可, [遇见数学] 特此表示感谢!
神奇的数学:
牛津教授给青少年的讲座
遇见数学, 遇见更精彩的自己
非常感谢您的关注和支持!