可以管理时间的二叉堆

来自：码分享，作者： 涛声依旧

面试官：写一个堆排吧

我心想：堆排是什么鬼

理解堆排，首先要理解二叉堆。理解了二叉堆的“下沉”操作，基本上就可以理解堆排了。今天我们来看一看什么是堆，以及堆的一般操作

优先级队列

近日，谦子遇到了烦心事，于是找老师去诉苦了

老师，最近好烦啊

谦子

克

哦，怎么了？

最近感觉好多事，前一天晚上计划好的事第二天总是乱套

谦子

克

怎么讲？

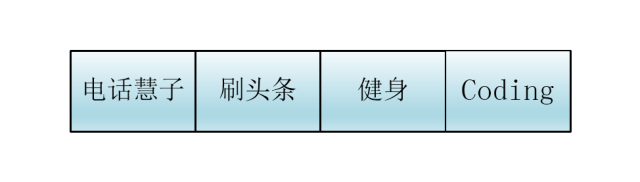
比如昨天吧，前天计划好要Coding两小时、健身一小时...

谦子

谦子列了几个要做的事

可是到了第二天，Coding的时候，室友让我来一把荒野行动，刷头条的时候女朋友又打来电话，到头来啥都没弄好

谦子

谦子道出了心中的苦

克

这个其实好办，首先你心里对每件事都要有一个“重要的程度”，就称为优先级吧，你可以优先级高的先做，低的后做

谦子两眼发光

克

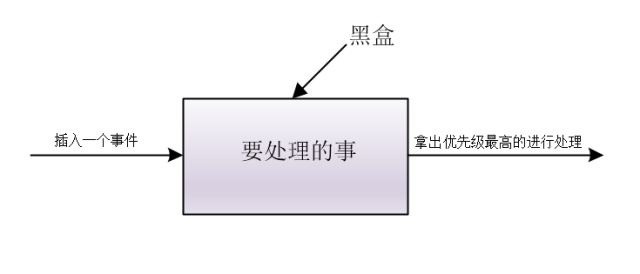
你可以做优先级最高的事情，做完后删除它，然后做剩下优先级最高的事，当然，很有可能有其他事插入进来，新插入的事情如果优先级不是最高，就不做，这样你就一直做优先级最高的事了

克顺手画了一个图

请输入

这个支持删除最大元素和插入元素的数据结构其实就是我们计算机中的优先级队列

优先级队列中每个元素都有优先级

优先级最高的最先被处理

优先级队列的实现

哦，那这个优先级队列是如何实现的呢？

谦子

谦子非常想知道黑盒里面是什么

克

如果是你，你会怎么实现？

克非常善于引导学生思考

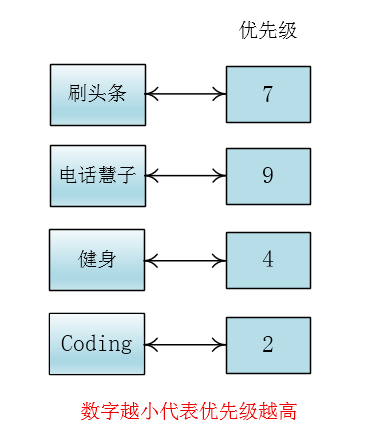
我首先会把优先级和事情一一对应起来，优先级用整数来表示

谦子

谦子想了想说

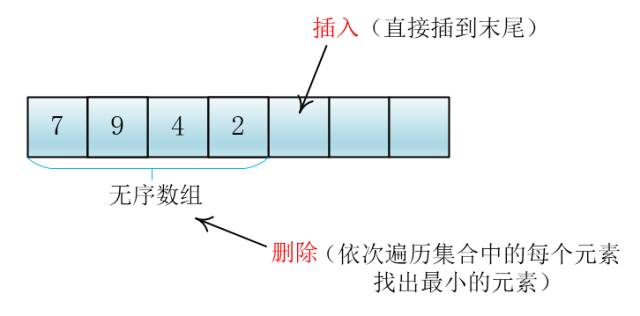
然后我把优先级存入一个无序数组里，取出的时候遍历数组一边，找出最小值，插入的时候直接插到集合末尾

谦子

谦子说着说着画了一个图

这样就可以实现取出（删除）优先级最高的元素以及支持插入操作了

谦子

克

你这个虽然插入元素很快，但是删除元素却很慢（时间复杂度O(N)）,再想想

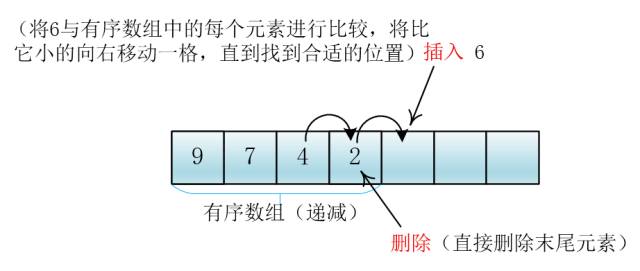
那我可以每插入一个元素后都使整个数组中的元素有序，删除的时候直接删除数组中最后一个元素

克

谦子画了一幅图解释道

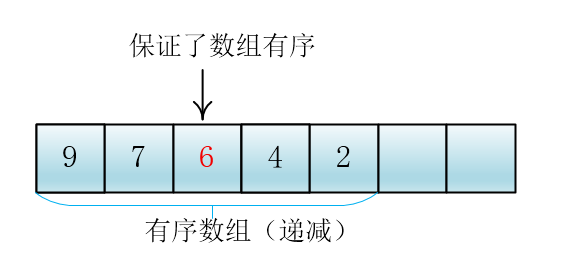
随后，谦子又画出了插入6后的图

克

你这个虽然删除元素非常高效，但是插入特别费时（时间复杂度也为O(N)）

克还是不满意

还有插入和删除都高效的办法吗？

谦子

克

有的，那就是堆

堆

哦！堆是什么？

谦子

克

要了解堆（二叉堆），我们先看看完全二叉树

这里我们只讨论二叉堆，把二叉堆称为堆

堆也有d-堆，左式堆等等

克

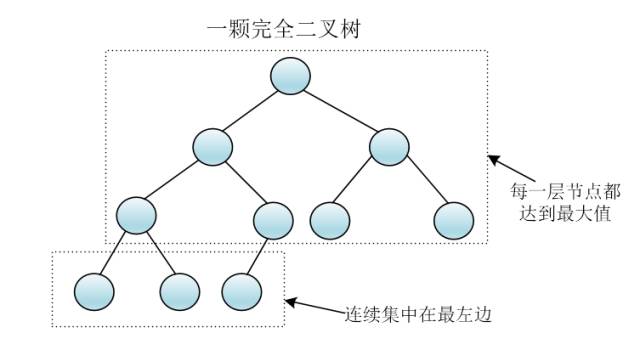
所谓完全二叉树，简单来说，就是除了最后一层外每一层节点数均达到最大值，并且最后一层的节点都连续集中在最左边

克看谦子不是很明白，顺手画了个图

克

如果对于每个父节点的值都大于等于（或者小于等于）其两个孩子的值，那么就称这种特殊的数据结构为堆（这个条件也被称作堆有序性）

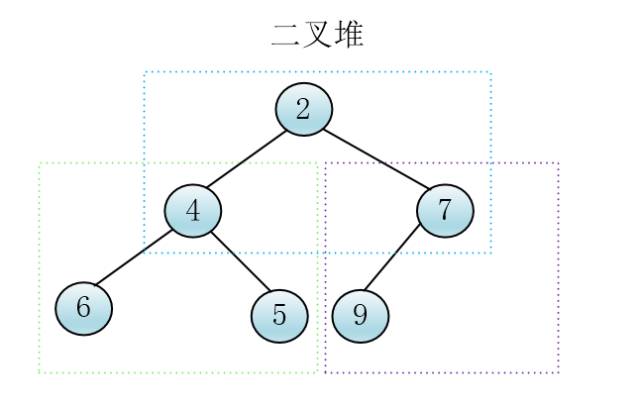
克画了一个二叉堆实例

克

看到了吧，这是父节点小于等于两个孩子的情况，当然也有大于等于两个孩子的情况

注意：二叉堆中两个孩子之前的大小没有关系，可能左孩子>=右孩子，也可能右>=左

克

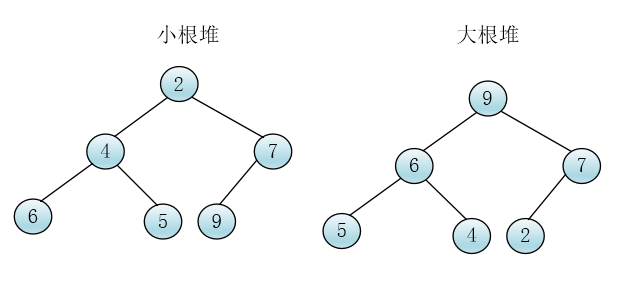
刚才父节点小于等于两个孩子的情况我们称之为小跟堆，反之，我们称为大根堆

克随手画了一个小根堆和一个大根堆

本文讨论小根堆

哦，那这个就用链表来存储了

谦子

克

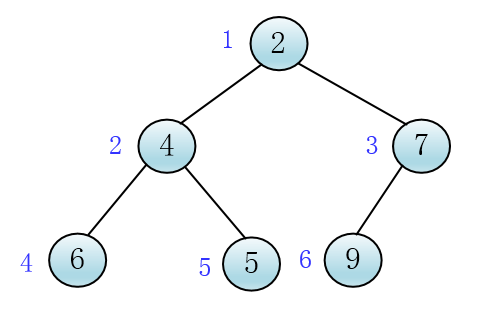
这个用数组来存储岂不更好，根节点标记为1，从上到下每层按从左到右的顺序标记每个节点

克

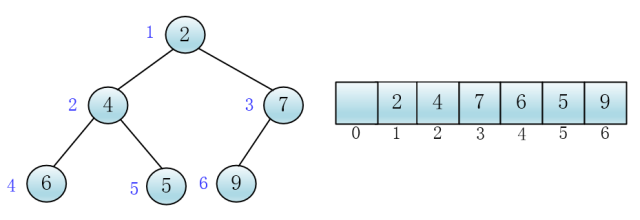
然后将元素存入对应下标的数组中

克

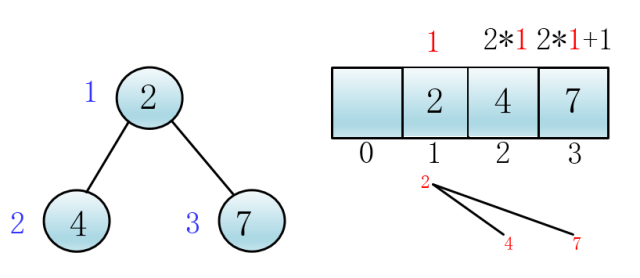
这样，父子关系就可以用下标来表示了，显然，在k下标处的节点的左孩子一定在2*k小标处，右孩子在2*k+1处

克

显然，k位置的父亲是k/2

堆我懂了，那对于插入和删除这个堆该怎么做呢？

谦子

插入操作

克

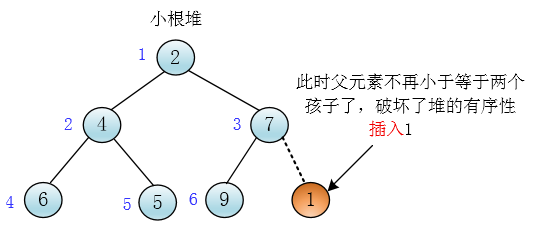
当你插入一个元素的时候，很有可能破坏堆的有序性

每个父节点的值小于等于其左右孩子的值被称为堆的有序性

另一种情况是大于等于也称之为堆的有序性

克随手画了一个插入操作破坏堆有序性的图

克

很显然此时我们要调整堆使之恢复堆的有序性

如何调整，谦子心里想

克

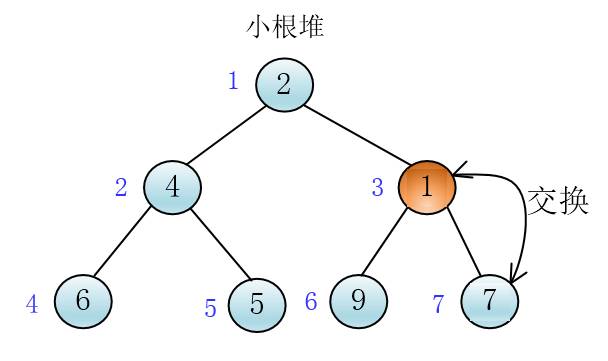
很容易可以想到，可以将1和它的父比较，如果小于其父，那就交换两个节点的值

克

此时1和父节点7交换了，我们称这个过程为“上浮”

上浮这个词形象生动，谦子心里想

克

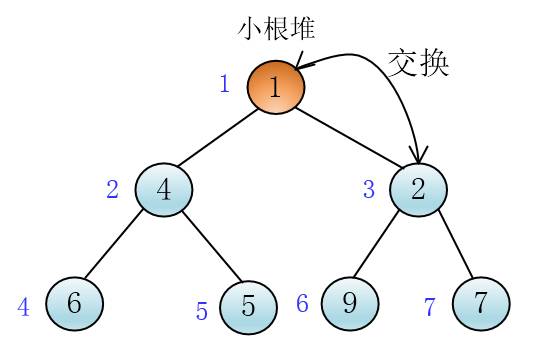
这个时候1成为了2的右孩子了，此时它比2小，还得继续交换

克

此时，整个插入过程就完成了

说完，克飞速地写出了上浮的代码

谦子暗自惊叹老师的代码功力

删除操作

克

插入操作已经给你演示过了，删除操作你来想想吧

谦子听完此话紧张的手心出汗，但还是硬着头皮想了想，突然灵光一现

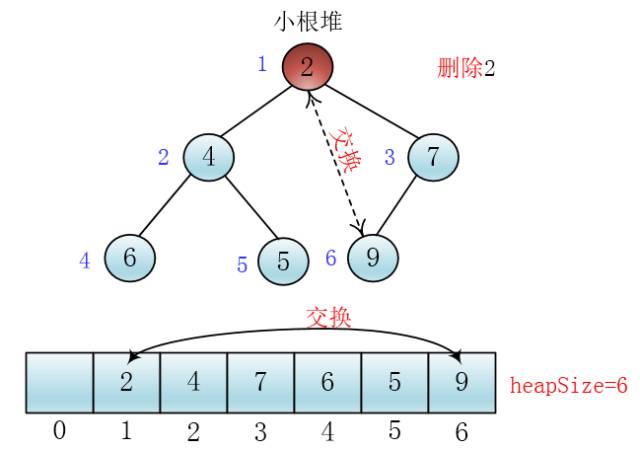
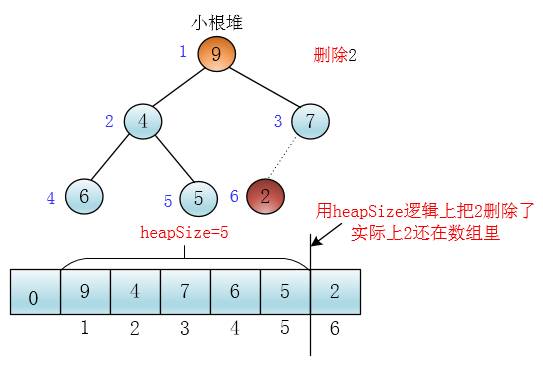
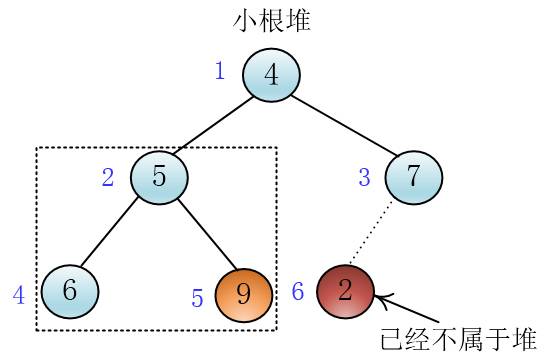
我可以把堆顶的元素和堆的最后一个元素交换，然后逻辑上删除最后一个元素

谦子

这里我用一个heapSize变量记录堆中元素的个数，交换后heapSize减一

谦子

随后谦子画出了交换后的图

这样我就通过交换堆顶元素与最后一个元素和heapSize减一把堆顶元素删除了

谦子

克

这个思路挺好，但是当你交换元素后，交换后的堆就不满足堆有序了？你该怎么办？

与插入相对应，我可以将堆顶这个元素向下沉

谦子

克

哦，具体怎么做

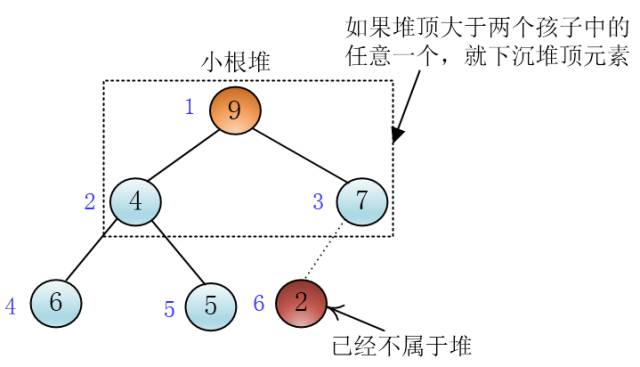
当堆顶元素大于两个孩子中的任意一个，我就下沉堆顶元素，直到堆顶元素小于等于它的两个孩子

谦子

克

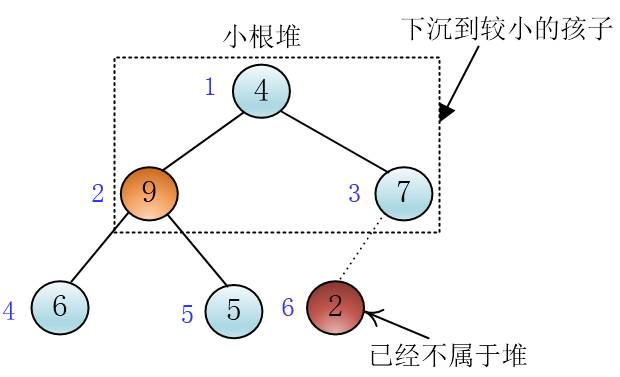
下沉到哪个孩子

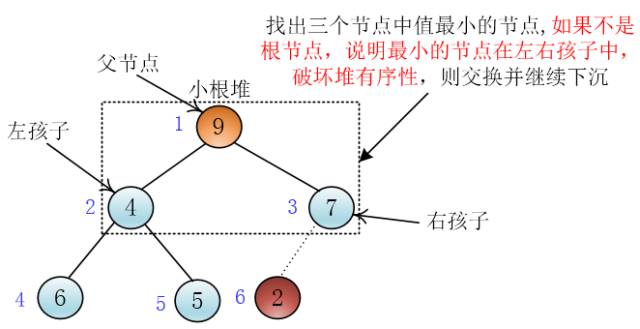
当然是两个孩子中最小的那一个，因为最小的那个要上浮到堆顶

谦子

这个时候堆顶元素9来到了它的左孩子处，但是此时它大于现在的左右孩子

谦子

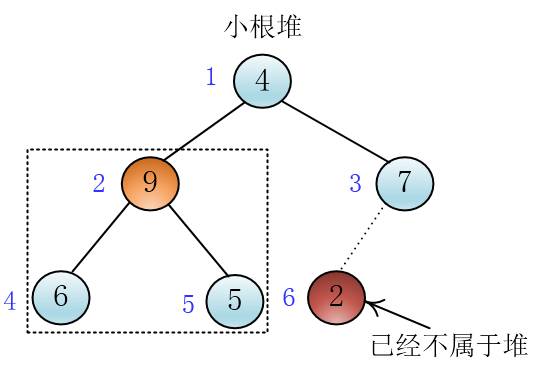
所以要继续下沉

谦子

此时下沉完毕

谦子

克

很不错，完全正确，这就是堆下沉的整个操作，那你写一下这个操作的代码吧

谦子刚松了口气，谁知还要写代码，只见谦子想了想，写写擦擦好几遍最终写下了如下代码

我找出以要下沉节点为父节点和它的左右孩中值最小的节点，如果该节点是左右孩子其中一个，则下沉，否则不下沉

谦子

慧子解释道，并画了一个图

克

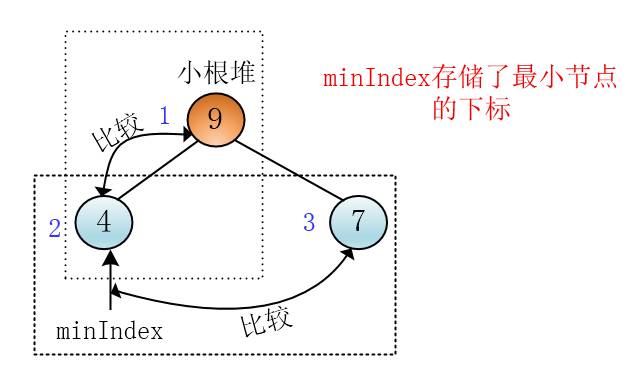
这个思路不错，那你的那个找出最小节点下标的函数(minIndex())是如何实现的？

只见谦子又写了一段代码

leftIndex = 2*parentIndex;

rightIndex = 2*parentIndex+1;

我用一个变量存储值最小节点的下标，先让左孩子和父节点比，将其中值小的节点的下标存入minIndex，然后让右孩子与刚才选出最小值的节点比，更新minIndex

谦子

克

恩恩，不错，好了，堆这块就到这

好的，感谢老师解惑

谦子

看来以后得好好学数据结构与算法了，不然连时间都管理不好，谦子心想

---

●本文编号534，以后想阅读这篇文章直接输入534即可

●输入m获取文章目录

推荐↓↓↓

 

Java编程

更多推荐《18个技术类微信公众号》

涵盖：程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。