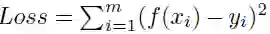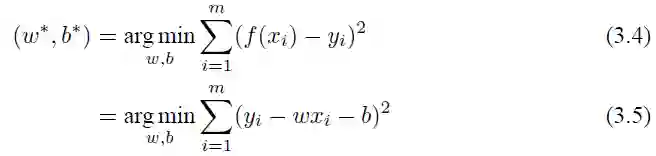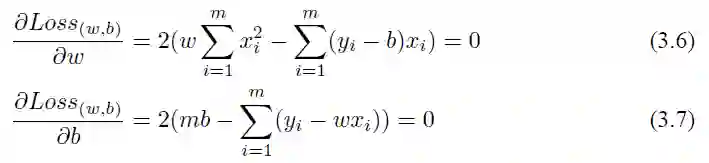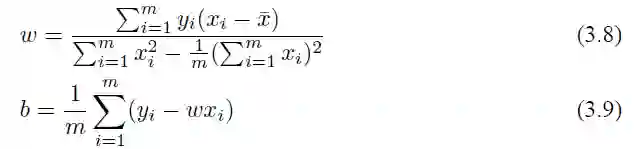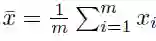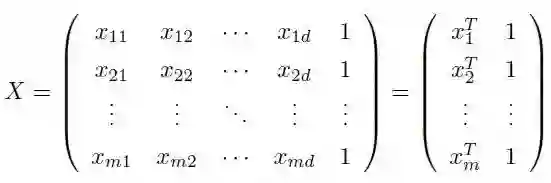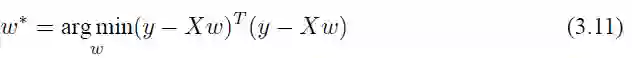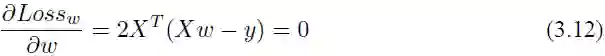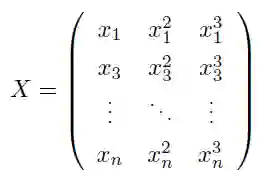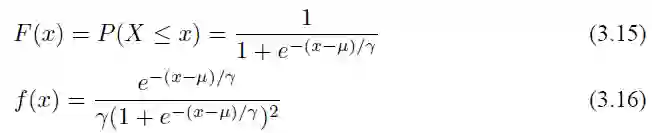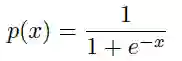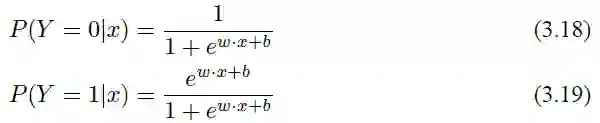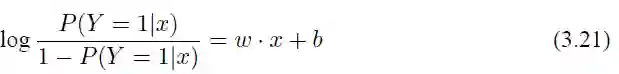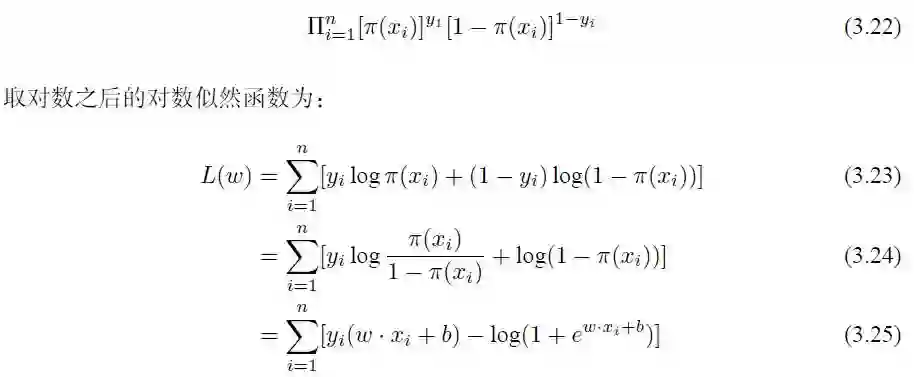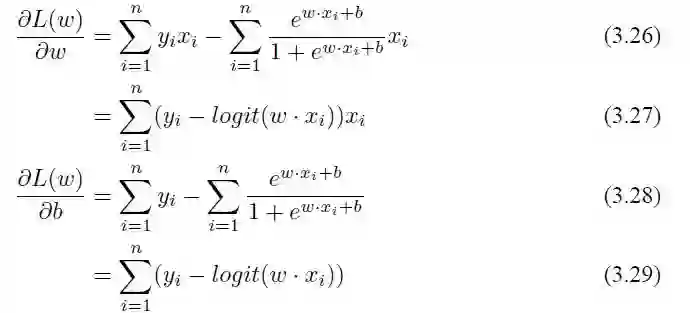送书 | 从零开始学习 PyTorch：多层全连接神经网络

2017 年 12 月 1 日 AI100 福利菌

本文引自博文视点新书《深度学习入门之PyTorch》第3 章——多层全连接神经网络

内容提要：深度学习如今已经成为科技领域最炙手可热的技术，在《深度学习入门之PyTorch》中，我们将帮助你入门深度学习。《深度学习入门之PyTorch》将从机器学习和深度学习的基础理论入手，从零开始学习 PyTorch，了解 PyTorch 基础，以及如何用 PyTorch 框架搭建模型。通过阅读《深度学习入门之PyTorch》，你将学到机器学习中的线性回归和 Logistic 回归、深度学习的优化方法、多层全连接神经网络、卷积神经网络、循环神经网络，以及生成对抗网络，最后通过实战了解深度学习前沿的研究成果，以及 PyTorch 在实际项目中的应用。《深度学习入门之PyTorch》将理论和代码相结合，帮助读者更好地入门深度学习，适合任何对深度学习感兴趣的人阅读。

参与方式：喜欢这本书，请在评论区留言，和大家分享你对PyTorch的使用经验和心得，根据评论质量和评论点赞数，前五名同学可获得本书。活动截止时间为12月4日（下周一22点）

深度学习的前身便是多层全连接神经网络，神经网络领域最开始主要是用来模拟人脑神经元系统，但是随后逐渐发展成了一项机器学习技术。多层全连接神经网络是现在深度学习中各种复杂网络的基础，了解它能够帮助我们更好地学习之后的内容。这一章我们将先从 PyTorch 基础入手，介绍 PyTorch 的处理对象、运算操作、自动求导，以及数据处理方法，接着从线性模型开始进入机器学习的内容，然后由 Logistic回归引入分类问题，接着介绍多层全连接神经网络、反向传播算法、各种基于梯度的优化算法、数据预处理和训练技巧，最后用 PyTorch 实现多层全连接神经网络。

3.1 热身：PyTorch 基础

首先我们会介绍一下 PyTorch 里面的一些基础知识，有了这些基础知识之后我们才能做出更多复杂的变形。

3.1.1 Tensor（张量）

PyTorch 里面处理的最基本的操作对象就是 Tensor，Tensor 是张量的英文，表示的是一个多维的矩阵，比如零维就是一个点，一维就是向量，二维就是一般的矩阵，多维就相当于一个多维的数组，这和 numpy 是对应的，而且 PyTorch 的 Tensor 可以和 numpy的 ndarray 相互转换，唯一不同的是 PyTorch 可以在 GPU 上运行，而 numpy 的 ndarray只能在 CPU 上运行。

我们先介绍一下一些常用的不同数据类型的 Tensor，有 32 位浮点型 torch.FloatTensor、64 位浮点型 torch.DoubleTensor、16 位整型 torch.Shor tTensor、32 位整型 torch.IntTensor 和 64 位整型 torch.LongTensor。我们可以通过下面这样的方式来定义一个三行两列给定元素的矩阵，并且显示出矩阵的元素和大小：

a = torch.Tensor([[2, 3], [4, 8], [7, 9]])

print('a is: {}'.format(a))

print('a size is {}'.format(a.size())) # a.size() = 3, 2

需要注意的是 torch.Tensor 默认的是 torch.FloatTensor 数据类型，也可以

定义我们想要的数据类型，就像下面这样：

b = torch.LongTensor([[2, 3], [4, 8], [7, 9]])

print('b is : {}'.format(b))

当然也可以创建一个全是 0 的空 Tensor 或者取一个正态分布作为随机初始值：

c = torch.zeros((3, 2))

print('zero tensor: {}'.format(c))

d = torch.randn((3, 2))

print('normal randon is : {}'.format(d))

我们也可以像 numpy 一样通过索引的方式取得其中的元素，同时也可以改变它的值，比如将 a 的第一行第二列改变为 100。

a[0, 1] = 100

print('changed a is: {}'.format(a))

除此之外，还可以在 Tensor 与 numpy.ndarray 之间相互转换：

numpy_b = b.numpy()

print('conver to numpy is \n {}'.format(numpy_b))

e = np.array([[2, 3], [4, 5]])

torch_e = torch.from_numpy(e)

print('from numpy to torch.Tensor is {}'.format(torch_e))

f_torch_e = torch_e.float()

print('change data type to float tensor: {}'.format(f_torch_e))

通过简单的 b.numpy()，就能将 b 转换为 numpy 数据类型，同时使用 torch.from_num py() 就能将 numpy 转换为 tensor，如果需要更改 tensor 的数据类型，只需要在转换后的 tensor 后面加上你需要的类型，比如想将 a 的类型转换成 float，只需 a.float()就可以了。

如果你的电脑支持 GPU 加速，还可以将 Tensor 放到 GPU 上。首先通过 torch.cuda.is_available() 判断一下是否支持 GPU，如果想把 tensora 放到 GPU 上，只需 a.cuda() 就能够将 tensor a 放到 GPU 上了。

if torch.cuda.is_available():

a_cuda = a.cuda()

print(a_cuda)

3.1.2 Variable（变量）

接着要讲的一个概念就是 Variable，也就是变量，这个在 numpy 里面就没有了，是神经网络计算图里特有的一个概念，就是 Variable 提供了自动求导的功能，之前如果了解过 Tensorflow 的读者应该清楚神经网络在做运算的时候需要先构造一个计算图谱，然后在里面进行前向传播和反向传播。

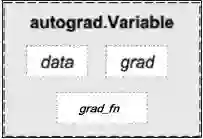
Variable 和 Tensor 本质上没有区别，不过 Variable 会被放入一个计算图中，然后进行前向传播，反向传播，自动求导。首先 Variable 是在 torch.autograd.Variable 中，要将一个 tensor 变成 Variable也非常简单，比如想让一个 tensor a 变成 Variable，只需要 Variable(a) 就可以了。我们可以通过图 3.1了解到 Variable 的属性。

图 3.1 结构图

从图3.1中可以看出 Variable 有三个比较重要的组成属性：data，grad 和 grad_fn。通过 data 可以取出 Variable 里面的 tensor 数值，grad_fn 表示的是得到这个 Variable 的操作，比如通过加减还是乘除来得到的，最后 grad 是这个 Variabel 的反向传播梯度，下面通过例子来具体说明一下：

# Create Variable

x = Variable(torch.Tensor([1]), requires_grad=True)

w = Variable(torch.Tensor([2]), requires_grad=True)

b = Variable(torch.Tensor([3]), requires_grad=True)

# Build a computational graph.

y = w * x + b # y = 2 * x + 3

# Compute gradients

y.backward() # same as y.backward(torch.FloatTensor([1]))

# Print out the gradients.

print(x.grad) # x.grad = 2

print(w.grad) # w.grad = 1

print(b.grad) # b.grad = 1

构建 Variable，要注意得传入一个参数 requires_grad=True，这个参数表示是否对这个变量求梯度，默认的是 False，也就是不对这个变量求梯度，这里我们希望得到这些变量的梯度，所以需要传入这个参数。从上面的代码中，我们注意到了一行 y.backward()，这一行代码就是所谓的自动求导，这其实等价于 y.backward(torch.FloatTensor([1]))，只不过对于标量求导里面的参数就可以不写了，自动求导不需要你再去明确地写明哪个函数对哪个函数求导，直接通过这行代码就能对所有的需要梯度的变量进行求导，得到它们的梯度，然后通过 x.grad 可以得到 x 的梯度。

上面是标量的求导，同时也可以做矩阵求导，比如：

x = torch.randn(3)

x = Variable(x, requires_grad=True)

y = x * 2

print(y)

y.backward(torch.FloatTensor([1, 0.1, 0.01]))

print(x.grad)

相当于给出了一个三维向量去做运算，这时候得到的结果 y 就是一个向量，这里对这个向量求导就不能直接写成 y.backward()，这样程序是会报错的。这个时候需要传入参数声明，比如 y.backward(torch.FloatTensor([1, 1, 1]))，这样得到的结果就是它们每个分量的梯度，或者可以传入 y.backward(torch.FloatTensor([1,0.1, 0.01]))，这样得到的梯度就是它们原本的梯度分别乘上 1，0.1 和 0.01。

3.1.3 Dataset（数据集）

在处理任何机器学习问题之前都需要数据读取，并进行预处理。PyTorch 提供了很多工具使得数据的读取和预处理变得很容易。

torch.utils.data.Dataset 是代表这一数据的抽象类，你可以自己定义你的数

据类继承和重写这个抽象类，非常简单，只需要定义__len__和__getitem__这两个函数：

class myDataset(Dataset):

def __init__(self, csv_file, txt_file, root_dir, other_file):

self.csv_data = pd.read_csv(csv_file)

with open(txt_file, 'r') as f:

data_list = f.readlines()

self.txt_data = data_list

self.root_dir = root_dir

def __len__(self):

return len(self.csv_data)

def __getitem__(self, idx):

data = (self.csv_data[idx], self.txt_data[idx])

return data

通过上面的方式，可以定义我们需要的数据类，可以通过迭代的方式来取得每一个数据，但是这样很难实现取 batch，shuffle 或者是多线程去读取数据，所以 PyTorch中提供了一个简单的办法来做这个事情，通过 torch.utils.data.DataLoader 来定义一个新的迭代器，如下：

dataiter = DataLoader(myDataset, batch_size=32, shuffle=True,

collate_fn=default_collate)

里面的参数都特别清楚，只有 collate_fn 是表示如何取样本的，我们可以定义

自己的函数来准确地实现想要的功能，默认的函数在一般情况下都是可以使用的。

另外在 torchvision 这个包中还有一个更高级的有关于计算机视觉的数据读取类：ImageFolder，主要功能是处理图片，且要求图片是下面这种存放形式：

root/dog/xxx.png

root/dog/xxy.png

root/dog/xxz.png

root/cat/123.png

root/cat/asd.png

root/cat/zxc.png

之后这样来调用这个类：

dset = ImageFolder(root='root_path', transform=None,loader=default_loader)

其中的 root 需要是根目录，在这个目录下有几个文件夹，每个文件夹表示一个类别：transform 和 target_transform 是图片增强，之后我们会详细讲；loader 是图片读取的办法，因为我们读取的是图片的名字，然后通过 loader 将图片转换成我们需要的图片类型进入神经网络。

3.1.4 nn.Module（模组）

在 PyTorch 里面编写神经网络，所有的层结构和损失函数都来自于 torch.nn，所有的模型构建都是从这个基类 nn.Module 继承的，于是有了下面这个模板。

class net_name(nn.Module):

def __init__(self, other_arguments):

super(net_name, self).__init__()

self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size)

# other network layer

def forward(self, x):

x = self.conv1(x)

return x

这样就建立了一个计算图，并且这个结构可以复用多次，每次调用就相当于用该计算图定义的相同参数做一次前向传播，这得益于 PyTorch 的自动求导功能，所以我们不需要自己编写反向传播，而所有的网络层都是由 nn 这个包得到的，比如线性层nn.Linear，等之后使用的时候我们可以详细地介绍每一种网络对应的结构，以及如何调用。

定义完模型之后，我们需要通过 nn 这个包来定义损失函数。常见的损失函数都已经定义在了 nn 中，比如均方误差、多分类的交叉熵，以及二分类的交叉熵，等等，调用这些已经定义好的损失函数也很简单：

criterion = nn.CrossEntropyLoss()

loss = criterion(output, target)

这样就能求得我们的输出和真实目标之间的损失函数了。

3.1.5 torch.optim（优化）

在机器学习或者深度学习中，我们需要通过修改参数使得损失函数最小化（或最大化），优化算法就是一种调整模型参数更新的策略。

优化算法分为两大类。

1. 一阶优化算法

这种算法使用各个参数的梯度值来更新参数，最常用的一阶优化算法是梯度下降。所谓的梯度就是导数的多变量表达式，函数的梯度形成了一个向量场，同时也是一个方向，这个方向上方向导数最大，且等于梯度。梯度下降的功能是通过寻找最小值，控制方差，更新模型参数，最终使模型收敛，网络的参数更新公式是：

其中 η 是学习率，是函数的梯度，我们可以通过图 3.2形象地说明一下该方法。这是深度学习里面最常用的优化方法，我们之后会详细讲解它的各种变式。

2. 二阶优化算法

二阶优化算法使用了二阶导数（也叫做 Hessian 方法）来最小化或最大化损失函数，主要基于牛顿法，但是由于二阶导数的计算成本很高，所以这种方法并没有广泛使用。torch.optim 是一个实现各种优化算法的包，大多数常见的算法都能够直接通过这个包来调用，比如随机梯度下降，以及添加动量的随机梯度下降，自适应学习率等。

在调用的时候将需要优化的参数传入，这些参数都必须是 Variable，然后传入一些基本的设定，比如学习率和动量等。

图 3.2 一阶优化算法

下面举一个例子：

optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

这样我们就将模型的参数作为需要更新的参数传入优化器，设定学习率是 0.01，动量是 0.9 的随机梯度下降，在优化之前需要先将梯度归零，即 optimizer.zeros()，然后通过 loss.backward() 反向传播，自动求导得到每个参数的梯度，最后只需要optimizer.step() 就可以通过梯度做一步参数更新。

3.1.6 模型的保存和加载

在 PyTorch 里面使用 torch.save 来保存模型的结构和参数，有两种保存方式：

（1）保存整个模型的结构信息和参数信息，保存的对象是模型 model；

（2）保存模型的参数，保存的对象是模型的状态 model.state_dict()。

可以这样保存，save 的第一个参数是保存对象，第二个参数是保存路径及名称：

torch.save(model, './model.pth')

torch.save(model.state_dict(), './model_state.pth')

加载模型有两种方式对应于保存模型的方式：

（1）加载完整的模型结构和参数信息，使用 load_model = torch.load('model.pth')，在网络较大的时候加载的时间比较长，同时存储空间也比较大；

（2）加载模型参数信息，需要先导入模型的结构，然后通过 model.load_state_dic (torch.load('model_state.pth')) 来导入。

3.2 线性模型

这一节将从机器学习最简单的线性模型入手，看看 PyTorch 如何解决这个问题。

3.2.1 问题介绍

说起线性模型，大家对它都很熟悉了，通俗来讲就是给定很多个数据点，希望能够找到一个函数来拟合这些数据点使其误差最小，比如最简单的一元线性模型就可以用图3.3来表示。

图 3.3 一元线性模型

图3.3给出了一系列的点，找一条直线，使得直线尽可能与这些点接近，也就是这些点到直线的距离之和尽可能小。用数学语言来严格表达，即给定由 d 个属性描述的示例 x = (x1, x2, x3, • • • , xd)，其中 xi 表示 x 在第 i 个属性上面的取值，线性模型就是试图学习一个通过属性的线性组合来进行预测的函数，即

f (x) = w1x1 + w2x2 + • • • + wdxd + b (3.2)

一般可以用向量的形式来表达：

f (x) = wT x + b (3.3)

其中 w = (w1, w2, • • • , wd)，w 和 b 都是需要学习的参数，模型通过不断地调整 w 和 b，最后就能够得到一个最优的模型。

线性模型形式简单、易于建模，却孕育着机器学习领域中重要的基本思想，同时线性模型还具有特别好的解释性，因为权重的大小就直接可以表示这个属性的重要程度。首先我们从最简单的一维线性回归入手。

3.2.2 一维线性回归

给定数据集 D = {(x1, y1), (x2, y2), (x3, y3), • • • , (xm, ym)}，线性回归希望能够优化出一个好的函数 f (x)，使得 f (xi) = wxi + b 能够与 yi 尽可能接近。

如何才能学习到参数 w 和 b 呢？很简单，只需要确定如何衡量 f (x) 与 y 之间的差别，就像之前讲的一样，可以用它们之间的距离差异

来衡量误差，取平方是因为距离有正有负，我们希望能够将它们全部变成正的。这也就是著名的均方误差，要做的事情就是希望能够找到 w∗ 和 b∗，使得

均方误差非常直观，也有着很好的几何意义，对应了常用的欧几里得距离，基于均方误差最小化来进行模型求解的办法也称为“最小二乘法”。

求解办法其实非常简单，如果求这个连续函数的最小值，那么只需要求它的偏导数，让它的偏导数等于 0 来估计它的参数，即：

通过求解式 (3.6) 和式 (3.7)，我们就可以得到 w 和 b 的最优解：

其中

即为 x 的均值。

3.2.3 多维线性回归

更一般的情况是多维线性回归，比如像前文描述的，我们有 d 个属性，试图学得最优的函数 f (x)：

最小，这也称为“多元线性回归”，同样可以用最小二乘法对 w和 b 进行估计，为了方便计算，可以将 w 和 d 写进同一个矩阵，将数据集 D 表示成一个 m × (d + 1) 的矩阵 X，每行前面 d 个元素表示 d 个属性值，最后一个元素设为 1，即

将目标 y 也写乘向量的形式 y = (y1, y2, • • • , ym)，那么我们就能够得到：

同样对其求导，令它等于 0。

因为上面涉及了矩阵的逆运算，所以需要 XT X 是一个满秩矩阵或者正定矩阵，那么我们可以得到：

所以线性回归模型可以写成：

然而在现实任务中，XT X 往往不是满秩矩阵，就算是满秩矩阵，求解逆的过程也比较慢，所以我们一般可以使用梯度下降法去求解这个最小二乘问题。

3.2.4 一维线性回归的代码实现

讲了这么多原理，下面用 PyTorch 来求解一下一维线性回归问题。

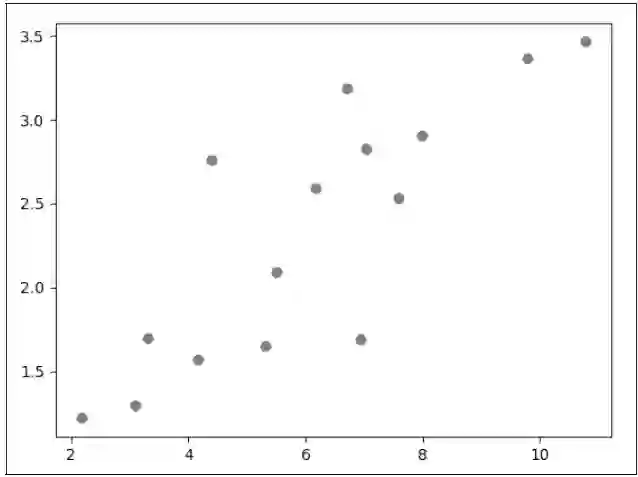
首先我们随便给出一些点：

x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],

[9.779], [6.182], [7.59], [2.167], [7.042],

[10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],

[3.366], [2.596], [2.53], [1.221], [2.827],

[3.465], [1.65], [2.904], [1.3]], dtype=np.float32)

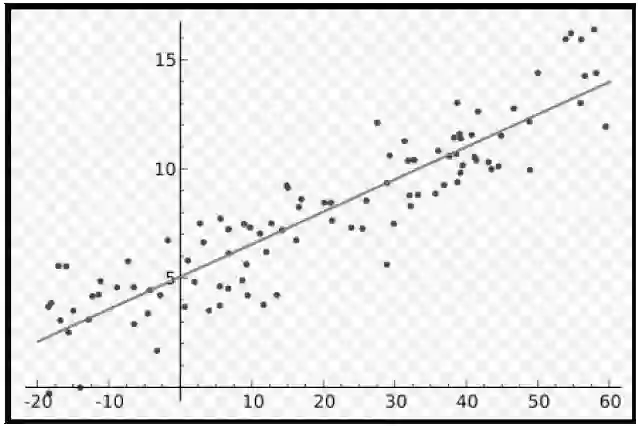
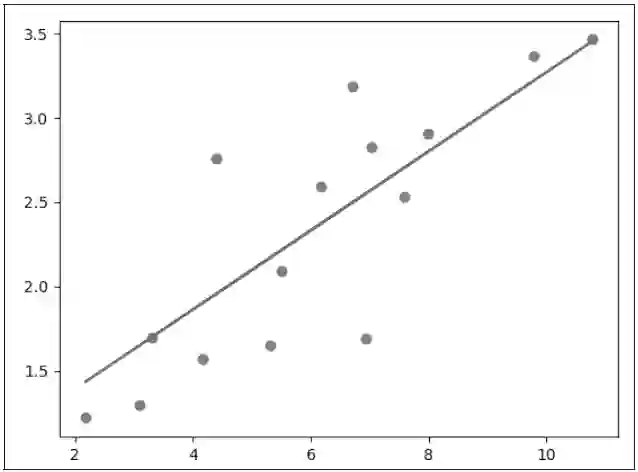
通过 matplotlib 画出来就是这个样子，如图3.4所示。

我们想要做的事情就是找一条直线去逼近这些点，也就是希望这条直线离这些点的距离之和最小，先将 numpy.array 转换成 Tensor，因为 PyTorch 里面的处理单元是Tensor，按上一章讲的方法，这就特别简单了：

x_train = torch.from_numpy(x_train)

y_train = torch.from_numpy(y_train)

接着需要建立模型，根据上一节 PyTorch 的基础知识，这样来定义一个简单的模型：

class LinearRegression(nn.Module):

def __init__(self):

super(LinearRegression, self).__init__()

self.linear = nn.Linear(1, 1) # input and output is 1 dimension

def forward(self, x):

out = self.linear(x)

return out

if torch.cuda.is_available():

model = LinearRegression().cuda()

else:

model = LinearRegression()

图 3.4 matplotlib 画出的图

这里我们就定义了一个超级简单的模型 y = wx + b，输入参数是一维，输出参数也是一维，这就是一条直线，当然这里可以根据你想要的输入输出维度进行更改，我们希望去优化参数 w 和 b 能够使得这条直线尽可能接近这些点，如果支持 GPU 加速，可以通过 model.cuda() 将模型放到 GPU 上。然后定义损失函数和优化函数，这里使用均方误差作为优化函数，使用梯度下降进行优化：

criterion = nn.MSELoss()

optimizer = optim.SGD(model.parameters(), lr=1e-3)

接着就可以开始训练我们的模型了：

num_epochs = 1000

for epoch in range(num_epochs):

if torch.cuda.is_available():

inputs = Variable(x_train).cuda()

target = Variable(y_train).cuda()

else:

inputs = Variable(x_train)

target = Variable(y_train)

# forward

out = model(inputs)

loss = criterion(out, target)

# backward

optimizer.zero_grad()

loss.backward()

optimizer.step()

if (epoch+1) % 20 == 0:

print('Epoch[{}/{}], loss: {:.6f}'

.format(epoch+1, num_epochs, loss.data[0]))

定义好我们要跑的 epoch 个数，然后将数据变成 Variable 放入计算图，然后通过 out=model(inputs) 得到网络前向传播得到的结果，通过 loss=criterion(out,target) 得到损失函数，然后归零梯度，做反向传播和更新参数，特别要注意的是，每次做反向传播之前都要归零梯度，optimizer.zero_grad()。不然梯度会累加在一起，造成结果不收敛。在训练的过程中隔一段时间就将损失函数的值打印出来看看，确保我们的模型误差越来越小。注意 loss.data[0]，首先 loss 是一个 Variable，所以通过loss.data 可以取出一个 Tensor，再通过 loss.data[0] 得到一个 int 或者 float 类型的数据，这样我们才能够打印出相应的数据。

做完训练之后可以预测一下结果。

model.eval()

predict = model(Variable(x_train))

predict = predict.data.numpy()

plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label='Original data')

plt.plot(x_train.numpy(), predict, label='Fitting Line')

plt.show()

首先需要通过 model.eval() 将模型变成测试模式，这是因为有一些层操作，比

如 Dropout 和 BatchNormalization 在训练和测试的时候是不一样的，所以我们需要通过这样一个操作来转换这些不一样的层操作。然后将测试数据放入网络做前向传播得到结果，最后画出的结果如图 3.5所示。

图 3.5 一元回归

这样我们就通过 PyTorch 解决了一个简单的一元回归问题，得到了一条直线去尽可能逼近这些离散的点。

3.2.5 多项式回归

对于一般的线性回归，由于该函数拟合出来的是一条直线，所以精度欠佳，我们可以考虑多项式回归，也就是提高每个属性的次数，而不再是只使用一次去回归目标函数。原理和之前的线性回归是一样的，只不过这里用的是高次多项式而不是简单的一次线性多项式。首先给出我们想要拟合的方程：

y = 0.9 + 0.5 × x + 3 × x2 + 2.4 × x3

然后可以设置参数方程：

y = b + w1 × x + w2 × x2 + w3 × x3

我们希望每一个参数都能够学习到和真实参数很接近的结果。下面来看看如何用 PyTorch 实现这个简单的任务。

首先需要预处理数据，也就是需要将数据变成一个矩阵的形式：

在 PyTorch 里面使用 torch.cat() 函数来实现 Tensor 的拼接：

def make_features(x):

"""Builds features i.e. a matrix with columns [x, x^2, x^3]."""

x = x.unsqueeze(1)

return torch.cat([x ** i for i in range(1, 4)], 1)

对于输入的 n 个数据，我们将其扩展成上面矩阵所示的样子。

然后定义好真实的函数：

W_target = torch.FloatTensor([0.5, 3, 2.4]).unsqueeze(1)

b_target = torch.FloatTensor([0.9])

def f(x):

"""Approximated function."""

return x.mm(W_target) + b_target[0]

这里的权重已经定义好了，unsqueeze(1) 是将原来的 tensor 大小由 3 变成 (3, 1)，x.mm(W_target) 表示做矩阵乘法，f (x) 就是每次输入一个 x 得到一个 y 的真实函数。在进行训练的时候我们需要采样一些点，可以随机生成一些数来得到每次的训练集：

def get_batch(batch_size=32):

"""Builds a batch i.e. (x, f(x)) pair."""

random = torch.randn(batch_size)

x = make_features(random)

y = f(x)

if torch.cuda.is_available():

return Variable(x).cuda(), Variable(y).cuda()

else:

return Variable(x), Variable(y)

通过上面这个函数我们每次取 batch_size 这么多个数据点，然后将其转换成矩阵的形式，再把这个值通过函数之后的结果也返回作为真实的目标。然后可以定义多项式模型：

# Define model

class poly_model(nn.Module):

def __init__(self):

super(poly_model, self).__init__()

self.poly = nn.Linear(3, 1)

def forward(self, x):

out = self.poly(x)

return out

if torch.cuda.is_available():

model = poly_model().cuda()

else:

model = poly_model()

这里的模型输入是 3 维，输出是 1 维，跟之前定义的线性模型只有很小的差别。然后我们定义损失函数和优化器：

criterion = nn.MSELoss()

optimizer = optim.SGD(model.parameters(), lr=1e-3)

同样使用均方误差来衡量模型的好坏，使用随机梯度下降来优化模型，然后开始训练模型：

epoch = 0

while True:

# Get data

batch_x, batch_y = get_batch()

# Forward pass

output = model(batch_x)

loss = criterion(output, batch_y)

print_loss = loss.data[0]

# Reset gradients

optimizer.zero_grad()

# Backward pass

loss.backward()

# update parameters

optimizer.step()

epoch += 1

if print_loss < 1e-3:

break

这里我们希望模型能够不断地优化，直到实现我们设立的条件，取出的 32 个点的均方误差能够小于 0.001。运行程序可以得到如图3.6所示的结果。

图 3.6 程序运行结果

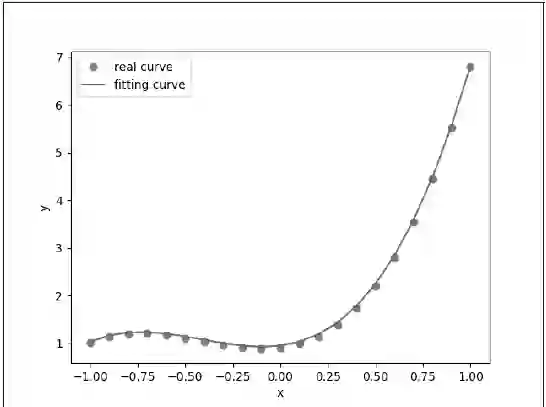
将真实函数的数据点和拟合的多项式画在同一张图上，我们可以得到如图3.7所示的结果。

图 3.7 多项式回归

从两个结果来看，我们已经很接近真实的函数了。现实世界中很多问题都不是简单的线性回归，涉及很多复杂的非线性模型，而线性模型是机器学习中最重要的模型之一，它的统计思想及其非常直观的解释性仍然可以给我们一些启发。

3.3 分类问题

下面这节我们将开始介绍机器学习领域里面的另一个问题：分类问题。

3.3.1 问题介绍

机器学习中的监督学习主要分为回归问题和分类问题，我们之前已经讲过回归问题了，它希望预测的结果是连续的，那么分类问题所预测的结果就是离散的类别。这时输入变量可以是离散的，也可以是连续的，而监督学习从数据中学习一个分类模型或者分类决策函数，它被称为分类器（classifier）。分类器对新的输入进行输出预测，这个过程即称为分类（classification）。例如，判断邮件是否为垃圾邮件，医生判断病人是否生病，或者预测明天天气是否下雨等。同时分类问题中包括有二分类和多分类问题，我们下面先讲一下最著名的二分类算法——Logistic 回归。首先从 Logistic 回归的起源说起。

3.3.2 Logistic 起源

Logistic 起源于对人口数量增长情况的研究，后来又被应用到了对于微生物生长情况的研究，以及解决经济学相关的问题，现在作为回归分析的一个分支来处理分类问题，先从 Logistic 分布入手，再由 Logistic 分布推出 Logistic 回归。

3.3.3 Logistic 分布

设 X 是连续的随机变量，服从 Logistic 分布是指 X 的积累分布函数和密度函数如下：

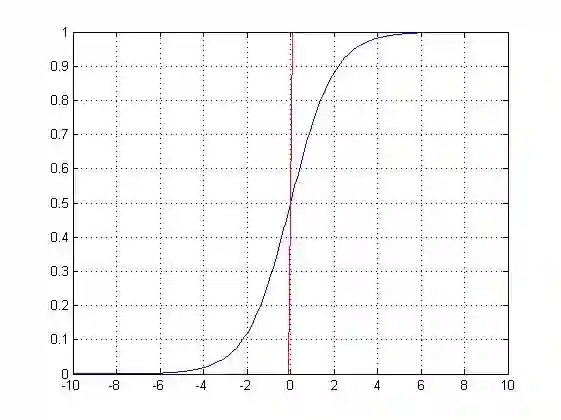
其中 µ 影响中心对称点的位置，γ 越小中心点附近的增长速度越快。下一节会讲到在深度学习中常用的一个非线性变换 Sigmoid 函数是 Logistic 分布函数中 γ = 1, µ = 0 的特殊形式。

(sigmoid)Logistic 函数的表达形式如下：

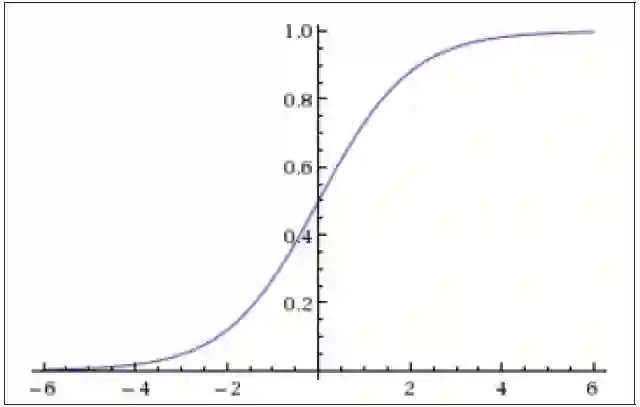
其函数图像如图 3.8所示，由于函数很像“S”形，所以该函数又叫 Sigmoid 函数。

图 3.8 Sigmoid 函数图像

3.3.4 二分类的 Logistic 回归

Logistic 回归不仅可以解决二分类问题，也可以解决多分类问题，但是二分类问题最为常见同时也具有良好的解释性。对于二分类问题，Logistic 回归的目标是希望找到一个区分度足够好的决策边界，能够将两类很好地分开。

假设输入的数据的特征向量 x ∈ Rn，那么决策边界可以表示为 ∑ni=1 wixi + b = 0；假设存在一个样本点使得 hw(x) = ∑ni=1 wixi + b > 0，那么可以判定它的类别是 1；如果 hw(x) = ∑mi=1 wixi + b < 0，那么可以判定其类别是 0。这个过程其实是一个感知机的过程，通过决策函数的符号来判断其属于哪一类。而 Logistic 回归要更进一步，通过找到分类概率 P (Y = 1) 与输入变量 x 的直接关系，然后通过比较概率值来判断类别，简单来说就是通过计算下面两个概率分布：

其中 w 是权重，b 是偏置。现在介绍 Logistic 模型的特点，先引入一个概念：一个事件发生的几率（odds）是指该事件发生的概率与不发生的概率的比值，比如一个事件发生的概率是 p，那么该事件发生的几率是

对于 Logistic 回归而言，我们由式（3.16）和式（3.17）可以得到：

这也就是说在 Logistic 回归模型中，输出 Y = 1 的对数几率是输入 x 的线性函数，这也就是 Logistic 回归名称的原因。如果观察式（3.17），则可以得到另外一种 Logistic 回归的定义，即线性函数的值越接近正无穷，概率值就越接近 1；线性函数的值越接近负无穷，概率值越接近 0。因此 Logistic 回归的思路是先拟合决策边界（这里的决策边界不局限于线性，还可以是多项式），在建立这个边界和分类概率的关系，从而得到二分类情况下的概率。

3.3.5 模型的参数估计

上面我们简单地介绍了 Logistic 回归模型的建立，下面通过极大似然估计来求出模型中的参数。对于给定的训练集数据 T = {(x1, y1), (x2, y2), • • • (xn, yn)}，其中 xi ∈ Rn, yi ∈{0, 1}，假设 P (Y = 1|x) = π(x)，那么 P (Y = 0|x) = 1 − π(x)，所以似然函数可以有如下的表达：

对 L(w) 求极大值就能够得到 w 的估计值，可以使用最简单的梯度下降法来求得。用 L(w) 对 W 求导，可以得到：

求出梯度之后就可以使用迭代的梯度下降来求解。

3.3.6 Logistic 回归的代码实现

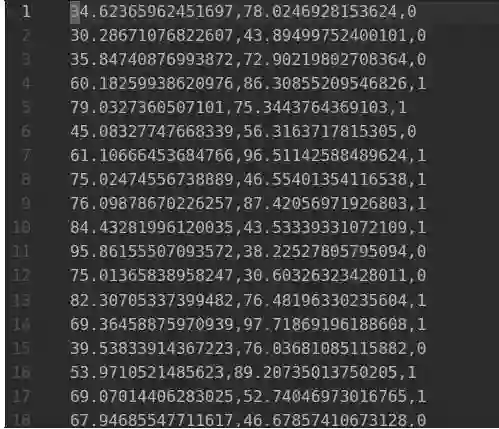
首先我们打开 txt 文件，可以看到数据存放的方式，如图3.9所示。

图 3.9 数据存放

每个数据点是一行，每一行中前面两个数据表示 x 坐标和 y 坐标，最后一个数据表示其类别。我们先从 data.txt 文件中读取数据，使用非常简单的 python 读取 txt 的方法就能够实现。

with open('data.txt', 'r') as f:

data_list = f.readlines()

data_list = [i.split('\n')[0] for i in data_list]

data_list = [i.split(',') for i in data_list]

data = [(float(i[0]), float(i[1]), float(i[2])) for i in data_list]

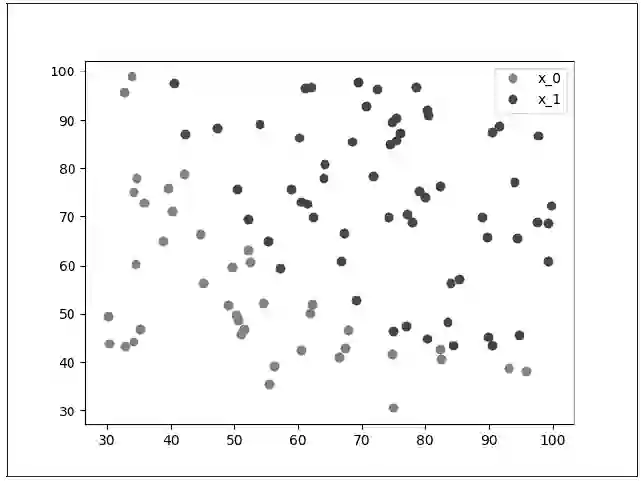
然后通过 matplotlib 能够简单地将数据画出来。

x0 = list(filter(lambda x: x[-1] == 0.0, data))

x1 = list(filter(lambda x: x[-1] == 1.0, data))

plot_x0_0 = [i[0] for i in x0]

plot_x0_1 = [i[1] for i in x0]

plot_x1_0 = [i[0] for i in x1]

plot_x1_1 = [i[1] for i in x1]

plt.plot(plot_x0_0, plot_x0_1, 'ro', label='x_0')

plt.plot(plot_x1_0, plot_x1_1, 'bo', label='x_1')

plt.legend(loc='best')

首先将两个类别分开，然后将所有的数据点画出就能够得到图3.10。

图 3.10 数据点

从图3.10中我们可以明显看出这些数据点被分为两个类：一类用红色的点，一类用蓝色的点，我们希望通过 Logistic 回归将它们分开。接下来定义 Logistic 回归的模型，以及二分类问题的损失函数和优化方法。

class LogisticRegression(nn.Module):

def __init__(self):

super(LogisticRegression, self).__init__()

self.lr = nn.Linear(2, 1)

self.sm = nn.Sigmoid()

def forward(self, x):

x = self.lr(x)

x = self.sm(x)

return x

logistic_model = LogisticRegression()

if torch.cuda.is_available():

logistic_model.cuda()

criterion = nn.BCELoss()

optimizer = torch.optim.SGD(logistic_model.parameters(), lr=1e-3,

momentum=0.9)

这里 nn.BCELoss 是二分类的损失函数，torch.optim.SGD 是随机梯度下降优化函数。然后训练模型，并且间隔一定的迭代次数输出结果。

for epoch in range(50000):

if torch.cuda.is_available():

x = Variable(x_data).cuda()

y = Variable(y_data).cuda()

else:

x = Variable(x_data)

y = Variable(y_data)

# ==================forward==================

out = logistic_model(x)

loss = criterion(out, y)

print_loss = loss.data[0]

mask = out.ge(0.5).float()

correct = (mask == y).sum()

acc = correct.data[0] / x.size(0)

# ===================backward=================

optimizer.zero_grad()

loss.backward()

optimizer.step()

if (epoch+1) % 1000 == 0:

print('*'*10)

print('epoch {}'.format(epoch+1))

print('loss is {:.4f}'.format(print_loss))

print('acc is {:.4f}'.format(acc))

其中 mask=out.ge(0.5).float() 是判断输出结果如果大于 0.5 就等于 1，小于

0.5 就等于 0，通过这个来计算模型分类的准确率。

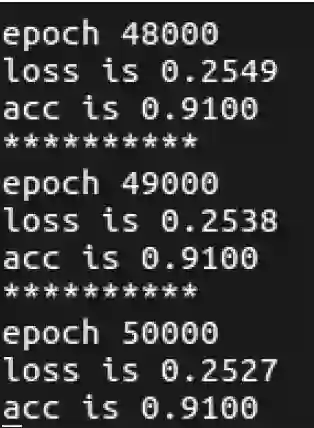
训练完成我们可以得到图 3.11所示的 loss 和准确率。因为数据相对简单，同时我们使用的是也是简单的线性 Logistic 回归，loss 已经降得相对较低，同时也有 91% 的准确率。

图 3.11 loss 和准确率

我们可以将这条直线画出来，因为模型中学习的参数 w1，w2 和 b 其实构成了一条直线 w1x + w2y + b = 0，在直线上方是一类，在直线下方又是一类。我们可以通过下面的方式将模型的参数取出来，并将直线画出来，如图 3.12所示。

w0, w1 = logistic_model.lr.weight[0]

w0 = w0.data[0]

w1 = w1.data[0]

b = logistic_model.lr.bias.data[0]

plot_x = np.arange(30, 100, 0.1)

plot_y = (-w0 * plot_x - b) / w1

plt.plot(plot_x, plot_y)

plt.show()