【学界】Bengio最新论文提出GibbsNet:深度图模型中的迭代性对抗推断
来源:机器之心
Yoshua Bengio 等研究者最近提出了 GibbsNet,该方法可以学习数据和隐编码之间的联合分布,该方法使用对抗学习迭代步骤来逐步提炼联合分布 p(x, z),以更好地在每一步上匹配数据分布。该论文已被 NIPS 2017 大会收录。
生成模型是学习复杂数据隐藏表征的强大工具。早期的无向图模型展现出强大的潜力,如深度玻尔兹曼机或 DBM(Salakhutdinov and Hinton, 2009),但它们实际上并不能很好地适应复杂的高维特征空间(远超 MNIST),这可能是因为模型优化与混合方面的困难(Bengio et al.,2012)。但近来 Helmholtz 机(Bornschein et al., 2015)和变分自编码器(Kingma and Welling, 2013)的研究工作借鉴了深度学习工具,并能实现非常好的效果,这两种方法现在已经在很多领域上得到了采用(Larsen et al., 2015)。
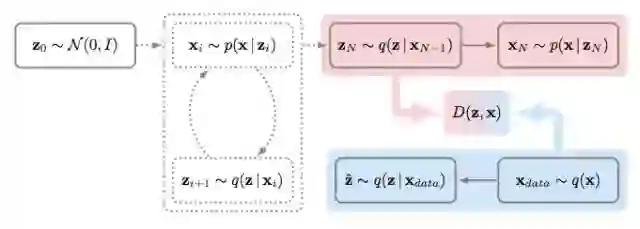
图 1:上图展示了 GibbsNet 的训练过程。unclamped 链(虚线部分)从各向同性高斯分布 N(0, I) 开始迭代 N 个步骤。最后一个迭代步(N)以实线粉框表示,然后使用联合判别器 D 将其与 clamped 链(实线蓝色框)中的单步数据进行比较。
在这篇论文中,Bengio 等研究者表明以上那些非常复杂的有向图模型依赖于近似推断进行训练,但目前有证据表明近似后验在实践中限制了生成器的能力。因此若我们从推断(编码器)和生成过程(解码器)开始,并直接从这些过程推导出先验知识可能更简单。这种作者称之为 GibbsNet 的方法使用这两个过程来定义马尔科夫链相似到 Gibbs 采样的转换运算,并在采样观察值与采样隐变量之间进行交替。
该论文所提出的方法主要有以下重要的贡献:
本论文为深度图模型中的学习和推断等新方法提供了理论基础。该算法得出的模型和无向图模型非常相似,但避免了对基于最大似然估计方法进行训练的需求,也缺少了一个明确定义的能量函数,反而该论文通过使用类似 GAN 判别器的方法进行训练。
本论文还提出了一个在对抗框架中执行推断的稳定方法,这意味着有效推断是在编码器和解码器网络的各种架构下执行的。这种稳定性来源于编码器 q(z | x) 同时出现在 clamped 和 unclamped 链中,因此我们可以从 clamped 链中的判别器和 unclamped 中的梯度获得训练信号。
本论文还展示了使用简单先验 p(z) 在模型隐藏空间中的质量提升,这体现在提升的条件生成中。隐藏空间的表现力也体现在运行成块 Gibbs 采样时会产生更平滑的混合,体现在推断隐藏空间中的类别会有更好的分离。
本论文的模型具有无向图模型的灵活性,包括在非特性训练的单个模型中所表现出来的标注预测能力、条件类别生成能力和联合图像-标注生成能力等。本论文所提出的 GibbsNet 是第一个将这种灵活性与在自然图像上生成高质量样本能力相结合的模型。
论文地址:https://arxiv.org/abs/1712.04120
摘要:将联合分布构建为 p(x, z) = p(z)p(x | z) 的有向隐变量模型的优势为快速、精确的采样。但是,这类模型的缺陷是需要指定 p(z),通常指定为一个简单的固定先验来限制该模型的表达能力。无向隐变量模型不需要将 p(z) 指定为先验值,利用这类模型进行采样通常需要迭代步骤,如需要多步才能从联合分布 p(x, z) 中采样的成块吉布斯采样(blocked Gibbs-sampling)。我们提出一种新方法来学习数据和隐编码之间的联合分布,该方法使用对抗学习迭代步骤来逐步提炼联合分布 p(x, z),以更好地在每一步上匹配数据分布。GibbsNet 在理论和实践中都是最好的模型。它具备有向隐变量模型的速度和简洁性,保证仅使用几次采样迭代实现从 p(x, z) 中采样的过程(假设对抗博弈达到虚拟训练标准全局最小值)。同时还具备无向隐变量模型的表达能力和灵活性,无需指定 p(z) 即可使用单个模型执行属性预测、类别-条件生成和联合图像属性建模任务,且该模型未经这些任务的训练。实验证明,GibbsNet 能够学习更复杂的 p(z),从而实现几十步实现图像修补和 p(x, z) 的迭代提炼,无需数千步即可稳定生成,尽管训练过程只需要几步。
2. 提出方法:GibbsNet
GibbsNet 旨在通过匹配模型期望的联合分布和数据驱动的联合分布直接定义和学习转换算子(transition operator),然后使用转换算子训练图模型。这与无向图模型类似,也受到其启发,期望跃迁算子(对应成块吉布斯采样)沿着已定义能量流形移动,这样我们就可以在公式中建立该连接。
2.2 架构
GibbsNet 通常包括三个网络:推断网络 q(z|x)、生成网络 p(x|z) 和联合判别器。通常,我们的这些网络架构遵循 Dumoulin et al.(2017)提出的架构,希望我们使用的 boundary-seeking GAN(BGAN, Hjelm et al., 2017)能够显著优化对立分布的匹配(该案例中指模型期望的联合分布和数据驱动的联合分布),这允许我们使用离散变量,即用标签或离散属性学习图,这种方法在我们的实验中表现良好。
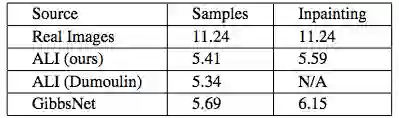
表 1:不同模型的 Inception Score。图像修复结果通过修复图像左半边同时运行四步获取。采样指无条件采样。
图 4:学习转换算子的方法的 CIFAR 样本。1000 步后的非平衡热力学(Sohl-Dickstein et al., 2015)(左),20 步后的 GibbsNet(右)。
图 5:SVHN 的图像修复结果,其中右半边是给定的图像,左半边是修复的结果。
☞ 【最详尽的GAN介绍】王飞跃等:生成式对抗网络 GAN 的研究进展与展望
☞ 【智能自动化学科前沿讲习班第1期】王飞跃教授:生成式对抗网络GAN的研究进展与展望
☞ 【智能自动化学科前沿讲习班第1期】王坤峰副研究员:GAN与平行视觉
☞ 【重磅】平行将成为一种常态:从SimGAN获得CVPR 2017最佳论文奖说起
☞ 【“强化学习之父”萨顿】预测学习马上要火,AI将帮我们理解人类意识
☞ 【TFGAN】谷歌开源 TFGAN,让训练和评估 GAN 变得更加简单
☞ 【NIPS 2017】清华大学人工智能创新团队在AI对抗性攻防竞赛中获得冠军
☞ 【英伟达NIPS论文AI脑洞大开】用GAN让晴天下大雨,小猫变狮子,黑夜转白天