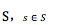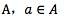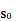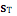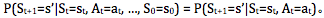伯克利 AI 课程:深度强化学习之马尔科夫决策过程(视频)
新智元推荐
来源:微信AI
作者:叶浩
【新智元导读】文章内容是通过学习伯克利的 AI 课程后转写的,有讲的不明白的地方,可以去看一下原始课程的视频,8-11课。
强化学习简短概括:通过观察机器人在与外界系统的决策交互过程中,产生的状态变化以及带来的收益,学习一个最优的决策模型,使得未来进行自动决策的时候能获得期望最大化的累积收益。
这里有两个很重要的概念在后面的文章中反复提到,也是要解决的问题,需要牢记。一个是累积收益,不能只看眼前的一步决策,简单粗暴的用贪心策略。同时要考虑交互过程状态转移的不确定性,目标是求解累积收益的期望最大化,而不能简单理解为能用if else表达的动态规划。
为了能更好的理解深度强化学习,我们需要从最开始的马尔科夫决策过程开始,逐步深入,最后才能明白为什么我们需要用深度神经网络结合强化学习,以及这样做解决了什么问题。文章内容是通过学习伯克利的 AI 课程后转写的,有讲的不明白的地方,可以去看一下原始课程的视频,8-11课。
最后一篇后,我们可以用 DQN 开发一个学习机器,自动玩 flappy bird 。效果如下:
下面开始第一部分。
不确定性主要是用来描述现实生活中的一些环境因素对你做出的决策的响应是不确定的。他并不像我们写的程序严格的按照 if else 的分支来走,而是事件响应的结果包含一些受环境影响的随机性因素。搜索在这里是一个大的概念,不是我们说的狭义的“搜索引擎”。它是面向一个目标进行(搜索)路径的规划,可以理解为像搜索树一样的寻找目标。
两者结合,不确定的搜索问题,可以简单理解为在按照某种方式进行(搜索)寻路的过程中,存在不确定性,并不是严格意义上的不是向左就是向右子树转移的过程。
一个简单的例子,让机器人沿着峭壁走去取宝石,向左走向右走,也可以向前走,如果看成是一个取宝石的路径搜索问题,从一个点出发,有左右前三个子树可以转移,到达下一个状态后,又可以左右前。但是在真实环境中,这个问题是含有不确定性的。即使发出的动作是向右走,会不会有一定概率掉到火坑里面(局面实际上转变成了向前走),都是可能的。这种不确定性,我们可以观察学习到,但是发生的过程完全不受我们控制。
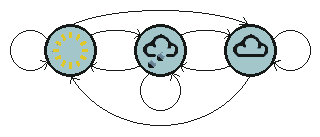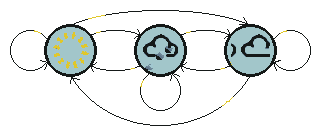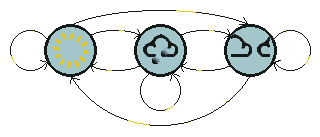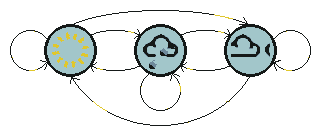
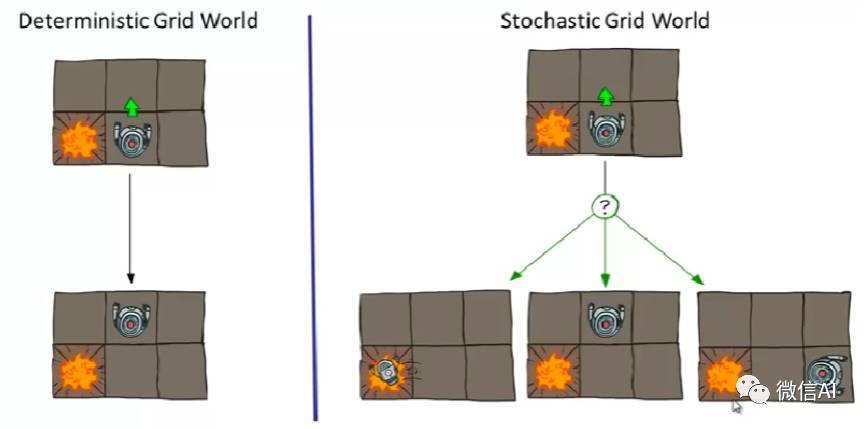
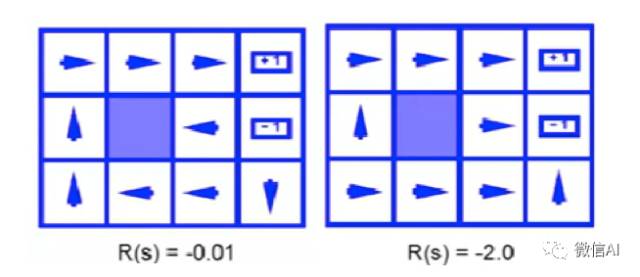
确定性和随机性可以用下面一个图简单的表示(此时请抛开程序员 if else hard code的思维)。左图是理想情况,系统作出的决策是向上走,永远只有一个结果就是机器人向上挪动;右图更贴近于真实环境,系统作出的决策是向上走,但是在一个具有不确定性的环境下,最后的响应会是机器人往哪个方向挪动,是具有一定随机性的,随机性的分布,这个取决于环境。举个例子,真实环境下路面可能打滑,你希望向上走,脚滑了一下就掉左边坑里面了,😊
在这种具有不确定性的环境中,一般我们都会设定一个目标(比如赢或者输),在向目标前进去做决策路径搜索的时候,我们希望过程中的累积收益最大化。
比如以上面机器人自动学习走迷宫的游戏为例,游戏的目标就是找到宝石,并且避免掉入火坑。我们可以把目标达成(获得宝石或者掉进火坑)设定为结束态,机器人在这两个状态下会得到一个大额的奖励或者惩罚。只要没到结束态,每走一步,都会得到一个当前存活的奖励。当然,这个存活奖励也可以为负数,比如你始终在里面打转刷分,或者一直拖着不达成目标(结束游戏)是不可行的。
我们希望有一个模型能自动学会如何玩这个游戏(描述如何对状态和动作路径进行搜索,解决一个问题),最后的目标是,到达结束态后,使得所有奖励累加和最大化。
上述不确定性问题可以用马尔科夫决策过程来描述。我们先给出一些马尔科夫决策过程的符号定义:
a. 一个状态(state)s的集合
b. 一个动作(action)a的集合
c. 一个转换函数 T(s, a, s’),简单理解为条件概率 P(s’|s, a)
d. 一个奖励(reward)函数R(s, a, s’),这包含中间激励和最后结束态的大奖励
e. 给定一个初始状态,有的教材标记为
f.(可能需要)给定一个结束状态,有的教材记序列长度为T,结束态标记为
MDP是一类不确定性的搜索问题,我们的目标是结合奖励函数搜索一个可行的状态转换路径(state 和 action 的序列)使得奖励最大化。
至于为什么叫马尔科夫决策过程呢?那是因为认为状态转换,只跟当前时刻的 state 和 action 有关:
决策体现在你要根据 state 和潜在的奖励,选择一个 action ;不确定性体现在转换函数,状态 s 下执行动作 a ,最后到达的状态 s’ 具有不确定性,奖励 R 同理。
在一个确定性的单agent搜索问题中,我们搜索的目标,是一个从起始状态到结束态的最优的路径规划,或者一个 action 的序列。但是在 MDP 中,由于不确定性的存在,我们无法得到一个严格的序列,我们只能得到一个最优的决策函数,由它告诉我们每一步应该怎么走,我们称之为策略(policy),标记为 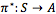
把上面的游戏数字化,可以发现当奖励函数不一样的时候,最优策略是不一样的。注意火坑(reward=-1)左边的 state ,如果每一步得到的 reward 是 -0.01,最优策略是向左走,这样有一定概率进入上面和下面的状态,而多次尝试的累计 reward 负数并不会太大;相反,如果单步 reward 被设置成 -2.0,这个状态的最佳策略是直接跳进火坑,死了也就是-1.0,比其他任何 action 得到的收益都要大。
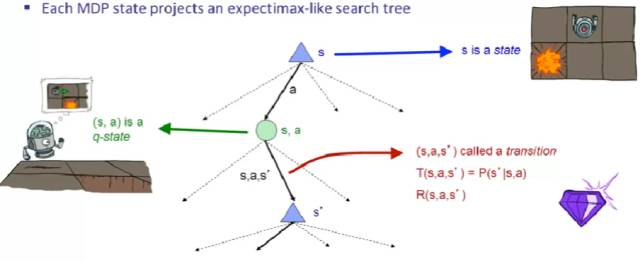
为了方便理解 MDP,我们把 MDP 的状态转移展开,然后整个求期望奖励最大化的过程,可以看做是一个期望最大化的搜索树里面的搜索过程(需要时刻牢记不确定性)。
解释一下下面的图,他引入了一个很重要的概念:q-state。我们在一个状态s,follow 策略选择了动作 a,这里需要引入一个中间态的树节点 (s,a) ,称之为 q-state 。这个节点的意思是,(s,a) 完成了决策过程,但是状态转换并没有完成,因为 (s,a) 得到的是哪个 s’,这里面还具有一些不确定性,也就是 P(s’|s,a) 的存在。q-state 还需要经过一个 transition 才最后输出 s’,同时得到奖励 R(s,a, s’)。
上面说到了我们的策略需要得到的是从开始到结束态的期望奖励累计总和最大化,那么就会面临一个问题:每一次状态转换都会得到或大或小的 reward ,显然我们要兼顾考虑当前转换的 reward ,同时也要考虑此次转换对后续的影响以及后续能获得的 reward 。那么最优策略在进行路径搜索的时候,是优先抓住当前 reward ,还是优先考虑积攒到后面再一次性变现?当不同时期的 reward 大小出现明显差异时,谁都知道要取大的。但是当 reward 大小并没有明显差异时,是先苦后甜还是先甜后苦,如何决策呢?
结合我们的最终目标,是最大化奖励的总和。那么更合理的策略,是把当前能获得的奖励都拿到手。除非未来的奖励能出现暴涨性的升值,否则相同价值的东西放在以后兑现,总是没有现在直接拿到手里值钱的。
由此就引出了奖励的折扣问题,我们站在当前 timestep ,去计算未来的综合收益时,需要对未来的奖励进行打折,打折系数记为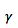
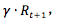
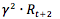
打折除了是考虑价值贬值,也有利于算法收敛。因为到达结束态的决策过程可能是非常长,甚至是一个无限的状态转换序列(比如 flappybird ),我们也不可能无限期的计算,去考虑未来的收益。引入折扣系数后,基本可以忽略未来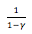
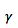
当然,除了引入折扣系数的方法,还有其他方法来处理无限序列问题,这里就不展开讲了。可以看伯克利 AI 课程的视频。
所有图片版权来自于伯克利教程,或者网络。如有版权冲突请联系我们和微信AI。
课程链接:http://ai.berkeley.edu/home.html
(本文由微信AI 授权转载,特此感谢! )
3月27日,新智元开源·生态AI技术峰会暨新智元2017创业大赛颁奖盛典隆重召开,包括“BAT”在内的中国主流 AI 公司、600多名行业精英齐聚,共同为2017中国人工智能的发展画上了浓墨重彩的一笔。
点击阅读原文,查阅文字版大会实录
访问以下链接,回顾大会盛况: