线性代数的直观指南 第三部分

翻译小组成员介绍: 胡智杰    

 谢菲尔德大学 数学与统计学硕士(在读)

英文网址: betterexplained.com/articles/linear-algebra-guide/

解联立方程

Solving Simultaneous equations

数字表(还不是“矩阵”)的早期使用是为线性系统记账:

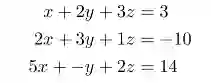
就变成了

我们可以通过在矩阵和输出中添加/减去行来避免重写完整的方程组。当矩阵演变成单位矩阵时，输出端显示x、y和z的值。

这个过程叫做高斯-若尔当消元法，它可以节省计算的时间。然而，线性代数主要是关于矩阵变换的，而不是求解大型方程组。

术语，行列式，特征元

Terminology, Determinants, And Eigenstuff

词汇有专门的类别来描述它们的用法(名词、动词、形容词)。矩阵同样可以细分。请看这里《图解线性代数》系列文章. 

像“上三角”、“对称”、“对角线”这样的描述是矩阵的形状，并影响它们的变换。

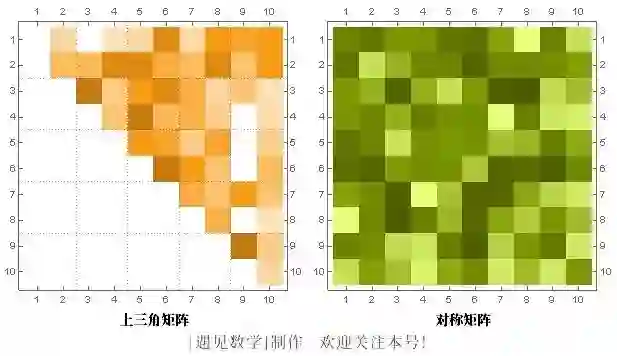
可视化矩阵

行列式是输出变换的“大小”。如果输入是单位向量(表示面积或体积为1)，行列式就是变换后的面积或体积的大小。行列式为0意味着矩阵是“破坏性的”且不可逆转(类似于乘以零:信息丢失)。

特征向量和特征值表示变换的“轴”。比如想想旋转一个地球仪:除了两极, 每个地方都有一个新的方向。

“特征向量”是一个输入，当它通过矩阵时不会改变方向(它指向“沿轴”)。虽然方向没有改变，但大小可能会改变。特征值是特征向量在经过矩阵时放大或缩小的量。

矩阵作为输入项

Matrices As Inputs

首先有一个奇怪的想法: 我们可以把运算操作矩阵也当作输入项!

操作矩阵类似于: 要修改的命令。将一个操作矩阵应用到另一个操作矩阵中，会得到一个新的操作矩阵，按照顺序应用这两个转换。

如果 N 是“为股市新闻调整投资组合”，T 是“为税改政策调整投资组合”，则两者均适用:

TN = X

表示“创建矩阵X，它首先根据股市新闻进行调整，然后根据税改政策进行调整”。哇!我们不需要输入投资组合，我们直接将一个矩阵再应用到另一个矩阵上。

线性代数的美妙之处在于用一个字母表示整个电子表格的计算。想要多次应用相同的转换吗? 使用 N²或 N³. 这样矩阵的幂就好了。

最后

Onward

我忽略了一些线性代数的细节地方，并且我可以这样。为什么?

这些比喻帮助我用矩阵来思考问题，而不是用我侥幸通过的数学课程来思考问题。我终于可以回答“为什么线性代数有用?”, “为什么电子表格有用?”

它们不是，除非你想要一个工具来解决几乎所有现实世界的问题。问问商人，他们是愿意捐肾，还是永远被Excel禁止。这就是我们所忽略的线性代数的影响: 将电子表格引入数学方程的高效表示法。

快乐学数学!