弱等效原理的多信使检验｜引力波天文学之六

海归学者发起的公益学术平台

分享信息，整合资源

交流学术，偶尔风月

提起伽利略的比萨斜塔实验，可谓是家喻户晓。知社引力波天文学系列第六篇文章，将带领大家一起领略现代版的“比萨斜塔实验”——引力波时代的爱因斯坦弱等效原理检验。知社特约国内相关领域一线年轻学者撰写引力波天文学之系列刊发，以飨读者。

特别声明：本系列科普文章都是相关学者基于他们将要申请、正在执行、或者已经结题的国家自然科学基金委支持的《国家自然科学基金项目》发展出来的，版权归作者所有。

恰逢爱因斯坦广义相对论问世100周年之际，LIGO科学合作组织于2015年9月14日第一次直接探测到了广义相对论预言的引力波信号GW150914，自此人类正式打开了引力波研究宇宙的新窗口。这一成果具有划时代的意义，必将对整个天文学领域乃至基础物理学领域带来革命性的影响。全世界的物理学家和天文学家已经开始利用这一全新的信使——引力波来研究宇宙。正如《知社学术圈》之引力波天文学系列文章的第一篇中（诺奖后的下轮豪赌: 寻觅LIGO引力波源的电磁对应体? | 引力波天文学之一）所说的，引力波天文学当前最重要的问题是寻找引力波源的电磁对应体，确定引力波的天体物理起源。在未来的多信使观测时代，借助引力波信号及其电磁对应体信号，人们可以精确检验爱因斯坦广义相对论以及广义相对论和其它引力理论的基石之一——弱等效原理。下面，我们将向大家详细介绍弱等效原理的多信使检验。

何为爱因斯坦等效原理？

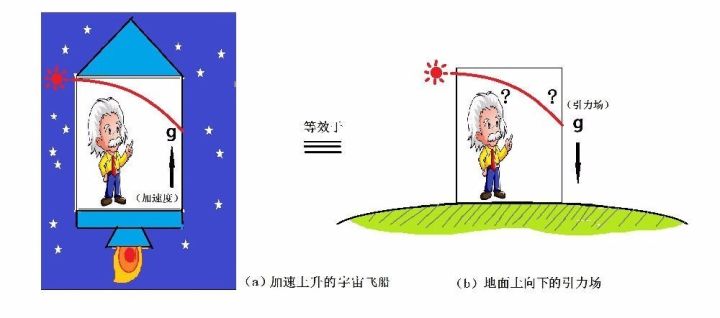
等效原理是爱因斯坦广义相对论和其它引力理论的重要基石，爱因斯坦认为等效原理是他的“happiest idea”（“最开心的灵感”）。爱因斯坦等效原理是一个深远的概念[1]，它的成立需满足三个条件：1、弱等效原理是有效的；2、任何局部非引力实验的结果是不受自由下落无自转参考系速度的影响，即局部洛伦兹不变性；3、在宇宙中任何位置和任何时刻开展的任何局部非引力实验的结果是独立的，即局部位置不变性。其中，条件一弱等效原理的直接描述为：惯性质量=引力质量。举个例子：如图1所示，假设地球上的一个封闭的电梯里有一个人，此时他只受到地球重力的作用，他站在称上的体重为65公斤。如果把这个封闭的电梯放在没有引力场的环境中，并且在电梯底部放一个火箭，火箭推动电梯向上做加速运动，加速度正好等于重力加速度。那么，此时电梯里的人就会感受到和电梯停止在地球表面时完全一样的感觉，他站在称上的体重依旧是65公斤。也就是说，封闭电梯里的人分不清自己是在地球表面静止不动，还是在没有引力场的环境中做加速度运动，地球的局部引力效应与加速度向上运动的效应是可以等效的。这就是弱等效原理的一种表达方式。因此，弱等效原理的抽象表述可以是指局部观测者在局部的区域内由物体所产生的引力可以等效于由加速度所产生的惯性力。虽然条件二和三的定义看起来有点玄乎，但是简单点说，条件二讲的是结果与速度无关，条件三讲的是结果与位置和时间无关，也就是说我们计算的时候不用考虑参考系的速度、位置、时刻。爱因斯坦等效原理实际上是从弱等效原理推广而来的，前面我们提到的弱等效原理都只是针对力学效应，如果将“力学效应”推广到“任何物理效应”，比如“光电效应”，就是爱因斯坦等效原理。本篇文章主要介绍弱等效原理的检验。

 

图1：弱等效原理示意图（图片取自网络）。

自广义相对论问世以来，科学家们发展了各种与爱因斯坦广义相对论不同的引力度规理论。为了区分不同的引力理论，科学家们建立起了一整套叫做后牛顿参数化(parametrized post-Newtonian formalism)的体系来描述不同的引力度规和度规引力势[2]。过程自然是公式连篇，最后的结果也是相当繁杂，包含了10个后牛顿参数。幸运的是，不同的引力理论所预言的后牛顿参数值有些是不一样的。例如，任何符合弱等效原理的引力理论（包括广义相对论），预言不同粒子（包括质量可以忽略的非带电粒子）都会对应相同的后牛顿参数γ值（γ反映了单位质量引起的空间弯曲）；其中广义相对论预言γ值为1。因此人们可以通过测量后牛顿参数的值是否与引力理论的预言一致，从而来检验相应的引力理论是否正确。

“银河系比萨斜塔”实验

根据Shapiro时间延迟效应[3]，一个质量可以忽略的中性粒子（如光子、中微子甚至引力波，其优点是真空中的速度都是相同的常数，即光速c）在引力场中传播会因为引力场的作用而产生时间延迟，即穿越的时间比没有引力场情况要来得长，用公式表达出来就是：，其中γ是后牛顿参数，U(r)是引力势。Shapiro时间延迟正比于引力势沿着粒子传播路径的积分。上面我们提到，任何符合弱等效原理的引力理论（包括广义相对论），预言不同粒子（质量可以忽略的中性粒子）都会对应相同的γ值，即γ1=γ2≡γ，其中下标1、2对应不同的粒子。如果弱等效原理成立的话，不同的粒子在穿越同一引力场后，都会产生相同的Shapiro时间延迟。只要不同的粒子是同时出发的，行走的路径又一样，那么它们就会同时到达地球。而如果弱等效原理不成立的话，不同粒子所对应的γ值就不再相同，因此就会造成不同的粒子产生的Shapiro延迟不一样，进而导致同时出发的粒子到达地球的时间不一样。弱等效原理不成立所引起的时间延迟的表达式为：，其中γ值的差异∆γ=γ1-γ2可以用来表示弱等效原理假设的破缺程度。如果弱等效原理严格成立，则γ值的差异应该严格等于零。

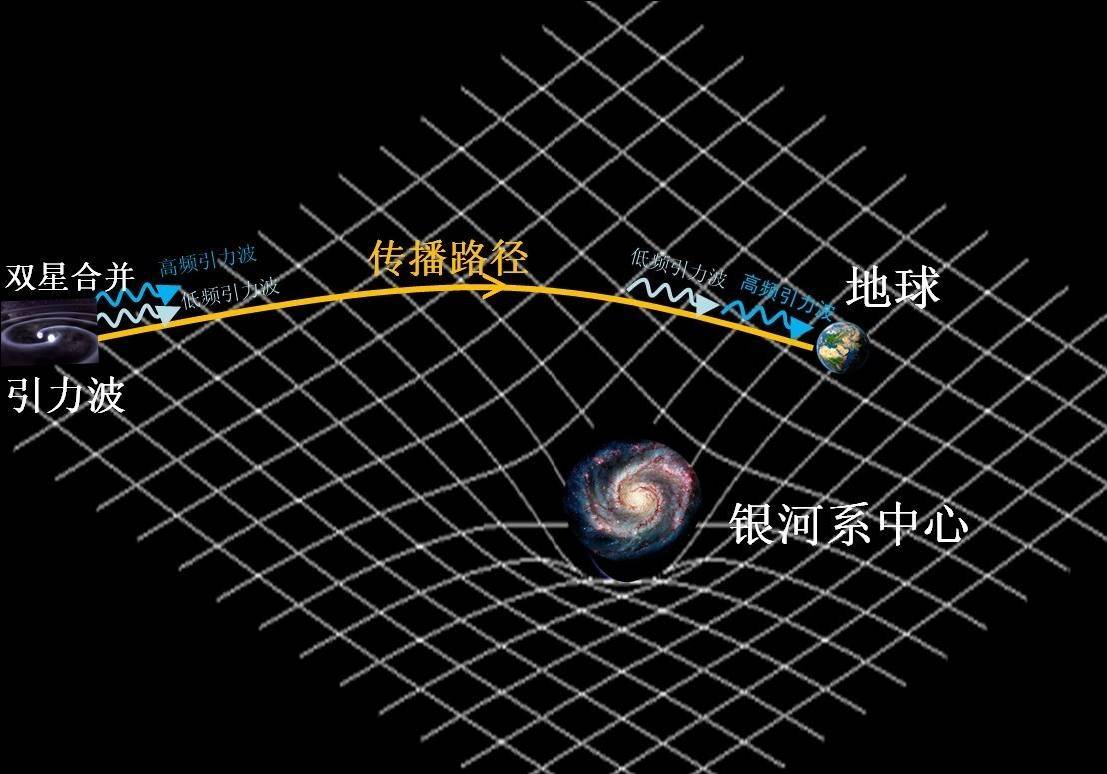
十六世纪，著名物理学家伽利略曾在比萨斜塔上做自由落体实验，如图2所示。他把两个质量不等的球体从塔尖同时扔下，在不考虑空气阻力的前提下，这两个球体会同时落地。该实验表明任何物体，无论其质量大小，在地球引力的作用下具有同样的重力加速度。伽利略的比萨斜塔实验其实就是对弱等效原理的检验，因为弱等效原理预言所有粒子，无论其质量，在引力场中具有同样的加速度。如果我们不再考虑地球的引力势，而是考虑银河系的引力势，那么我们就可以开展“银河系比萨斜塔”实验。对于银河系外的暂现源，不同种类的粒子或不同频率的相同粒子在到达地球之前，必将受到银河系引力场的影响，导致产生相应的Shapiro延迟，如图3所示。因此，弱等效原理可以通过对比河外暂现源同时释放的光子、中微子甚至引力波，或不同频率的同一种粒子（比如光子），在通过同一个引力场所产生的时间差来检验，即比较不同粒子或不同频率的同一种粒子在银河系引力场中传播对应的后牛顿参数γ值的差别是否为零，该检验被形象地称之为“银河系比萨斜塔实验”[4]。

图2：比萨斜塔实验卡通图（图片取自网络）。

图3：若弱等效原理存在破缺，银河系外的引力波源同时发出的不同频率引力波穿越银河系引力场，最后到达地球的时间不同。

1988年，M. J. Longo，L. M. Krauss和S. Tremaine首次利用来自超新星1987A的中微子和光子到达地球的时间差，开展了“银河系比萨斜塔”实验[5,6]。该超新星位于大麦哲伦云中，距离地球约15万光年，其发出的中微子和光子到达地球的时间差约为6个小时。大麦哲伦云是银河系的卫星星系，质量比银河系质量小得多，因此其引力势可以忽略不计。假定银河系的质量集中在银心，并且给定银河系的引力势模型，我们就可以计算出中微子和光子之间相应的Shapiro延迟。假设中微子和光子到达地球的观测时间延迟主要是由于弱等效原理不成立所引起的（即中微子和光子所对应的γ值存在差异引起的），M. J. Longo给出了对中微子和光子之间弱等效原理成立的检验为∆γ≤3.4×10^-3。此外，M. J. Longo还根据超新星1987A释放的能量为40 MeV的中微子和能量为7.5 MeV的中微子到达地球的时间差小于10秒，给出了对不同能量中微子弱等效原理成立的检验为∆γ≤1.6×10^-6，即γ值的差异不超过百万分之一。2015年，高鹤等人[7]利用起源于宇宙学距离的伽玛射线暴产生的不同能量光子到达地球的时间差，证明能量为eV（光学波段）、MeV甚至GeV（伽玛射线）的光子，其对应的后牛顿参数γ值差异小于10-7的量级，该结果比前人用超新星中微子的限制至少提高了一个量级。截止到目前人类通过光学观测，验证了γ绝对值在千分之一精度上与广义相对论预言（γ=1）一致[8]，因此高鹤等人的结果将以上结论在电磁波谱上从光学一直延伸到了GeV伽玛射线能段。魏俊杰等人[9]首次提出，河外或宇宙学起源的快速射电暴也可以被用来精确检验弱等效原理。该工作发现以不同频率的射电光子为检验粒子时，后牛顿参数γ值的差异不超过亿分之一，比之前伽玛射线暴的检验精度至少又提高了1~2个量级，并且把对弱等效原理的检验，从光学波段之上，扩展到了射电波段，从而进一步证明了弱等效原理假设的正确性。此外，魏俊杰等人[10]还利用TeV耀变体（TeV blazars）将弱等效原理的检验，在电磁波谱上推广到了能量更高的TeV能段。

行文至此，细心的读者可能会发现上面介绍的对弱等效原理的检验主要是基于不同能量光子的观测时间延迟，唯一的多信使（光子与中微子）检验是来自超新星1987A的观测。实际上，弱等效原理除了可以通过对比银河系外暂现源同时释放的不同能量的同一种粒子（光子、中微子甚至引力波）在通过同一个引力场所用的时间差来检验，还可以通过对比银河系外暂现源同时释放的不同种类粒子，如光子与中微子、引力波与光子、引力波与中微子两两之间的到达时间差来检验。因此，人们迫切需要借助不同观测渠道获得的不同粒子来检验弱等效原理的精确度，包括引力波。

引力波时代的爱因斯坦弱等效原理检验

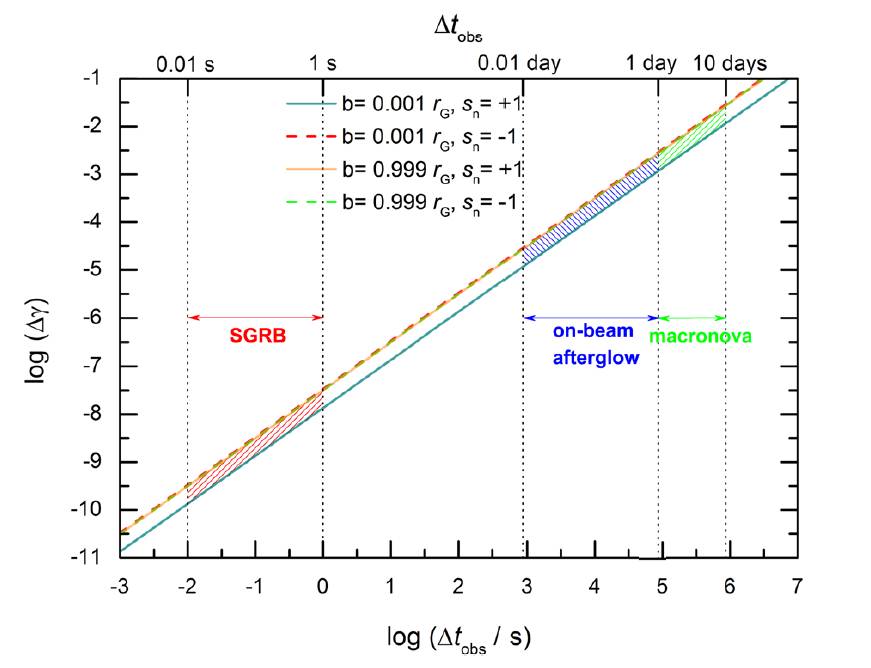
2016年2月11日，LIGO科学合作组织正式向全世界宣布：人类第一次直接探测到了引力波，引力波观测时代已经来临！引力波的成功探测无疑为我们提供了检验弱等效原理新的最佳候选体，因为目前LIGO探测到的四例引力波事件时标都非常短，仅仅毫秒量级，而且都来自银河系外。吴雪峰等人[11]首次利用第一个引力波事件GW150914不同频率引力波信号到达地球的时间差，证明了不同频率引力波信号对应的后牛顿参数γ值差异小于十亿分之一，并且把对弱等效原理的高精度检验扩展到了引力波这个全新的窗口。英国《新科学家》（New Scientist）在2016年2月18日（即LIGO组公布直接探测到引力波的一周后）的Daily News“引力波能揭开的宇宙学四大谜团”把“等效原理”作为引力波能解开的宇宙学四大谜团之一[12]，并在新闻中提到：“中国南京紫金山天文台的吴雪峰说到：‘在GPS和太空航行时代，引力理论预言的哪怕几分钟的误差，都会造成重大后果。它（等效原理）极其重要。’”。考虑升级之后的LIGO/VIRGO的探测能力，吴雪峰等人[11]还指出未来引力波及其电磁对应体信号（极有可能是短时标伽玛射线暴）的联合探测，有望把后牛顿参数γ值的差异限制到约100亿分之一，见图4所示，这一结果比超新星1987A的多信使（光子和中微子）检验结果至少可以提高7个量级。

截止到目前，LIGO和VIRGO已正式公布探测到了四例高置信度的双黑洞并合产生的引力波事件。这些引力波事件的探测触发了全球许多后随观测，试图寻找引力波源的电磁对应体[13]和中微子对应体[14]，但是至今仍未找到任何可靠的对应体。然而，单纯利用引力波信号的观测，人们无法直接认证其天体物理起源，包括深入了解产生引力波信号前后的详细物理过程、发现引力波源的宿主星系、测量宿主星系的红移，因此加快对引力波源的伴随信号，如电磁信号、中微子信号等多信使的探测步伐至关重要。升级之后的LIGO/VIRGO的主要探测目标是双致密天体（双黑洞、双中子星、中子星与黑洞）并合产生的引力波信号，其中学术界讨论最多、认为最有可能实现多信使观测的是双中子星事件[15,16]。那么，LIGO/VIRGO到底能不能探测到双中子星并合产生的引力波事件？让我们翘首以盼吧。

总之，弱等效原理任何可能的破缺都会使人类对自然界基本物理规律的认识更加深刻，所以开展多信使的检验且不断提高其检验精度具有十分重要的科学意义。如果未来真的能够探测到引力波源及其电磁波、中微子伴随信号，那么我们完全能够把对爱因斯坦弱等效原理的多信使检验扩展到引力波和光子、引力波和中微子窗口。

图4：未来引力波信号及其各种电磁信号对弱等效原理（后牛顿参数γ值差异）的可能检验结果。图片取自Wu, X.-F. et al., Physical Review D, 94, 024061 (2016)

作者简介

魏俊杰，中国科学院青年创新促进会会员，2015年于中科院紫金山天文台获得博士学位，2015—2017年任中科院紫金山天文台助理研究员，2017年至今任中科院紫金山天文台副研究员。曾获得2015年度中国科学院院长特别奖、2016年度中国科学院优秀博士学位论文。主要从事观测宇宙学和时域天文研究。

邓灿敏，中国科学院紫金山天文台在读博士生。指导老师：吴雪峰研究员。

参考文献：

[1] Will, C. M. (2014). “The Confrontation between General Relativity and Experiment”. Living Reviews in Relativity, 17, 4

[2] Will, C. M. (2006). “The Confrontation between General Relativity and Experiment”. Living Reviews in Relativity, 9, 3

[3] Shapiro, I. I. (1964). “Fourth Test of General Relativity”. Physical Review Letters, 13, 26

[4] 吴雪峰，陆埮（2006），“伽玛射线暴与爱因斯坦相对论”，物理学进展，第26卷，第1期

[5] Longo, M. J. (1988). “New precision tests of the Einstein equivalence principle from SN1987A”. Physical Review Letters, 60, 173

[6] Krauss, L. M. & Tremaine, S. (1988). “Test of the weak equivalence principle for neutrinos and photons”. Physical Review Letters, 60, 176

[7] Gao, H., Wu, X.-F., & Mészáros, P. (2015). “Cosmic Transients Test Einstein's Equivalence Principle out to GeV Energies”. The Astrophysical Journal, 810, 121

[8] Froeschle, M., Mignard, F., & Arenou, F. (1997). “Determination of the PPN Parameter gamma with the HIPPARCOS Data”. Proceedings of the ESA Symposium `Hipparcos - Venice '97', 13-16 May, Venice, Italy, ESA SP-402 (July 1997), p. 49-52

[9] Wei, J.-J., Gao, H., Wu, X.-F., & Mészáros, P. (2015). “Testing Einstein's Equivalence Principle With Fast Radio Bursts”. Physical Review Letters, 115, 261101

[10] Wei, J.-J., Wang, J.-S., Gao, H., & Wu, X.-F. (2015). “Tests of the Einstein Equivalence Principle Using TeV Blazars”. The Astrophysical Journal Letters, 818, L2

[11] Wu, X.-F. et al. (2016). “Testing Einstein's weak equivalence principle with gravitational waves”. Physical Review D, 94, 024061

[12]https://www.newscientist.com/article/2078129-four-big-cosmology-secrets-gravitational-waves-could-uncover/ 

[13] Abbott, B. P. et al. (2016). “Localization and Broadband Follow-up of the Gravitational-wave Transient GW150914”. The Astrophysical Journal Letters, 826, L13

[14] Adrián-Martínez, S. et al. (2016). “High-energy neutrino follow-up search of gravitational wave event GW150914 with ANTARES and IceCube”. Physical Review D, 93, 122010

[15] Metzger, B. D. & Berger, E. (2012). “What is the Most Promising Electromagnetic Counterpart of a Neutron Star Binary Merger?”. The Astrophysical Journal, 746, 48

[16] Fernández, R. & Metzger, B. D. (2016). “Electromagnetic Signatures of Neutron Star Mergers in the Advanced LIGO Era”. Annual Review of Nuclear and Particle Science, 66, 23-45

另请关注今日头条：早安，爱因斯坦先生！| 引力波天文学之五

扩展阅读

 

测定哈勃常数:引力波对其贡献能有多大？｜引力波天文学之四

揭开“宇宙灯塔”的神秘面纱 – 从中国的FAST说开｜引力波天文学之三

宇宙中闪耀的倩影 -- 伽玛暴 | 引力波天文学之二

诺奖后的下轮豪赌: 寻觅LIGO引力波源的电磁对应体? | 引力波天文学之一

LIGO三剑客荣获诺贝尔物理学奖, 中国学者共享荣光 

陈雁北: 爱因斯坦都不敢想象, 我们真的探测到引力波!

LIGO之父的传奇人生, 下周他会再失诺贝尔吗?

基普·索恩: 科学与艺术的跨界达人

没有他就没有微信, 二战老兵该得炸药奖了

本文系网易新闻·网易号“各有态度”特色内容

媒体如需转载，请联系授权

投稿、授权、合作事宜请联系

service@scholarset.com 或微信ID: scholarset

回复“目录”或“分类”，浏览知社更多精华。长按二维码识别，可以关注/进入公众号进行回复。