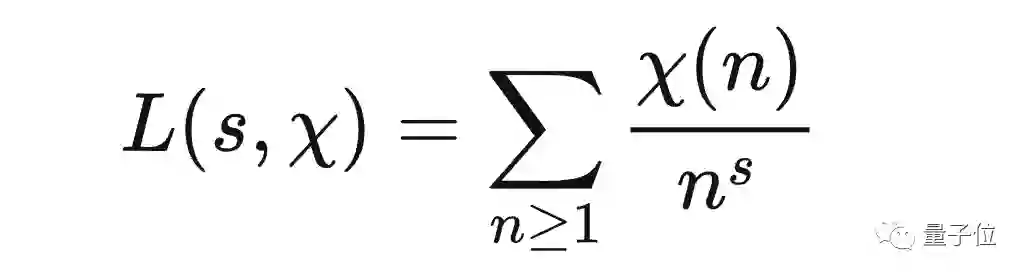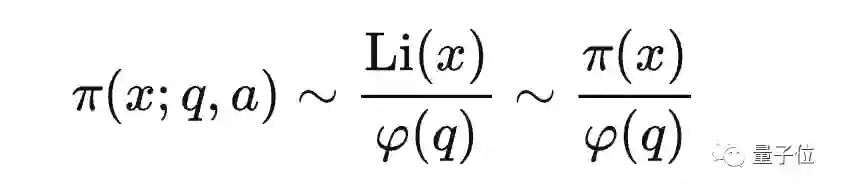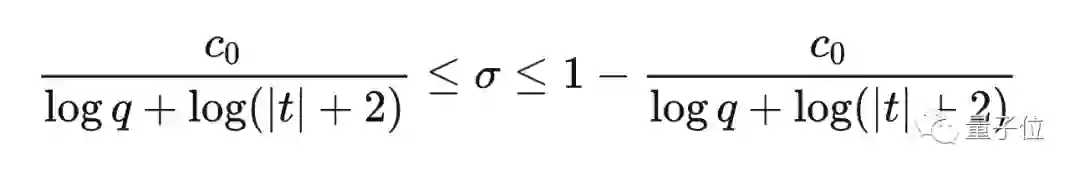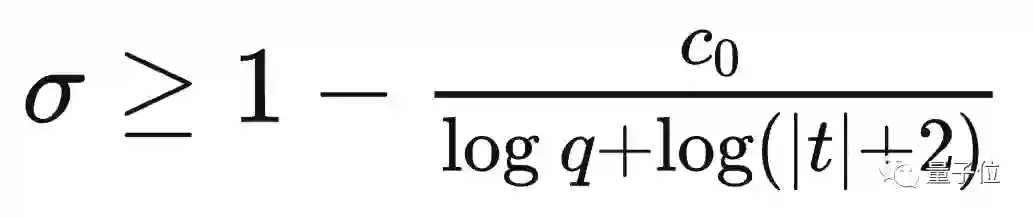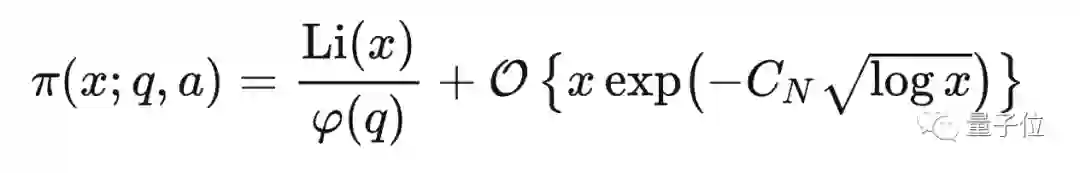张益唐111页零点猜想论文出炉！自称比孪生素数猜想意义更大，每天思考12小时被太太骂

编辑部 发自 凹非寺
量子位 | 公众号 QbitAI

张益唐攻克朗道-西格尔零点猜想的论文，来了！

111页论文，满满当当全是表达式。

论文释出之前，张益唐证明这一黎曼猜想相关问题的消息，早已震动数学界。

就有专家教授表示：

张益唐要是能把Landau-Siegel做出来，就相当于一个人被闪电击中两次。

而张益唐自己也说，攻克朗道-西格尔零点就像是大海捞针。

整个过程我把海底的情况都摸清楚了，后来发现不用这根针，我也能把它做出来。

关于这项成果的意义，张益唐则认为：

比孪生素数猜想的意义更大，朗道-西格尔零点猜想有点像黎曼猜想那样，它一解决，一百个猜想都变成定理了。

完整论文，我们文末奉上。

朗道-西格尔零点猜想

所谓朗道-西格尔零点猜想，简单来说就是黎曼猜想的某种弱形式。

核心要回答的一个问题就是：是否存在一个叫做朗道-西格尔零点的东西。

首先我们设实数σ，t和复数s=σ+it。

根据知乎博主“TravorLZH”的介绍，十九世纪的数学家为了研究素数分布引入了黎曼猜想。

而为了研究等差数列上的素数分布，数学家Dirichlet引入了L函数。

再后来，数学家也发展出了对应的解析工具来说明L函数在σ=1时无零点，从而证明了等差数列上的素数定理：

但对于上面的公式，数学家们依旧是不满意，他们还要继续缩减L函数的非平凡零点的存在区域。

于是前人证明了L函数的非平凡零点基本上都能落在类似于下面公式中的沙漏型的区域：

如果L函数所有的非平凡零点都落在这个区域内，就可以得到带余项的等差数列素数定理。

可惜的是，数学家Edmund Landau发现当X满足特殊性质时其对应的L函数可能会出现落在上面公式之外的异常零点（exceptional zero）。

但幸运的是，Landau证明了对于每个这样的L函数，若下面区域中存在异常零点，则这样的零点只可能出现一个，而且阶数也恰好只能是一。

后来Walfisz利用这个更弱的非零区域得到了一个妥协版的等差数列素数定理：

很明显，这个公式的限制条件要多了许多，所以大家当然希望L函数能够没有异常零点。

由于Landau和Siegel两位数学家在L函数异常零点这个领域里做了开创性的工作，所以异常零点也常常被称为Landau-Siegel零点。

而断言L函数没有异常零点的猜测就被称为Landau-Siegel猜想。

整体来看，其实广义黎曼猜想恰好是Landau-Siegel猜想的充分条件。

但这一个世纪以来的研究表明Landau-Siegel问题可以比黎曼猜想还要难解决。

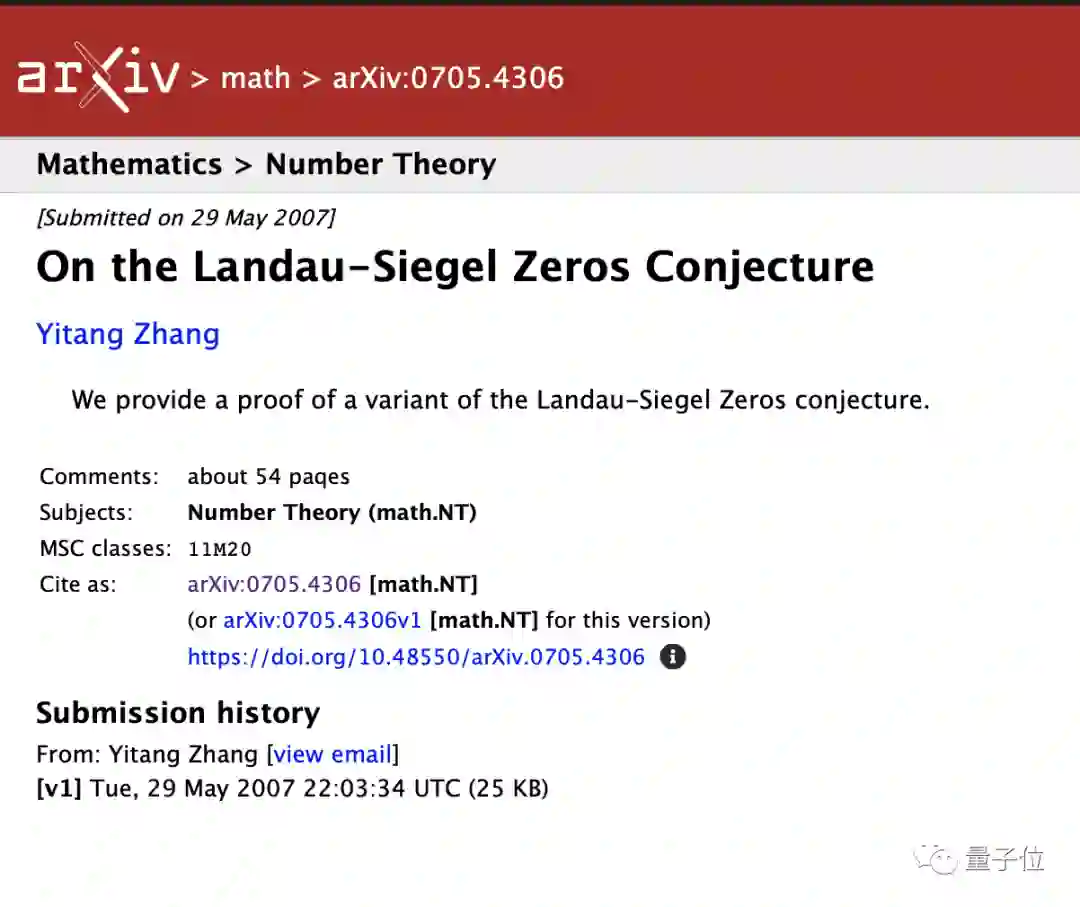
实际上，关于朗道-西格尔猜想，早在07年张益唐就曾在arXiv上发布一篇论文，但是里面的论证有些Bug。

有意思的是，在与北大校友交流时，张益唐透露，一开始，他并没有很系统地去研究这个猜想。

但当今年的新晋菲尔兹奖得主詹姆斯·梅纳德（James Maynard），2020年在他的基础之上，把“孪生素数猜想”的结果又改进了一大步，张益唐心想：

我一定要做出一个更好的东西。

每天12小时思考数学问题

上面这则趣闻，出自北京大学大纽约地区校友会主办的张益唐线上交流座谈。

在其中，还有更多关于这位世界级数学家真实的一面。

在此，我们附上QA环节的部分文字整理：

主持人：研究和生活中觉得最困难的时候是如何坚持下来的呢？

张益唐：如果是指2013年之前（张益唐在2013年证明孪生素数猜想），那可能是我这人天性比较淡泊，我对生活要求很低，所以我也没有太多的困难。

尽管看着别人挣钱多，也不能说没有一点不平衡，但总的讲我还是能坦然处之的。

就是我只要有钱能够花，尽管弄得我太太不高兴（全场大笑），但我还是不觉得太困难，我还是能够坚持下来。

主持人：您如何维持对一件事情的专注？

张益唐：这是一种习惯，某种程度我都觉得是不是我得了一种强迫症。就说你想停都停不下来了。

比如朗道-西格尔零点问题。就是我刚才说大海捞针，最后我也觉得这个针大概是没有了，捞不到了，可还是停不下来。

某种程度上，如果说你一旦真的是完全被吸引住的话，不用刻意怎么样去维持，自然应该就是能够维持的。

主持人：平均每天花多长时间思考数学问题？

张益唐：坦率讲我一天至少思考12个小时以上。

因为我可以不写，不看书，我可以在走路，或者干别的什么事。但我可以一直想这个问题，所以实际上应该是非常长的。长到连我太太都要骂我。

我顺便提一下，就是当我的结果快完成的时候，我几乎是每天晚上做梦都在想这个。而且非常有意思，总觉得这一步还不对，还有问题，弄得挺烦恼，几乎每天都是这样。

主持人：您如何看待学术上的竞争与合作，比如读书时与同门之间的竞争、毕业后与同行之间的竞争。您是如何调整心态？

张益唐：我觉得竞争是正常的。不要说在学术上，就说人有没有心理不平衡的时候，这多少都会有的。

比如我最近遇到的一次，就是那个英国年轻数学家梅纳德（詹姆斯·梅纳德），他在孪生素数这个问题下，一下把我给超过去了，而且超过了不少。

你说当时我的心理是什么样的？我也不管了，反正我已经出名了。（全场大笑）

没有。其实朗道-西格尔零点问题，我以前就开始在想了，但没有那么系统地想。但就是这样，我就下决心我一定还要做出一个更好的东西。

而在今天我敢说这句话，我已经把它做成了。

主持人：关于数学等基础科学的应用化，张师兄怎么看？

张益唐：数学里头很多东西都已经被应用，而且正在发现越来越多的应用，特别在物理在工程上什么的。

即使有一些现在还没有找到应用的，比如像纯粹的解析数论要解决的这些问题，我相信早晚也会发现它是能应用的。但具体这个时间我还不能预测。

另外我们不能说因为这个东西现在暂时没有应用，或者找不到应用，就轻视它。

基础数学、基础科学的这个研究，它不仅将来会具有潜在的应用，它也是衡量一个民族，一个国家，你的文化程度，你的发达程度，这一点是不能忽略的。

论文传送

最后，奉上张益唐这篇Landau-Siegel零点猜想完整论文。

在量子位公众号后台回复张益唐或零点猜想，即可获取论文PDF。

另外，此番有关朗道-西格尔零点猜想，11月8日，张益唐也会面向北大师生专门做一场学术报告。B站会有同步直播，感兴趣的小伙伴可以马克起来~

△图源：北京国际数学研究中心BICMR

— 完 —

MEET 2023 大会启动

邀你共论智能产业穿越周期之道

今年12月，MEET2023智能未来大会将再度邀请智能科技产业、科研、投资领域大咖嘉宾，共同探讨人工智能行业破局之道。

欢迎智能科技企业参会，分享突破性成果，交流时代级变革，共襄盛会！点击链接或下方图片查看大会详情：

量子位「MEET 2023智能未来大会」启动，邀你共论智能产业穿越周期之道

点这里关注我 👇 记得标星噢 ~

一键三连「分享」、「点赞」和「在看」

科技前沿进展日日相见 ~