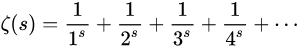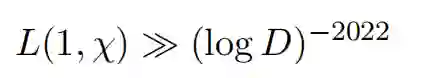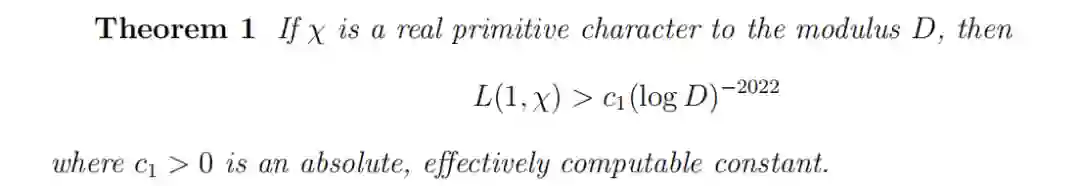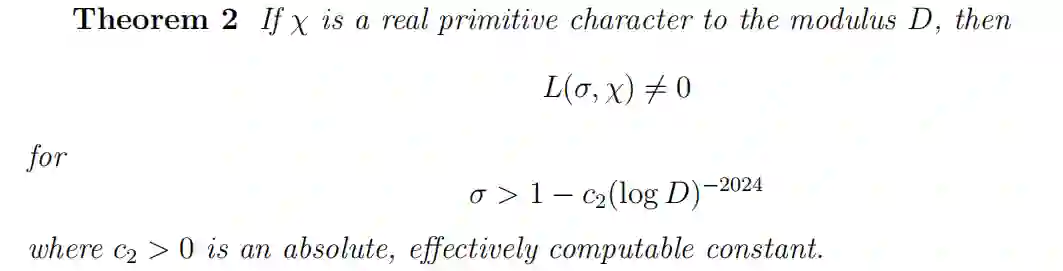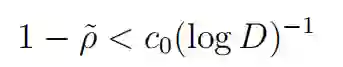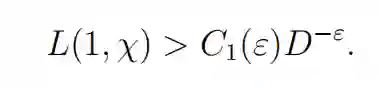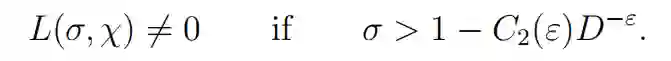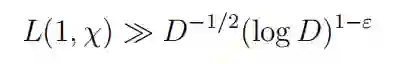111页，张益唐攻克朗道-西格尔零点猜想论文公布，8号B站直播开讲

机器之心报道

编辑：杜伟、陈萍

论文是放出了，怎奈看不懂啊！！！

终于！数学家张益唐攻克朗道 - 西格尔（Landau-Siegel）零点猜想的预览版论文放出了。

11 月 5 日，张益唐为山东大学数学学院等机构进行了学术报告。这篇长达 111 页、18 个章节的论文也开始在网上传播，我们终于见到了它的庐山真面目。

论文地址：https://drive.google.com/file/d/1vTLoh_Cpw6Zr436rD7FnjzND6ngY2VG8/view

张益唐在致谢中表示，「本证明的基本思路是在他 2014 年访问普林斯顿高等研究院期间初步形成的。他非常感谢普林斯顿高等研究院为自己提供了良好的学术条件，并感谢该院教授 Peter Sarnak 的鼓励。」

10 月中旬，在北京大学大纽约地区校友会主办的张益唐线上交流座谈上，张益唐确认自己「在本质上已经解决了 Landau-Siegel 零点问题，不过是以一种弱一点的形式。」

他还认为，Landau-Siegel 零点猜想的解决比孪生素数猜想的意义更大。这就有点像黎曼猜想，它一解决，一百个猜想就变成定理了。

另外，据澎湃新闻向北京国际数学研究中心主任、北京大学数学英才班委员会主任田刚院士证实，论文已经提交至预印本网站 arXiv，预计下周一将正式上线。

论文还要经过同行评审，如果通过，势必将成为数学史上的一大里程碑式突破。

11 月 8 日，张益唐还将为北京大学数学科学学院、北京国际数学研究中心进行「关于郎道 - 西格尔零点猜想」学术报告，并通过 B 站等平台线上直播。

直播地址：https://live.bilibili.com/25879004

论文介绍

郎道 - 西格尔零点猜想是黎曼猜想的某种弱形式，核心要回答的问题即「是否存在一个叫做朗道 - 西格尔零点的东西？」

这里先介绍一下黎曼猜想，该猜想是数学家黎曼于 1859 年提出，是关于黎曼ζ函数ζ(s) 的零点分布的猜想，它是数学中一个重要而又著名的未解决的问题，有猜想界皇冠之称。德国数学家戴维 · 希尔伯特在第二届国际数学家大会上提出的 20 世纪数学家应当努力解决的 23 个数学问题，其中便包括黎曼猜想。现今克雷数学研究所悬赏的世界七大数学难题中也包括黎曼猜想。

多少年来，它吸引了许多出色的数学家为之绞尽脑汁，但都没有成功。

关于该猜想，黎曼发现，素数分布的规律就隐藏在某个函数的零点分布中。这个函数就是黎曼 ζ 函数：

黎曼将该函数解析延拓至整个复平面，并指出：黎曼ζ函数的非平凡零点（是指 s 不为 - 2、-4、-6‧‧‧ 等点的值，这些都是平凡零点）的实数部分都是 1/2。也就是说，这些非平凡零点都分布在复平面的 Re(z)=1/2 的直线上。

要证伪黎曼猜想，只需要找到一个不在 Re(z)=1/2 这条直线上的非平凡零点即可，只不过目前还没有发现这样的零点。

黎曼猜想及推广形式的成立是现有很多数学命题的前提。如果黎曼猜想及其推广形式被证明，这些数学命题都将变为数学定理；反之，一旦黎曼猜想被证伪，将有 1000 多个数学命题成为黎曼猜想的「陪葬品」。

我们回到这篇论文。论文摘要中是这样介绍的：设χ是模（modulus）D 的一个实本数。则存在证明：

这里隐含的常数是绝对的并且可以有效地计算。

在证明中，L(1， χ) 的下界首先与 Dirichlet L 函数族的零点在一定区域内的分布有关，并得到了关于连续零点间间隙的一些结果。然后，通过对大筛型的某一离散均值的求值，得到 L(1， χ) 过小时的矛盾。

张益唐主要贡献如下：根据知乎网友的总结，首先是 L 函数在 1 点处的下界估计。

相应的有关于实轴上非零区域的直接推论：

下面是论文的 Introduction 部分。设χ是模 D 的一个实本数（real primitive character）。朗道 - 西格尔零点猜想是讨论 L 函数（Dirichlet L-function L(s, χ) ）在以下区域是否存在零点：

其中 c_0 > 0 是一个绝对常数。这样的零点被称为朗道 - 西格尔零点。确定 Dirichlet L 函数的零点自由区域的典型方法由于内在原因无法消除朗道 - 西格尔零点。

著名的西格尔定理断言，对于任何ε > 0，存在一个正数 C_1(ε) 使：

这意味着，对于任意的ε > 0，存在一个正数 C_2(ε) 使：

然而，西格尔的证明过程本质上涉及到某些假设，这使得西格尔定理的结果完全无效。众所周知，朗道 - 西格尔零点的不存在意味着有以下关于下界估计的推论：

在χ(−1)=−1 的情况下，Goldfeld 和 Gross、Zagier 证明了这一点：

对于任意ε > 0，其中隐含的常数是可以有效计算的。

以上就是论文的开始部分。感兴趣的小伙伴可以查阅原论文以获得更多内容。

网友：完全看不懂，怎么评价

张益唐攻克 Landau-Siegel 零点猜想的相关论文发布后，便登上了知乎热榜。不明觉厉的网友纷纷表示了对张益唐大佬的「膜拜」。

有人表示，「把推导公式放在面前都看不懂。」

而关于解决 Landau-Siegel 零点猜想有哪些具体意义，更多的外行网友只能期待未来解析数论专家的介绍了。

同时，更多的网友对张益唐年近 70 仍潜心数学研究表示由衷地钦佩！

参考链接：

https://www.zhihu.com/question/564799818

https://www.thepaper.cn/newsDetail_forward_20609386

即将毕业，请回答！小红书正在呼唤懂AI的你

11月19日16:00 - 19:30 ，北京市海淀区成府路28号2层 PAGEONE（五道口店），小红书REDtech青年技术沙龙，设置「报告+对谈+青年学子晚餐交流会」等丰富板块，诚邀高校顶尖毕业生们来现场与顶尖学者、小红书技术团队大神欢聚畅谈！

顺便聊聊，在小红书，你将如何高速成长？

• 有行业竞争力的薪酬

• 优先落户等硬核福利

• 专属个人成长计划

• 丰富技术场景实践机会

• 全球顶尖企业和高校实验室深度交流通路

• ……

小红书携丰富资源，全面助力高校顶尖毕业生勇探技术高峰！

赶快扫描下方二维码，与小红书相约「宇宙中心」！

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com