多元线性回归预测：餐馆营业额与多因素实战

会员服务 ·

多元线性回归预测：餐馆营业额与多因素实战

2019 年 1 月 8 日 R语言中文社区

作者：herain R语言中文社区专栏作者

知乎ID：https://www.zhihu.com/people/herain-14

前言

上篇我们用一元线性回归预测销售收入与广告支出实战，但世界是复杂的，有因有果，因果迭交，我们常说事或物是多种因素共同作用的结果，今天我们从统计学角度，去分析多种因素是怎么样作用一种事物，产生不一样的结果。

综述

以餐馆营业额作为果（y= 日均营业额/万元），周边居民人数（x1 /万人），用餐平均支出（x2 / 元/人），周边居民月平均收入（x3/ 元），周边餐馆数（x4/ 个），距市中心距离（x5/ km）作为因素，来探索因与果之间的回归模型，发现规律，改善餐馆营销方式，提高餐馆的营业额。

分析步骤

餐馆营业额与多因素的回归模型分析步骤：

1.确定所关注的因变量y 和影响因变量的k个自变量

2.假定因变量y 与 k 个自变量之间为线性关系，并建立线性关系模型

3.对模型进行估计和检验

4.判别模型中是否存在多重共线性，如果存在，进行处理

5.利用回归方程进行预测

6.对回归模型进行诊断

1 确定因变量y和影响因变量的k个自变量

1.1 确定因变量和自变量

y:餐馆营业额作为果（y= 日均营业额/万元）

k个自变量为：

周边居民人数（x1 /万人）
用餐平均支出（x2 / 元/人）
周边居民月平均收入（x3/ 元）
周边餐馆数（x4/ 个）
距市中心距离（x5/ km）

1.2 分析的数据：

   index    y    x1    x2    x3 x4   x5
1      1 53.2 163.0 168.6  6004  5  6.5
2      2 18.5  14.5  22.5   209 11 16.0
3      3 11.3  88.2 109.4  1919 10 18.2
4      4 84.7 151.6 277.0  7287  7 10.0
5      5  7.3  79.1  17.4  5311 15 17.5
6      6 17.9  60.4  93.0  6109  8  3.6
7      7  2.5  53.2  21.5  4057 17 18.5
8      8 27.3 108.5 114.5  4161  3  4.0
9      9  5.9  48.7  61.3  2166 10 11.6
10    10 23.9 142.8 129.8 11125  9 14.2
11    11 69.4 214.7 159.4 13937  2  2.5
12    12 20.6  65.6  91.0  4000 18 12.0
13    13  1.9  13.2   6.1  2841 14 12.8
14    14  3.0  60.9  60.3  1273 26  7.8
15    15  7.3  21.2  51.1  2404 34  2.7
16    16 46.2 114.3  73.6  6109 12  3.2
17    17 78.8 299.5 171.7 15571  4  7.6
18    18 11.1  78.9  38.8  4228 11 11.0
19    19  8.6  90.0 105.3  3772 15 28.4
20    20 48.9 160.3 161.5  6451  5  6.2
21    21 22.1  84.0 122.6  3275  9 10.8
22    22 11.1  78.9  38.8  4228 10 33.7
23    23  8.6  90.0 105.3  3772 14 16.5
24    24 48.9 160.3 161.5  6451  6  9.3
25    25 22.1  84.0 122.6  3275 10 11.6

2 建立线性关系模型

公式：

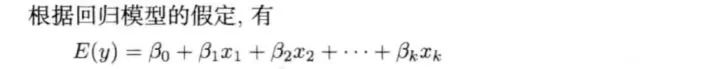
2.1 绘制多个变量的相关图：

> library(corrgram)
> corrgram(example10_1[2:7], order=T, lower.panel=panel.shade,upper.panel=panel.pie,text=panel.txt)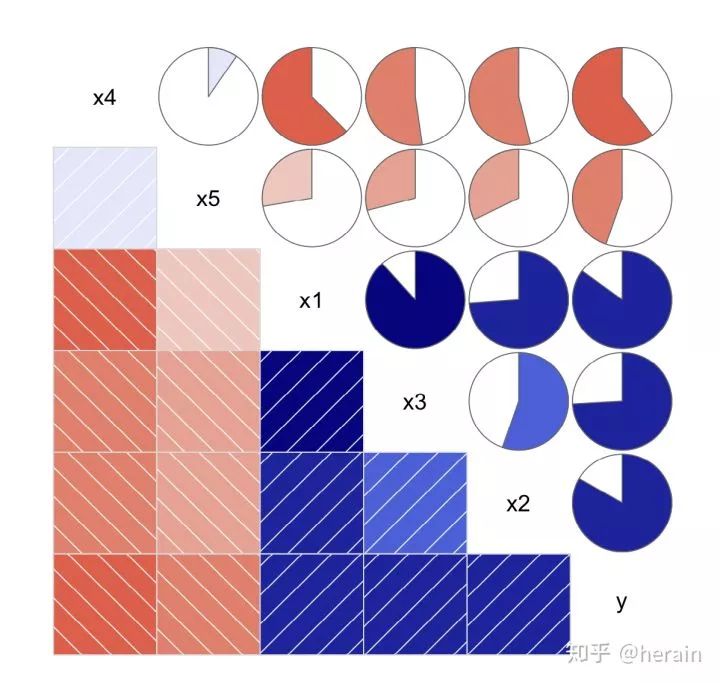

解读相关系数矩阵图，请参考搜索，获取了解。蓝色表示正相关，红色表示负相关，对应颜色的饼图表示相关的度。

2.2 建立回归模型（检测报告，模型进行估计和检验用到了如下检测结果）：

检测报告：

#回归模型拟合
> fit1 <- lm(y~x1+x2+x3+x4+x5, data=example10_1)
> summary(fit1)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4 + x5, data = example10_1)

Residuals:
     Min       1Q   Median       3Q      Max 
-16.7204  -6.0600   0.7152   3.2144  21.4805 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept)  4.2604768 10.4679833   0.407  0.68856   
x1           0.1273254  0.0959790   1.327  0.20037   
x2           0.1605660  0.0556834   2.884  0.00952 **
x3           0.0007636  0.0013556   0.563  0.57982   
x4          -0.3331990  0.3986248  -0.836  0.41362   
x5          -0.5746462  0.3087506  -1.861  0.07826 . 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 10.65 on 19 degrees of freedom
Multiple R-squared:  0.8518,    Adjusted R-squared:  0.8128 
F-statistic: 21.84 on 5 and 19 DF,  p-value: 2.835e-07

#计算回归系数的置信区间
> confint(fit1, level=0.95)
                    2.5 %       97.5 %
(Intercept) -17.649264072 26.170217667
x1           -0.073561002  0.328211809
x2            0.044019355  0.277112598
x3           -0.002073719  0.003600932
x4           -1.167530271  0.501132297
x5           -1.220868586  0.071576251

#输出方差分析表
> anova(fit1)
Analysis of Variance Table

Response: y
          Df  Sum Sq Mean Sq F value    Pr(>F)    
x1         1 10508.9 10508.9 92.7389 9.625e-09 ***
x2         1  1347.1  1347.1 11.8878  0.002696 ** 
x3         1    85.4    85.4  0.7539  0.396074    
x4         1    40.5    40.5  0.3573  0.557082    
x5         1   392.5   392.5  3.4641  0.078262 .  
Residuals 19  2153.0   113.3                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

从检验结果可以看出 x1，x2，x5 对 y 的总误差平方和贡献显著。

2.3 回归模型方程式：

计算：y = 4.2604768 + 0.1273254*x1 + 0.1605660*x2 + 0.0007636x3 -0.3331990 x4 -0.5746462 * x5

3 对模型进行估计和检验

3.1 拟合优度检验

多重决定系数是多元线性回归中回归平方和SSR 占总平方和SST的比例，计算公式为：

它表示因变量y的总误差中被多少个自变量共同解释的比例。

为避免增加自变量而高估多重决定系数，统计学家使用样本量n和自变量的个数k 去调整多重决定系数：

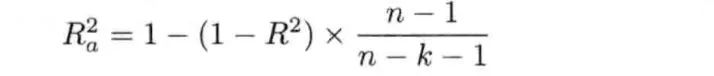
计算知：多重决定系数为：0.8518，说明日均营业额时与周边居民人数，用餐平均支出，周边居民月平均收入，周边餐馆数和距离市中心这5个自变量模型的拟合度较高。

Multiple R-squared: 0.8518, Adjusted R-squared: 0.8128

3.2 估计标准误：

标准误就是指残差的标准差，计算公式：

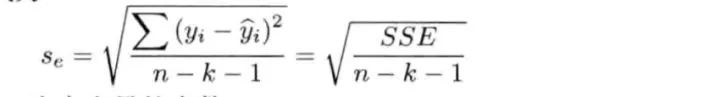
计算知：估计的标准误差为：10.65，根据建立的多元线性回归方程，周边居民人数，用餐平均支出，周边居民月平均收入，周边餐馆数和距离市中心这5个自变量预测日均营业额时，平均的预测误差为10.65万元

Residual standard error: 10.65 on 19 degrees of freedom

3.3 模型的显著性检验

包含如下检验：线性关系检验，回归系数检验。请参考（2.2处：检测报告）诠释如下两种假设，此次省略具体说明。

3.4 模型诊断

绘制残差图诊断模型

> par(mfrow=c(1,2), mai=c(0.8,0.8,0.4,0.1),cex=0.8,cex.main=0.7)
> plot(fit1,which=1)
> plot(fit1,which=2)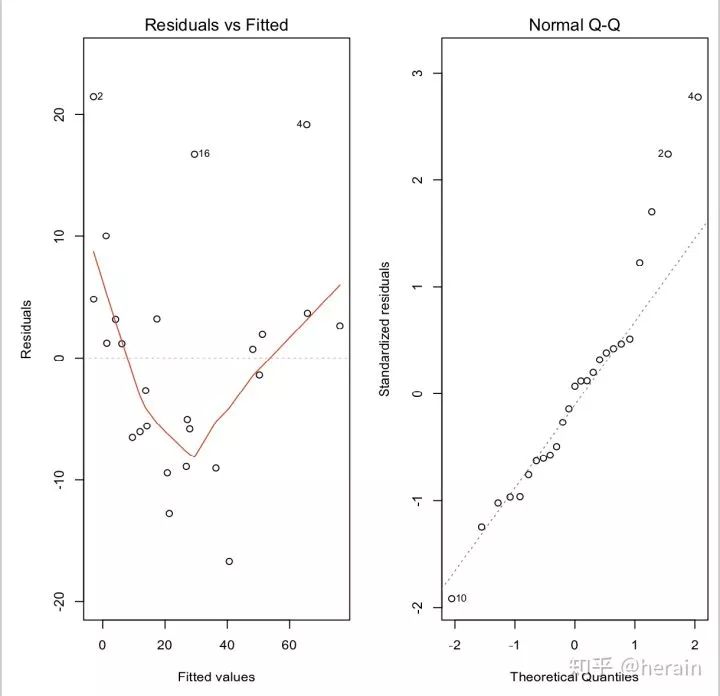

在图中发现点2，4，16具有较大残差，残差的正态性存在问题（可以考虑重建模型，或者剔除较大残差值），如下我们剔除点 2，4 重新建立回归模型：

#再次绘制残差图
> par(mfrow=c(1,2), mai=c(0.8,0.8,0.4,0.1),cex=0.8,cex.main=0.7)
> plot(newfit1,which=1)
> plot(newfit1,which=2)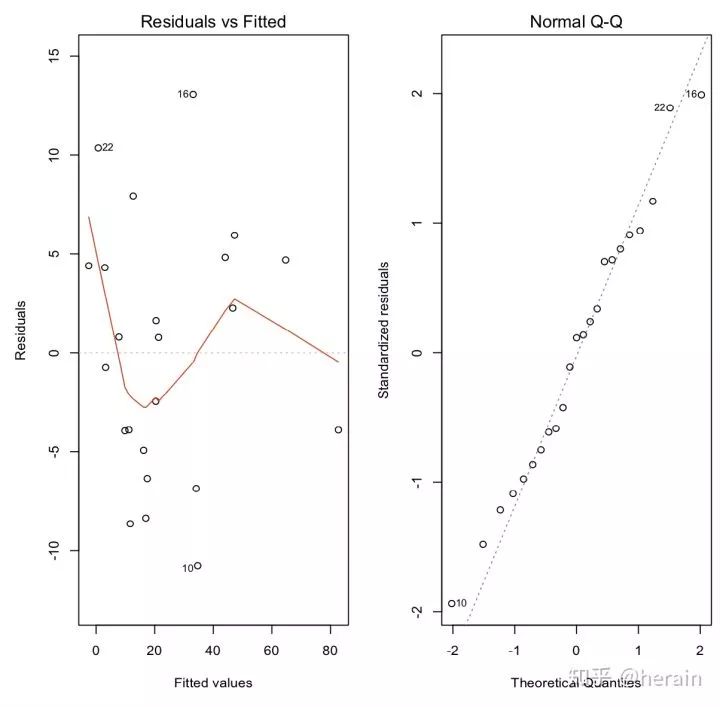

4 判别模型中是否存在多重共线性

4.1 判别的重要性

变量之间的高度相关性，造成回归结果的混乱。多重共性性可能对参数估计值的正负号产生影响。

4.2 识别共线性和处理

#1，自变量之间的相关系数及其检验
> library(psych)
> corr.test(example10_1[3:7], use="complete")
Call:corr.test(x = example10_1[3:7], use = "complete")
Correlation matrix 
  x1x2x3x4x5
x1  1.00  0.74  0.88 -0.62 -0.28
x2  0.74  1.00  0.55 -0.54 -0.32
x3  0.88  0.55  1.00 -0.52 -0.29
x4 -0.62 -0.54 -0.52  1.00  0.10
x5 -0.28 -0.32 -0.29  0.10  1.00
Sample Size 
[1] 25
Probability values (Entries above the diagonal are adjusted for multiple tests.) 
 x1   x2   x3   x4   x5
x1 0.00 0.00 0.00 0.01 0.47
x2 0.00 0.00 0.03 0.03 0.46
x3 0.00 0.00 0.00 0.04 0.47
x4 0.00 0.01 0.01 0.00 0.65
x5 0.18 0.12 0.16 0.65 0.00

 To see confidence intervals of the correlations, print with the short=FALSE option

#2，考察回归系数的显著性
#3，分析回归系数的正负号
#4，用容忍度和方差膨胀因子（VIF）,VIF 大于10 存在严重的共线性:
> library(car)
载入需要的程辑包：carData
载入程辑包：‘car’
The following object is masked from ‘package:psych’:logit

> library(carData)
> vif(fit1)
  x1   x2   x3   x4   x5 
8.233159 2.629940 5.184365 1.702361 1.174053 
> 1/vif(fit1)
   x1x2x3x4x5 
0.1214601 0.3802368 0.1928877 0.5874195 0.8517500 
>

如上分析数据可知，不存在严重的共线性问题

4.3 变量的选择与逐步回归

建立模型之前就有选择的确定进入模型的自变量，也可以避免多重共线性问题，变量的选择方法主要有 向前选择，向后剔除，逐步回归 等。

逐步回归以赤池信息准则AIC为选择标准，选择AIC最小的变量建立模型，计算公式为：

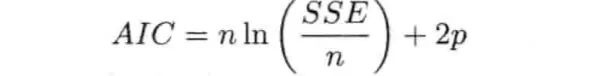
式中，n为样本量；p为模型中参数的个数（包括常数项）

#对模型fit1进行逐步回归
> fit2 <-step(fit1)
Start:  AIC=123.39
y ~ x1 + x2 + x3 + x4 + x5

       Df Sum of Sq    RSS    AIC
- x3    1     35.96 2189.0 121.81
- x4    1     79.17 2232.2 122.30
<none>              2153.0 123.39
- x1    1    199.42 2352.4 123.61
- x5    1    392.54 2545.6 125.58
- x2    1    942.22 3095.2 130.47

Step:  AIC=121.81
y ~ x1 + x2 + x4 + x5

       Df Sum of Sq    RSS    AIC
- x4    1     78.22 2267.2 120.69
<none>              2189.0 121.81
- x5    1    445.69 2634.7 124.44
- x2    1    925.88 3114.9 128.63
- x1    1   1133.27 3322.3 130.24

Step:  AIC=120.69
y ~ x1 + x2 + x5

       Df Sum of Sq    RSS    AIC
<none>              2267.2 120.69
- x5    1    404.28 2671.5 122.79
- x2    1   1050.90 3318.1 128.21
- x1    1   1661.83 3929.0 132.43
> 

> fit2 <- lm(y~x1+x2+x5, data=example10_1)
> summary(fit2)

Call:
lm(formula = y ~ x1 + x2 + x5, data = example10_1)

Residuals:
    Min      1Q  Median      3Q     Max 
-14.027  -5.361  -1.560   2.304  23.001 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.68928    6.25242  -0.270  0.78966    
x1           0.19022    0.04848   3.923  0.00078 ***
x2           0.15763    0.05052   3.120  0.00518 ** 
x5          -0.56979    0.29445  -1.935  0.06656 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 10.39 on 21 degrees of freedom
Multiple R-squared:  0.8439,    Adjusted R-squared:  0.8216 
F-statistic: 37.85 on 3 and 21 DF,  p-value: 1.187e-08


#逐步回归的方差分析
> anova(fit2)
Analysis of Variance Table

Response: y
          Df  Sum Sq Mean Sq F value    Pr(>F)    
x1         1 10508.9 10508.9 97.3392 2.452e-09 ***
x2         1  1347.1  1347.1 12.4775  0.001976 ** 
x5         1   404.3   404.3  3.7447  0.066558 .  
Residuals 21  2267.2   108.0                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

根据R的逐步回归结果，得到最终的估计方程：

y = -1.68928 + 0.19022 * x1 + 0.15763 * x2 - 0.56979 * x3

> par(mfcol=c(1,2),cex=0.7)
> plot(fit2, which=1)
> plot(fit2,which=2)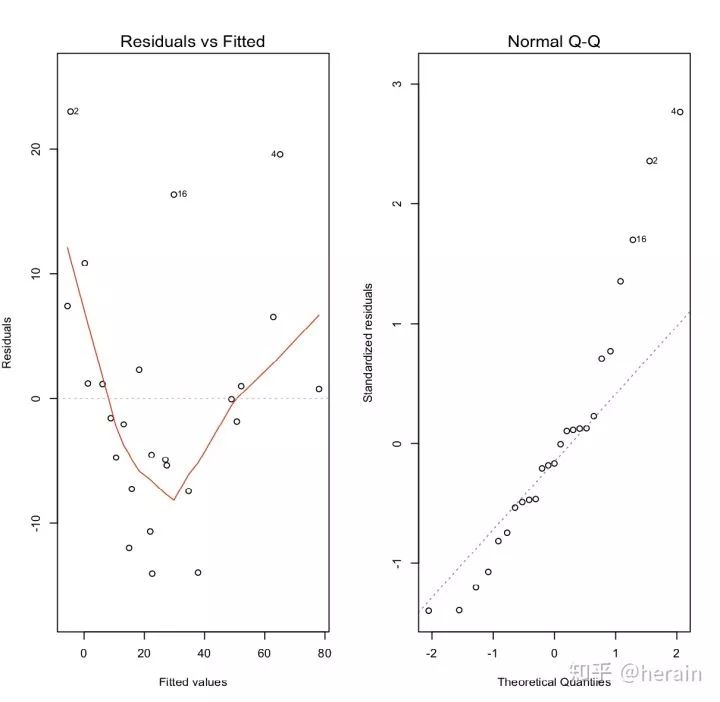

4.4 多模型的比较

完全模型，简化模型

#模型方差对比
> anova(fit1, fit2)
Analysis of Variance Table

Model 1: y ~ x1 + x2 + x3 + x4 + x5
Model 2: y ~ x1 + x2 + x5
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1     19 2153.0                           
2     21 2267.2 -2   -114.17 0.5038 0.6121

#机器的交叉验证
#五折交叉验证
#AIC对比
> AIC(fit1, fit2)
     df      AIC
fit1  7 196.3408
fit2  5 193.6325

对比数据，得知 fit2 模型的拟合的更好。

5 利用回归方程进行预测

基于多点的点估计，求出区间估计（均值的区间估计，个别值的预测区间）

#计算置信区间和预测区间
> x<- example10_1[,c(3,4,7)]
> pre<-predict(fit2)
> res<-residuals(fit2)
> zre<-rstandard(fit2)
> con_int<-predict(fit2,x,interval="confidence",level=0.95)
> pre_int<-predict(fit2,x,interval="prediction",level=0.95)
> mysummary<-data.frame(日均营业额=example10_1$y, 点预测值=pre,残差=res,标准化残差=zre, 
置信下限=con_int[,2], 置信上限=con_int[,3], 预测下限=pre_int[,2], 预测上限=pre_int[,3])
> round(mysummary,3)
   日均营业额 点预测值残差 标准化残差 置信下限 置信上限 预测下限 预测上限153.2   52.189   1.011  0.102   45.457   58.921   29.557   74.822
218.5   -4.501  23.001  2.359  -11.9692.967  -27.363   18.361
311.3   21.963 -10.663 -1.072   15.685   28.240   -0.539   44.464
484.7   65.114  19.586  2.766   49.300   80.928   38.337   91.891
5 7.36.128   1.172  0.122   -2.283   14.540  -17.059   29.316
617.9   22.408  -4.508 -0.466   14.581   30.235   -0.574   45.390
7 2.51.278   1.222  0.125   -6.1138.670  -21.559   24.116
827.3   34.719  -7.419 -0.747   28.400   41.038   12.206   57.232
9 5.9   10.628  -4.728 -0.4724.904   16.351  -11.726   32.981
10   23.9   37.843 -13.943 -1.390   32.193   43.493   15.509   60.178
11   69.4   62.852   6.548  0.709   52.939   72.766   39.079   86.626
12   20.6   18.296   2.304  0.229   13.036   23.556   -3.943   40.535
131.9   -5.510   7.410  0.771  -13.6942.674  -28.616   17.596
143.0   14.956 -11.956 -1.2028.687   21.224   -7.543   37.455
157.38.860  -1.560 -0.169   -1.050   18.770  -14.913   32.632
16   46.2   29.831  16.369  1.699   21.745   37.9176.759   52.903
17   78.8   78.016   0.784  0.112   62.105   93.927   51.182  104.850
18   11.1   13.167  -2.067 -0.2096.420   19.915   -9.470   35.805
198.6   15.847  -7.247 -0.8154.670   27.024   -8.481   40.175
20   48.9   50.727  -1.827 -0.184   44.205   57.250   28.156   73.299
21   22.1   27.461  -5.361 -0.536   21.671   33.2515.090   49.831
22   11.10.233  10.867  1.354  -13.486   13.953  -25.362   25.829
238.6   22.627 -14.027 -1.395   17.181   28.0730.344   44.911
24   48.9   48.961  -0.061 -0.006   42.722   55.200   26.470   71.452
25   22.1   27.005  -4.905 -0.490   21.220   32.7904.636   49.374
#求 x1=50, x2=100, x5=10 时的日均营业额的点预测值，置信区间和预测区间（新值预测）
> x0<-data.frame(x1=50,x2=100,x5=10)
> predict(fit2, x0)
   1 
17.88685 
> predict(fit2,x0, interval="confidence", level=0.95)
   fit  lwr  upr
1 17.88685 10.98784 24.78585
> predict(fit2,x0, interval="prediction", level=0.95)
   fit   lwr  upr
1 17.88685 -4.795935 40.56963
>

6 哑变量回归

代码化的类别变量成为哑变量或者虚拟变量，在回归模型中使用哑变量时称为哑变量回归或者虚拟变量回归。

写在最后：

至此，多元线性回归预测也完成了，欢迎大家指正，请各位多多转发，给我好看。

公众号后台回复关键字即可学习

回复爬虫         爬虫三大案例实战
回复 Python 1小时破冰入门

回复数据挖掘   R语言入门及数据挖掘
回复人工智能   三个月入门人工智能
回复数据分析师   数据分析师成长之路
回复机器学习      机器学习的商业应用
回复数据科学      数据科学实战
回复常用算法      常用数据挖掘算法