时间自适应卷积：比自注意力更快的特征提取器

论文标题：

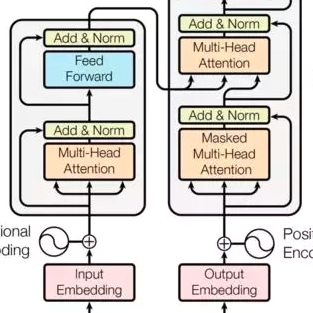
Time-aware Large Kernel Convolutions

论文作者：

Vasileios Lioutas, Yuhong Guo

论文链接：

https://arxiv.org/pdf/2002.03184v1.pdf

---

在本文，我们介绍一篇非常有趣的工作：使用“时间自适应”的卷积去替换Transformer中的自注意力，从而将时间复杂度从降低到O(n)，极大加快了文本生成的速度，同时还得到了非常好的效果。

在数据集WMT En-De, En-Fr和IWSLT De-En上取得了和当前最优相同的结果。

Transformer的时间复杂度

作为大家熟悉的老朋友，Transformer在各种NLP模型、任务上已经被反复提及了。

Transformer使用了自注意力(Self-attention)去建模每个字符和所有字符的关系，从而，它的时间复杂度是的。

显然，这在模型运行的过程中是一笔不可忽略的开销，尤其当句子长度很大的时候，运行Transformer的时间开销是非常大的。

那么，有没有什么方法既能实现Transformer的效果，又能加快速度吗？

动态卷积给出了一个比较好的答案：使用卷积网络建模语义关系，从而将复杂度降低到O(kn)，这里k是卷积核大小。

那么，有没有进一步减小时间开销呢？为此，本文继续从卷积网络出发，提出一种时间自适应的卷积：对每个时间步（即每个位置的字符），动态地预测得到它的卷积核大小，进而利用现有的“并行点缀和”技术降低时间复杂度，使其达到最理想的O(n)。

在降低时间开销的同时，本方法还能达到和当前最优相同的结果，既高效又强大。

总的来说，本文贡献如下：

• 提出时间自适应卷积，对每个字符得到其不同的卷积核大小；

• 极大降低自注意力的时间开销，将复杂度降低到了O(n)，同时还有更少的内存开销；

• 在WMT En-De, En-Fr和IWSLT De-En和WikiText-103上实现了和当前最优十分相近的结果。

在阅读完本文后，读者可以思考一个简单的问题：为什么说这种方法可以实现线性复杂度O(n)？

时间自适应卷积

设输入是长度为 n 的文本，每个都是 d 维向量，就是所谓的时间步。

为此降低编码时间开销，我们首先直接考虑把第 i 个时间步周围的向量相加（相当于一个窗口）：

其中是窗口的两端。

当然，如果对每个时间步 i 都单独相加，这就非常低效，因为有很多项被重复相加。为此，我们直接考虑前缀和：

那么，现在就可以写成：

我们现在想要对每个时间步 i，它的窗口大小是不同的，所以需要为每个计算它的窗口。由于直接计算窗口大小的绝对值不方便，我们转而计算其相对值：

其中，是相对大小，是最大允许的窗口大小。

由于计算得到的实值，我们需要把它转化为整数。下面，我们就从这实值附近采样整数：

这里。上述操作都是可微的。

然而，这种方法的问题是，随着模型层数的增加，向量的和会越来越大，导致模型无法收敛。所以，我们还需要对得到的结果归一化：

此外，对得到的加以Dropout也有助于过拟合。

类似Transformer，该方法也可以应用到多头机制上。这只需要把原始的输入分成若干组，然后对所有组并行操作即可，下图是一个示例：

图中有两个头，分别是绿色和蓝色，各自的绝对窗口大小分别在左右。

在解码的时候，只需要令即可。

实验

本文在机器翻译数据集WMT English to German (En-De), WMT English to French (En-Fr) and IWSLT German to English (De-En)和语言模型数据集WikiText-103上实验。具体实验细节详见论文。

下面是在WMT上的实验结果。可以看到，在参数量几乎相同的情况下，本方法（TaLK）实现了几乎和当前最优结果相同的结果（实际上还要更快）。

而在IWSLT De-En上，本方法达到了35.5的BLEU值，比之前最好的35.2更高。

而在语言模型上，在相同的参数量下，本方法取得了最好的结果，为20.3的PPL，如下表所示：

下面我们重点比较各方法的编码时间和内存上的开销，结果如下表所示。

首先看内存开销，随着句子长度的增加，本方法相比自注意力就更加有优势，并且比动态卷积还要略好。

再看每秒迭代次数，在 n=10,100 的时候，本方法每秒迭代次数大概是自注意力和动态卷积的两倍。

在 n=1000 的时候，是自注意力的四倍，是动态迭代的两倍；而在 n=10000 时，自注意力直接OUt of Memory，而本方法依旧坚挺。

最后我们来看看本方法各组成的作用，如下表所示。显然，没有归一化，模型原地狗带，无法收敛。增大窗口最终效果所有帮助，其他方面的技巧似乎帮助不太大。

小结及思考题

本文提出一种时间自适应的卷积，在每一个时间步，都动态地得到当前的卷积大小，并使用前缀和实现了 O(n) 的复杂度。在机器翻译和语言模型的实验上表明了该方法又快又好，还能节省内存开销。

至于为什么说这种方法只有线性复杂度：首先，我们需要对每个时间步操作，而对它而言，我们只需要计算一个前缀和的差即可，而前缀和是预先计算得到的，所以可以看作是一个常量。从而总的来说，编码的复杂度就是 O(n)。

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。