在 TensorFlow 中模拟宇宙

客座博文 / 来自伯克利宇宙物理中心 (Berkeley Center for Cosmological Physics)、CosmoStat 实验室 (CosmoStat Laboratory) 和劳伦斯·伯克利国家实验室 (Lawrence Berkeley National Laboratory) 的 Chirag Modi、François Lanusse、Mustafa Mustafa、Uroŝ Seljak

简介

在宇宙学研究中，在计算机上进行数值模拟[1] 是个重要手段，这是宇宙学家用于分析理解宇宙测绘收集的大量数据的基本工具。此类模拟在计算上的花销通常特别高昂，并且往往需要在大型超级计算机上离线运行。但是，假如我们可以以超快的速度执行此类模拟级，并实现与机器学习组件集成到一个统一框架内，会怎样？这就是全新的 N 体宇宙学模拟代码 FlowPM[2] 要完成的目标。在本文中，我们将向您展示如何在 TensorFlow 中模拟自己的微型宇宙，并展望这将为宇宙学带来的新前景。

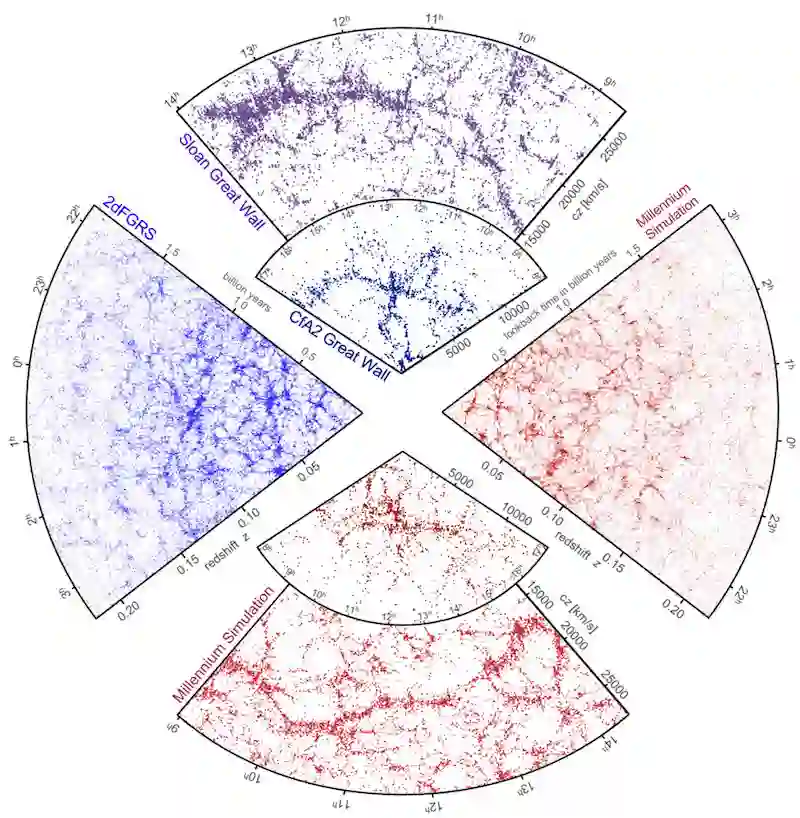
图 1：（蓝色）2dFGRS 测绘计划中观察到的宇宙结构。（红色）千年 N 体模拟中生成的对应结构

N 体宇宙模拟

宇宙学的 N 体模拟展示出宇宙从大爆炸中诞生到至今的发展演化过程。宇宙学家根据物质的初始分布将大量粒子分布在一个方框内，然后模拟这些粒子随时间推移及在引力作用下的运动，从而完成模拟。而产生的最终粒子分布可再现宇宙的大尺度结构。例如，这些粒子可以反映当今星系和星系团的分布状况。

在分析这些结构的形成和演化之前，需要回答关于宇宙的一些基本问题。例如，宇宙中有多少物质？宇宙膨胀的速度有多快？驱动宇宙膨胀的暗物质和暗能量的性质是什么？

现代宇宙学测绘使用最强大的望远镜在最广阔的天空区域范围内观测，并追溯到数十亿年前，最终绘制出这些结构。将 N 体模拟得出的预测与这些测绘的结果进行匹配，有助于我们回答上述基本问题，进而增进我们对宇宙的诞生和演化的理解。

TensorFlow 宇宙 N 体解算器：FlowPM

数十年来，N 体模拟一直是宇宙学界的主要工具。受益于机器学习和统计推断领域的最新发展，我们引入了 FlowPM，宇宙 N 体模拟的纯 TensorFlow 实现。我们提供 Google Colab notebook 来进行此类模拟实验。备注：目前，我们的代码使用 TF1 编写而成（未来我们会将研究更新至 TF2）。

• FlowPM
  https://github.com/modichirag/flowpm

• Google Colab notebook
  https://colab.research.google.com/drive/1zc1nvra1HF01mTtpOlRigj-UBVzYgFqq#scrollTo=pvtJPFS3LfYv

设置好模拟参数（如框长和网格大小）后，执行模拟的代码片段将非常简单，并已包含在下文的完整代码中。此代码片段将生成观测到的大尺度结构，如图 2 所示。

# Generate Gaussian initial conditions for the matter distribution
initial_conditions = flowpm.linear_field(N,  L, ipklin, batch_size=batch)
# Sample particles, i.e. generate the initial displacement and velocity
state = flowpm.lpt_init(initial_conditions, a0=a0)
# Evolve particles from initial state down to present time with N-Body simulations
final_state = flowpm.nbody(state, stages, N)
# Visualize final density field i.e interpolate the particles to a grid
Final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions), final_state[0])
# Execute the graph!
with tf.Session() as sess:
    ic, istate, fstate, sim = sess.run([initial_conditions, state, final_state, final_field])

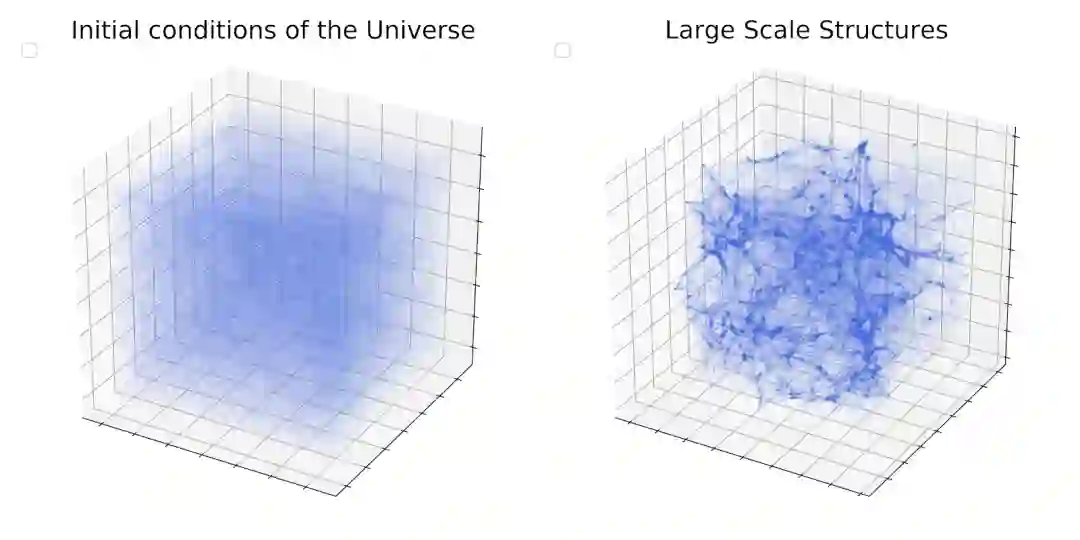
图 2：（左）N 体模拟开始时，物质在宇宙中的初始分布。（右）模拟最终快照中的物质最终分布。图上清晰可见具有塌缩暗晕、长纤维和空洞的大尺度结构

那么，在 TensorFlow 中进行此类模拟有哪些好处？该框架的优点主要可分为两大类：

1.分析和推理：TensorFlow 中的模拟具有宇宙学家以前没有使用的特性 — 可微分性。该功能为科学家开启了全新分析工具的大门，例如，开发基于模拟的高效推理技术。此外，通过此功能，我们还能够量化针对各种输入参数的最终观测结果响应。在我们位于伯克利宇宙物理中心（BCCP，加州大学伯克利分校）的研究小组中，我们很希望根据目前观测到的大尺度结构来进行反推 (时光倒流) 并重建初始条件[4] 。这就涉及到需要解决数 百万 个维度中的高度非线性优化问题，这只有使用具备可微分性的模拟（如 FlowPM）才能实现。下方视频是此重建的图示。

• 伯克利宇宙物理中心
  http://bccp.berkeley.edu/

所示为从最终暗物质宇宙场（右）中的大尺度结构重建宇宙初始条件（左）的动态

2.混合物理/深度学习模拟：该模拟支持开发混合前向模型，在该模型中，我们可将深度学习组件用作 N 体模拟的一部分。在现有计算资源条件下，无法对所有组件进行高精度模拟。根据科学研究目标的不同，当前模拟通常会在不同要素之间进行取舍：如在宇宙中观测到的各种长度尺度，观测到的星系质量范围，以及形成这些星系的各种物理过程。

但是，现在，针对具体的科学要求，我们可以使用深度学习替代模型，通过与基础 N 体模拟自然对接的方式纳入这些元素，进而在这种取舍之上做出改进。我们位于 BCCP 的小组开发的此类混合模拟示例[3] 如图 3 所示。假设我们要模拟宇宙中的气体动量密度。这些可观察量当前使用代价高昂的水力模拟进行模拟，但现在可改用 FlowPM 端到端模型来生成模拟结果，成本为原来的 1/1000。

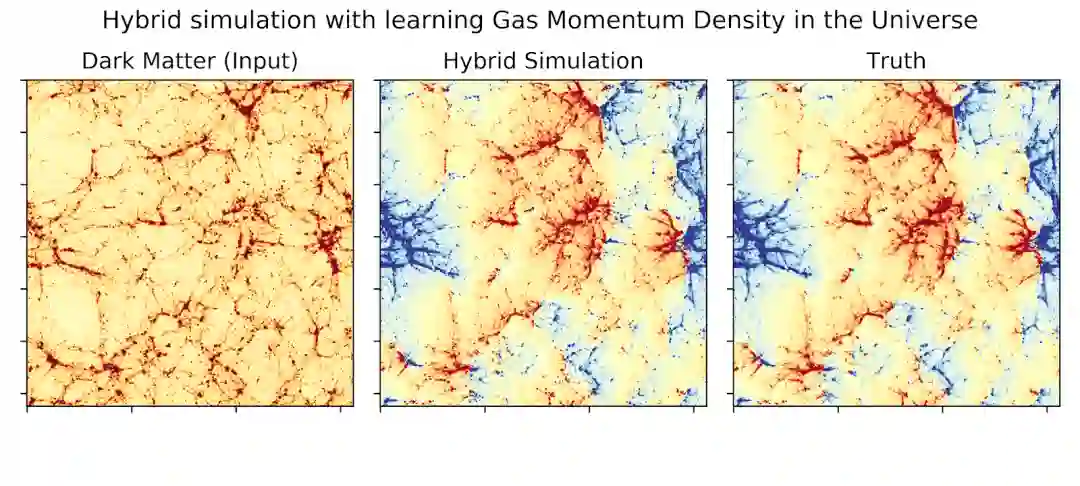
图 3：混合模拟示例，其中我们用 2 层非线性变换（网络）来补充 PM 模拟的暗物质输出（左），以模拟宇宙中的气体动量密度（中心）。将其与使用成本高达 1000 倍的水力模拟（右）所模拟的真实结果进行对比

使用 Mesh TensorFlow 进行分布式模拟

所有这些模拟的原理看起来都很简单，但是我们还面临另一个挑战；我们的宇宙 浩瀚无边！为准确匹配当前和将来测绘的观测结果，我们将需要同时模拟数十亿个粒子的演化。这给 N 体宇宙学模拟带来两种挑战：

1.持续模拟数十亿个粒子的演化在计算上代价高昂。另外，要估算所有粒子之间的重力，我们将需要在模拟中计算所有粒子对。这使得计算量按 N² 级的规模增长，因此也无法实现。幸运的是，还有一些近似算法让计算易于驾驭。我们在 FlowPM 中采用的一种算法是 Particle-Mesh (PM) 方法。在 PM 方法中，为估计重力，我们在大小为 N_g 的规则网格上离散空间，然后使用高度优化的 3D 快速傅立叶变换计算整个空间上的力。这可使计算成本从 N^2_g 减少至 N_glog(N_g)。

2.尽管对这些算法进行了优化，但数十亿个粒子也会让这些模拟非常占用内存。因此，需要网格至少为 1024x1024x1024 的有效尺寸的模拟无法在单个 GPU 上显示。因此，我们需要 模型并行 框架以开发大尺寸模拟，而这正是 Mesh TensorFlow 的用武之地。

• Mesh TensorFlow 
  https://github.com/tensorflow/mesh

Mesh TensorFlow 框架让我们能轻松地用分布式张量描述模拟，并在幕后持续跟踪设备间的分布式梯度和内存通信。通过在 Mesh TensorFlow 中编写 N 体解算器，我们可以将这些超级计算机上的庞大模拟量分布在多台设备之间。在此种模拟中，每个处理和网格组件在每个时间步下都会演化出不同的空间区域。使用相同的模拟代码，我们可以同时在云 TPU 上演化 128 个网格尺寸为 128x128x128 的独立宇宙，或者在 NERSC 等国家计算机设施的 64 个 GPU 上演化单个网格尺寸为 1024x1024x1024 的宇宙。除支持大型模拟之外，模型并行框架还允许我们通过在多个处理器之间分配计算来加速中间尺寸的模拟。如下方图 4 所示，我们可以看到，FlowPM 模拟的平均速度是当前可微分 python 模拟 FastPM 的 40 倍。

• N 体解算器
  https://github.com/modichirag/flowpm/tree/mesh

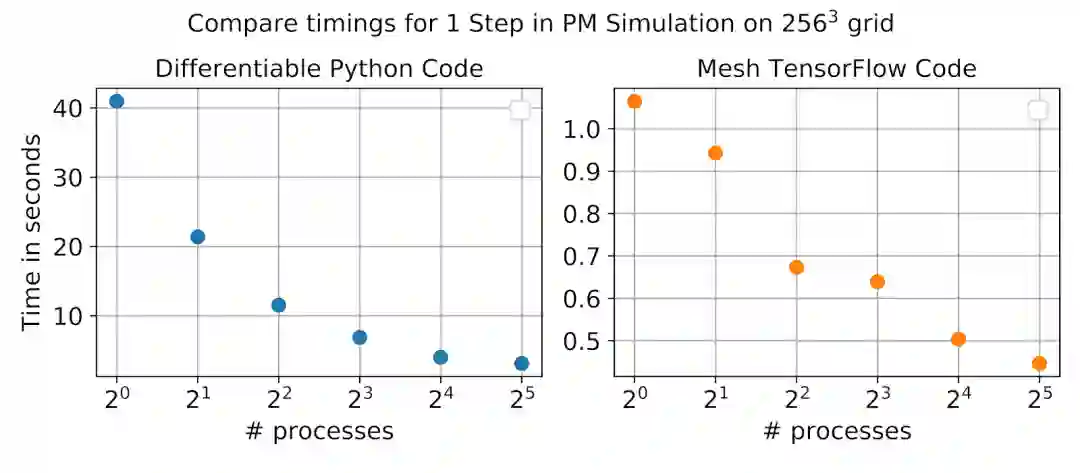
图 4：我们在 FastPM（在 Cori Haswell 内核上运行的基于 CPU 的 python 代码）和 FlowPM（在 Cori GPU 上运行的基于 GPU 的 Mesh TensorFlow 代码）的 2563 网格 PM 模拟中，将时间缩放与处理器数量进行 1 个时间步的比较

展望

三十多年来，我们的宇宙数值模拟已成为大尺度结构宇宙学的骨干技术。借助 FlowPM，我们正在迈出第一步，将此类模拟与深度学习组件集成到一个统一框架内，同时保持对基本现象的精准物理认知。在宇宙学中，这两者的结合为开发全新分析工具以及在迄今难以解决的领域中实现建模开启大门。这些是活跃的研究领域，随着新一代宇宙学测绘的临近而变得越来越紧迫，因为届时需要观测在十年交替时宇宙中即将显现的上千万个物体。借助 Mesh TensorFlow 的模型并行框架，物理建模和机器学习相结合的可能性变大，并且我们希望使用 FlowPM 开发的组件分析和计算工具也能使使宇宙学以外的其他学科的大尺寸科学应用受益。

我们衷心感谢 NERSC 的同事 Wahid Bhimj、Steve Farrell、Peter Harrington、Prabhat 和 Google 的 Niki Parmar、Thiru Palanisamy、Noam Shazeer、Youlong Cheng、Zak Stone 以及其他人士给予的支持，你们指引我们获得相关资源、积极讨论优化和改进此类模拟的方法，并提供有效的反馈。

参考文献

• [1] FastPM（FlowPM 的 基础 PM 方法）
  https://arxiv.org/abs/1603.00476

• [2] TF 中的 FlowPM 代码
  https://github.com/modichirag/flowpm

• [3] Dai 等
  https://drive.google.com/open?id=0B7_TnnOHCrvBcWxHR2tVUkR2N0xDbHo3TUxyN2hZemtZSUJn

• [4] 用神经网络重建初始条件 
  https://arxiv.org/abs/1805.02247

• [5] Mesh Tensorflow
  https://github.com/tensorflow/mesh
  https://arxiv.org/abs/1811.02084

• [6] 带有 MeshTF 的并行 FlowPM 代码
  https://github.com/modichirag/flowpm/tree/mesh