​【NIPS2017】深度学习真的不需要理论指导了？图灵奖得主讲座无人问津，贝叶斯之父Judea Pearl落寞身影背后引人深思

---

  新智元转载  

来源：专知

【新智元导读】今天带来一个落寞的背影。最近NIPS 2017 "Test of Time"论文大奖获得者Ali Rahimi 在长滩现场的演讲中把机器学习称为“炼金术”（Alchemy）引起机器学习界的大讨论，不难理解深度学习理论的研究似乎真的陷入了尴尬的境地。与此同时，寂寞的背影，听者寥寥的会场，图灵奖得主同时也是贝叶斯之父 Judea Pearl 的报告似乎并没多少人关心。而报告的题目《机器学习的理论障碍》（Theoretical impediments to machine learning）正是关于Judea Pearl对机器学习特别是深度学习背后理论的思考。

NIPS 2017 "Test of Time"论文大奖获得者Ali Rahimi 在长滩现场的演讲中抱怨当前机器学习尤其是深度学习使用的很多方法缺少（理论）理解。而Lecun则回怼说：仅仅因为理论没有追赶上实践的水平，就批评整个机器学习社区使用「炼金术」，这种言论是危险的。

CMU大学教授，Petuum公司创始人Eric Xing则在看到这组图后表示：这是NIPS2017大会上一个让人难过的场景。成为一个单纯的“炼金术师”并不可耻，可耻的是并不努力从“炼金术师”学成“化学家”。 意思是仅仅反复的做工程实践并没有什么不对的，但是还应该想想背后的原理。（不想当将军的士兵不是好兵？）

图：Judea Pearl演讲的会场

Judea Pearl简介

Judea Pearl 曾获得2011年的图灵奖，奖励他在人工智能领域的基础性贡献，他提出概率和因果性推理演算法，彻底改变了人工智能最初基于规则和逻辑的方向。他主要的研究领域是概率图模型和因果推理，这是机器学习的基础问题。图灵奖通常颁给纯理论计算机学者，或者早期建立计算机架构或框架的学者。

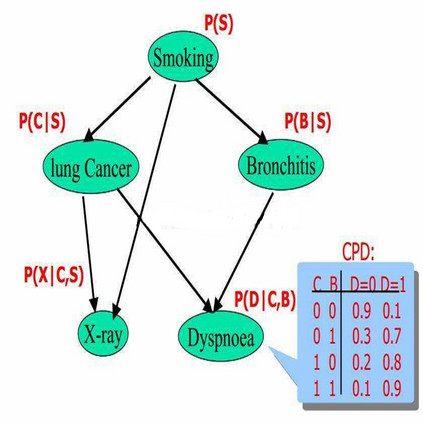
Judea Pearl 是 UCLA 计算机科学系的教授，他曾两次居于科学革命的中心：第一次是在 20 世纪 80 年代，他为人工智能引入了一套新的工具，叫贝叶斯网络。这种基于概率的机器推理模型使得机器能在复杂的、模糊的和不确定性的环境下工作。短短几年内，贝叶斯网络就完全替代了此前基于规则的人工智能方法。

第二次革命，鉴于贝叶斯网络在计算上的优势，Pearl 意识到简单的图模型和概率论（正如贝叶斯网络中的那样）也能用于因果关系的推理。这一发现为人工智能的发展奠定了另一个基础，但意义远非如此，这一能验证因果关系的、条理性的数学方法，几乎已经被所有科学和社会科学领域采用。

Judea Pearl 还是美国国家工程院院士，AAAI 和 IEEE Fellow，是以他儿子姓名命名的 Daniel Pearl 基金会的主席（他的儿子Daniel Pearl曾是华尔街日报记者，2002年被巴基斯坦恐怖份子绑架并斩首，为这事美国还专门拍了一部电影 ” A Mighty Heart” 。）

场外JudeaPearl亲自讲解自己的工作

http://web.cs.ucla.edu/~kaoru/theoretical-impediments.pdf

理论在深度学习中的作用

AliRahimi 阿里引起的理论之争一石激起千层浪，网络上出现了更多机器学习界的代表发声。今天芝加哥丰田研究院教授DavidMcAllester发表博文进行解读，以下内容为McAllester的观点：

这篇博文的主要受Ali Rahimi最近的NIPS演讲和Lecun回怼的启发。

• https://www.reddit.com/r/MachineLearning/comments/7hys85/nalirahimistalkatnipsnips2017testoftime/

• https://www.facebook.com/search/str/yann+lecun+alchemy/keywordssearch

这个研究话题从根本上就是理论和深度学习的关系。我将从Ali的演讲中摘抄一些引用。

• Rahimi：

机器学习已经成为炼金术。

炼金术是有效的（对于很多事情）。

但科学家已推翻二千年的炼金术的理论。

我想生活在一个社会，这个社会的制度建立在可证实的严谨的知识上，而不是炼金术上。

• LeCunn：

  理解（理论或其他）是一件好事。但是仅仅因为理论没有追赶上实践的水平，就批评整个机器学习社区使用「炼金术」，这种言论是危险的。

  
  

  为什么危险？正是这种态度使机器学习社区放弃神经网络 10 年有余，尽管大量实证研究证明神经网络在很多情况下非常有效。

我从根本上同意Yann的观点，他认为苛刻的要求会误导一个领域。也许最危险的是要用成熟的数学理论来打动同行，而不是寻求真正的进步。

但我想在这场辩论中加入我自己的观点。我将再次引用Rahini:

• Rahini：

  当一个深度网络不起作用时，我认为它是梯度下降的错误。

  梯度下降是深度学习的基石。梯度下降是局部搜索的一种形式。以下是一些局部搜索的例子:

  
  

  内燃机从十九世纪九十年代到二十世纪的演变。

摩尔定律指导下近50年来半导体工艺的发展。

包括人类大脑进化的生物进化。

从希腊数学到现代数学的演变。

Alphago zero训练时间，通过自我下棋成为世界上最强大的国际象棋程序。

局部搜索确实是神秘的。但是，我们真的能期待一个严格的局部搜索理论来预测或解释人脑的进化或数学知识的历史演变吗？我们真的可以期待通过某种梯度下降的二阶分析来预测未来二十年将出现哪些数学理论？我的立场是，局部搜索（梯度下降）是非常强大的，从根本上超出了任何完全严格的理解。

如今的计算能力已经达到了这样的水平：强大GPU加上强大架构设计上的梯度下降只能被理解为某种形式的非常强大的通用非凸局部搜索，其性质类似于上述例子。是的，特定的神经网络训练失败是梯度下降（局部搜索）的失败。但是那个观察提供提供的信息很少。

一个相关的问题是在通用人工智能（AGI）中时间帧上的方位。严谨是否有助于实现AGI？ 也许即使是Rahini也会发现对AGI的严格处理是不可能的。一个严谨者的普遍反应是，AGI太远太扯淡。但是，我觉得我们离得很近，这更让人兴奋。

我写了一篇关于关于近期的机器感知的合理性的博客文章（https://machinethoughts.wordpress.com/2017/07/22/the-plausibility-of-near-term-machine-sentience/）。

我相信洞察结构是可能的，而这种洞察可以成功地指导设计。LSTMs出现在1997年，因为有克服梯度小时的一种“理论洞察力”。理解批量标准化是克服内部协变量转换的一种方法，我确实认为我是在直观的层面来理解（我很乐意解释它）。直觉的非严格的理解是理论理解的基础。

20多年前，Fernando Pereira（可能他是引用别人）对我说“探险家”和“定居者”。探险者首先看到地形（没有严谨），定居者清理它（严谨）。考虑微积分或傅立叶分析。但在局部搜索的情况下，我不认为定理（定居者）将会解决它。

在我看来，一般局部搜索（AGI）的进展将来自寻找正确的计算模型——正确的通用架构——用于定义“强”局部搜索空间的结构。我已经写了一篇关于搜索一般认知架构的博文（https://machinethoughts.wordpress.com/2016/06/20/cognitive-architectures/）。

输或赢，我个人打算继续追求AGI。

参考文献：

https://machinethoughts.wordpress.com/2017/12/08/the-role-of-theory-in-deep-learning/

特别提示-贝叶斯之父 Judea Pearl Theoretical Impediments to Machine Learning 论文下载：请关注专知公众号，后台回复“TIML” 就可以获取论文pdf下载链接~

本文经授权转载自专知：Quan_Zhuanzhi，点击“阅读原文”可查阅原文。

---