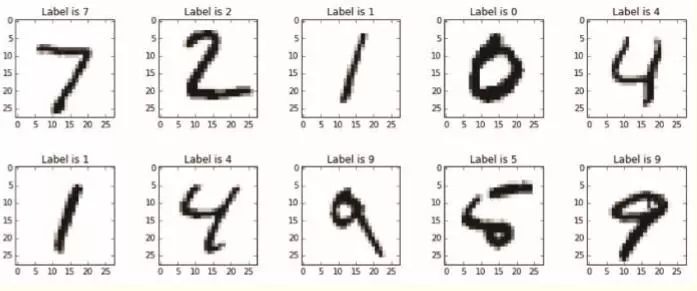
Python神经网络是这样识别手写字符哒？

当谷歌的AlphaGo战胜了人类顶级棋手，人工智能开始更多进入大众视野。而谷歌AI教父认为：“AlphaGo有直觉神经网络已接近大脑”。

千百年来，人类试图了解智能的机制，并将它复制到思维机器上。而从不满足于让机械或电子设备帮助做一些简单的任务，例如，使用燧石打火，使用滑轮吊起沉重的岩石，使用计算器做算术。

相反，我们希望能够自动化执行更具有挑战性、相对复杂的任务，如对相似的照片进行分组、从健康细胞中识别出病变细胞，甚至是来一盘优雅的国际象棋博弈。这些任务似乎需要人类的智能才能完成，或至少需要人类思维中的某种更深层次、更神秘的能力来完成，而在诸如计算器这样简单的机器中是找不到这种能力的。

具有类似人类智能的机器是一个如此诱人且强大的想法，我们的文化对它充满了幻想和恐惧，如斯坦利·库布里克导演的《2001: A Space Odyssey》中的HAL 9000（拥有巨大的能力却最终给人类带来了威胁）、动作片中疯狂的“终结者（Terminator）”机器人以及电视剧《Knight Rider》中具有冷静个性的话匣子KITT汽车。

1997年，国际象棋卫冕世界冠军、国际象棋特级大师加里·卡斯帕罗夫被IBM“深蓝”计算机击败，我们在庆祝这一历史性成就的同时，也担心机器智能的潜力。

我们如此渴望智能机器，以至于一些人受到了诱惑，使用欺骗手段，例如，臭名昭著的国际象棋机器Turkey仅仅是使用一个人隐藏在机柜内而已！

在20世纪50年代，人工智能这门学科正式成立，此时，人类雄心勃勃，对人工智能抱着非常乐观的态度。最初的成功，让人们看到了计算机可以进行简单的博弈、证明定理，因此，一些人相信，在十年左右的时间内，人类级别的人工智能将会出现。

但是，实践证明：发展人工智能困难重重，进展一度停滞不前。20世纪70年代，人们在学术界挑战人工智能的雄心遭到了毁灭性的打击。接下来，人们削减了人工智能研究经费，对人工智能的兴趣消失殆尽。机器那冰冷的逻辑，绝对的1和0，看起来似乎永远不能够实现细致入微的、有机的，有时甚至模糊的生物大脑思维过程。

在一段时间内，人类未能独具匠心，百尺竿头，更进一步，将机器智能探索带出其既定轨迹。在此之后，研究人员灵光一现，尝试通过复制生物大脑工作的机制，来构建人工大脑？真正的大脑具有神经元，而不是逻辑门。真正人脑具有更优雅更有机的推理，而不是冰冷的、非黑即白的、绝对的传统算法。

蜜蜂或鸽子大脑的简单性与其能够执行复杂任务的巨大反差，这一点启发了科学家。就是这零点几克的大脑，看起来就能够做许多事情，如导航、适应风向、识别食物和捕食者、快速地决定是战斗还是逃跑。当今的计算机拥有大量的廉价资源，能够模仿和改进这些大脑吗？一只蜜蜂大约有950 000个神经元，今天的计算机，具有G比特和T比特的资源，能够表现得比蜜蜂更优秀吗？

但是，如果使用传统的方法来求解问题，那么即使计算机拥有巨大的存储和超快的处理器，也无法实现鸟和蜜蜂使用相对微小的大脑所做的事情。受到仿生智能计算的驱动，神经网络（Netural Network）出现了，并且神经网络从此成为在人工智能领域中最强大、最有用的方法之一。

今天，谷歌的Deepmind以神经网络为基础，能够做一些非常奇妙的事情，如让计算机学习如何玩视频游戏，并且在人类历史上第一次在极其变化多端的围棋博弈中击败了世界级的大师。如今，神经网络已经成为了日常技术的核心，例如自动车牌号码识别、解码手写的邮政编码。

探讨的是神经网络，让你了解神经网络如何工作，帮你制作出自己的神经网络，训练神经网络来识别人类的手写字符。如果使用传统的方法来执行这个任务，那么将是非常困难的。

神经网络是如何实现的

计算机的核心部分就是计算器。这些计算器做算术非常快。对于执行与计算器相匹配的任务而言，如对数字进行相加算出销售 额、运用百分比算出税收、绘制现存数据的图表，这是很不错的。 

即使是在计算机上观看网络电视节目或听流媒体的音乐，也只涉及一 次又一次地执行简单的算术指令。在互联网上通过管道将 1 和 0 输送到计 算机，重建视频帧，所使用的算术也不会比你在中学所做的加法运算复杂，这一点也许令你颇为惊奇。 

计算机可以以相当快的速度，在1 秒钟内进行4 位数甚至10 位数的相加，这也许给人留下了深刻的印象，但是这不是人工智能。人类可能发 现自己很难快速地进行加法运算，然而进行加法运算的过程不需要太多的 智慧。简单说来，这只要求计算机拥有遵循基本指令的能力，而这正是计 算机内的电子器件所做的事情。

现在，让我们转到事情的背面，掀开计算机的底牌。 让我们观察下面的图片，看看你能认出图片中包含哪些内容。 你和我都看到了人脸、猫和树的图片，并识别出了这些内容。

事实上， 我们可以以非常高的精确度快速地做到这一点。在这方面，我们通常不会出错。 我们可以处理图像中所包含的相当大量的信息，并且可以成功地识别图像中有哪些内容。但这种任务对计算机而言，并不是那么容易，实际上，是相当 困难的。

我们怀疑图像识别需要人类智能，而这是机器所缺乏的。无论我 们造出的机器多么复杂和强大，它们依然不是人类。但是，由于计算 机速度非常快，并且不知疲倦，我们恰恰希望计算机能更好地进行求 解图像识别这类问题。人工智能所探讨的一切问题就是解决这种类 型的难题。 

当然，计算机将永远使用电子器件制造，因此研究人工智能的任务就 是找到新方法或新算法，使用新的工作方式，尝试求解这类相对困难的问 题。即使计算机不能完美地解决这些问题，但是我们只要求计算机足够出 色，给人们留下一种印象，让人觉得这是智能在起作用。

一台简单的预测机

让我们先从构建超级简单的机器开始。 想象一下，一台基本的机器，接受了一个问题，做了一些“思考”， 并输出了一个答案。与我们在上面的例子中进行的操作一样，我们从眼睛 输入图片，使用大脑分析场景，并得出在场景中有哪些物体的结论。 

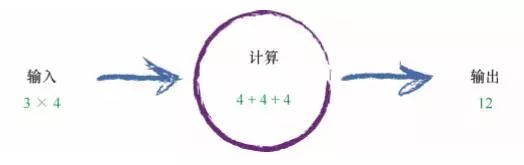
下面就是这台机器看起来的样子。

记住，计算机不是真的思考，它们只是得到包装的计算器，因此让我 们使用更恰当的词语来形容这个过程。

一台计算机接受了一些输入，执行了一些计算，然后弹出输出。下 列的内容详细说明了这一点。一台计算机对“3×4”的输入进行处理， 这种处理也许是将乘法运算转化为相对简单的一组加法，然后弹出答案 “12”。

你可能会想“这也没什么了不起的吧！”，没关系。这里，我们使用 简单和熟悉的例子来引出此后我们将看到的更有趣的神经网络的概念。

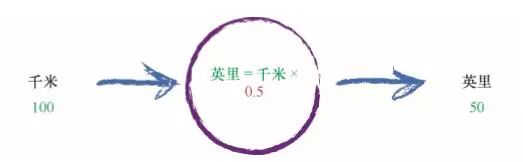
让我们稍微增加一点复杂度。 试想一下将千米转化为英里的一台机器，如下所示。

现在想象一下，我们不知道千米和英里之间的转换公式。我们所知道 的就是，两者之间的关系是线性的。这意味着，如果英里数加倍，那么表 示相同距离的千米数也是加倍的。这是非常直观的。如果这都不是真理， 那么这个宇宙就太让人匪夷所思了。 

千米和英里之间的这种线性关系，为我们提供了这种神秘计算的线索， 即它的形式应该是“英里 =千米 ×C”，其中 C为常数。现在，我们还不知道这个常数 C是多少。 

我们拥有的唯一其他的线索是，一些正确的千米/ 英里匹配的数 值对示例。这些示例就像用来验证科学理论的现实世界观察实验一样， 显示了世界的真实情况。

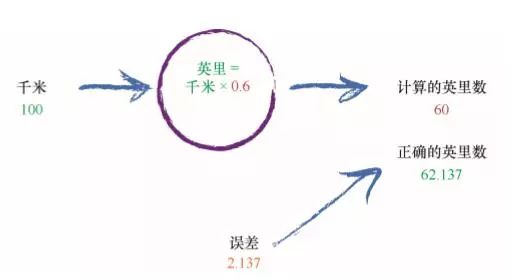
我们应该做些什么，才能计算出缺失的常数 C 呢？我们信手拈来一 个随机的数值，让机器试一试！让我们试着使用 C = 0.5，看看会发生什么情况。

这里，我们令：英里 =千米 ×C，其中千米为 100，当前，我们猜测 C为0.5。 

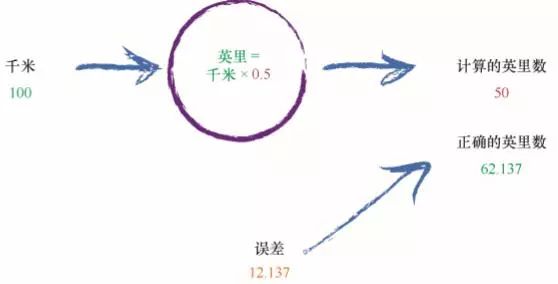
这台机器得到 50 英里的答案。 嗯，鉴于我们随机选择了 C = 0.5，这种表现还算不错。但是，编号为 2 的真实示例告诉我们，答案应该是 62.137，因此我们知道这是不准 确的。 我们少了 12.137。这是计算结果与我们列出的示例真实值之间的差值，是误差。即： 

误差值 = 真实值 - 计算值 　　　

 = 62.137-50 　　

= 12.137

下一步，我们将做些什么呢？我们知道错了，并且知道差了多少。我 们无需对这种误差感到失望，我们可以使用这个误差，指导我们得到第二 个、更好的 C的猜测值。 

再看看这个误差值。我们少了12.137。由于千米转换为英里的公式 是线性的，即英里= 千米 ×C，因此我们知道，增加C 就可以增加 输出。 

让我们将 C 从 0.5 稍微增加到 0.6，观察会发生什么情况。 现在，由于将 C 设置为 0.6，我们得到了英里 = 千米 ×C = 100×0.6 = 60，这个答案比先前 50 的答案更好。我们取得了明显的进步。 

现在，误差值变得更小了，为2.137。这个数值甚至可能是我们很乐 于接受的一个误差值。

这里，很重要的一点是，我们使用误差值的大小指导如何改变C 的 值。我们希望输出值从 50 增大一些，因此我们稍微增加了 C 的值。 

我们不必尝试使用代数法计算出 C需要改变的确切量，让我们继续使用 这种方法改进 C值。如果你还不能被我说服，还是认为计算出确切的答案才 够简单，那么，请记住，更多有趣的问题是没有一个简单的数学公式将输出 和输入关联起来的。这就是我们需要诸如神经网络这样相对成熟而复杂的方 法的原因。 

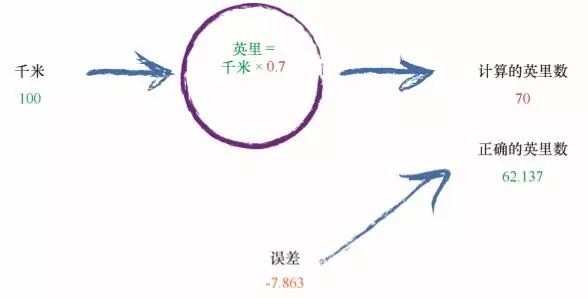
让我们再次重复这个过程。输出值 60 还是太小了。我们再次微调 C， 将其从 0.6 调到 0.7。

糟糕！过犹不及，结果超过了已知的正确答案。先前的误差值为 2.137，现在的误差值为 -7.863。这个负号告诉我们，我们不是不足，而是超调了。请记住上面的公式，误差值等于真实值减去计算值。 

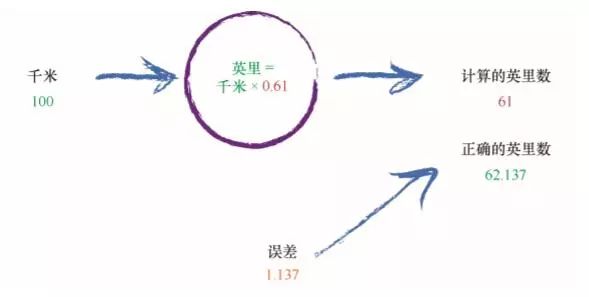
如此说来，C = 0.6 比 C = 0.7 好得多。我们可以就此结束这个练习，欣然接受C = 0.6 带来的小小误差。但是，让我继续向前走一小段距离。 我们为什么不使用一个较小的量，微调 C，将 C 从 0.6 调到 0.61 呢？

这比先前得到的答案要好得多。我们得到输出值 61，比起正确答案 62.137，这只差了 1.137。

因此，最后的这次尝试告诉我们，应该适度调整 C 值。如果输出 值越来越接近正确答案，即误差值越来越小，那么我们就不要做那 么大的调整。使用这种方式，我们就可以避免像先前那样得到超调的 结果。

 

同样，读者无需为如何使用确切的方式算出 C 值而分心，请继续关注 这种持续细化误差值的想法，我们建议将修正值取为误差值的百分比。直 觉上，这是正确的：大误差意味着需要大的修正值，小误差意味着我们只 需要小小地微调 C 的值。 

无论你是否相信，我们刚刚所做的，就是走马观花地浏览了一遍神 经网络中学习的核心过程。我们训练机器，使其输出值越来越接近正确的 答案。

这值得读者停下来，思考一下这种方法，我们并未像在学校里求解数 学和科学问题时所做的一样一步到位，精确求解问题。相反，我们尝试得 到一个答案，并多次改进答案，这是一种非常不同的方法。一些人将这种 方法称为迭代，意思是持续地、一点一点地改进答案。

分类器与预测器并无太大差别

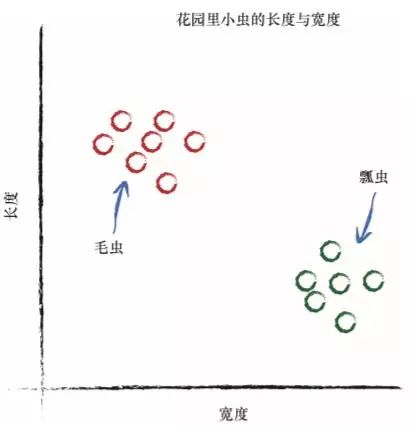
因为上述的简单机器接受了一个输入，并做出应有的预测，输出结 果，所以我们将其称为预测器。我们根据结果与已知真实示例进行比较所 得到的误差，调整内部参数，使预测更加精确。 现在，我们来看看测量得到的花园中小虫子的宽度和长度。

在上图中，你可以清楚地看到两群小虫。毛虫细而长，瓢虫宽而短。 你还记得给定千米数，预测器试图找出正确的英里数这个示例 吗？这台预测器的核心有一个可调节的线性函数。当你绘制输入输 出的关系图时，线性函数输出的是直线。可调参数Ｃ改变了直线的 斜率。 

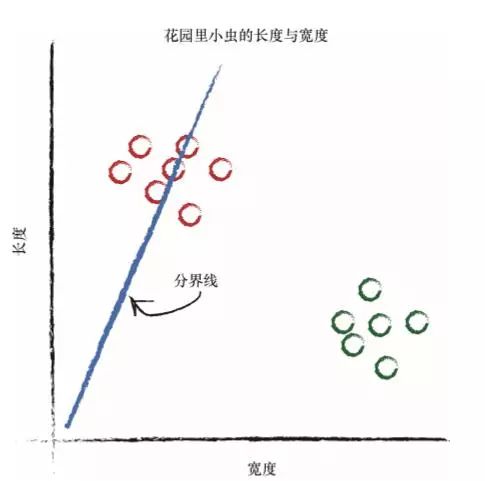
如果我们在这幅图上画上一条直线，会发生什么情况呢？ 虽然我们不能使用先前将千米数转换成英里数时的同样方式，但是我们也许可以使用直线将不同性质的事物分开。

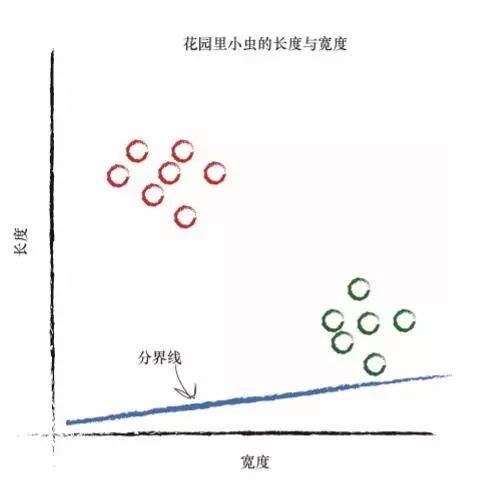
在上图中，如果直线可以将毛虫与瓢虫划分开来，那么这条直线就可 以根据测量值对未知小虫进行分类。由于有一半的毛虫与瓢虫在分界线的 同一侧，因此上述的直线并没有做到这一点。 让我们再次调整斜率，尝试不同的直线，看看会发生什么情况。 这一次，这条直线真是一无是处！它根本没有将两种小虫区分开来。 让我们再试一次：

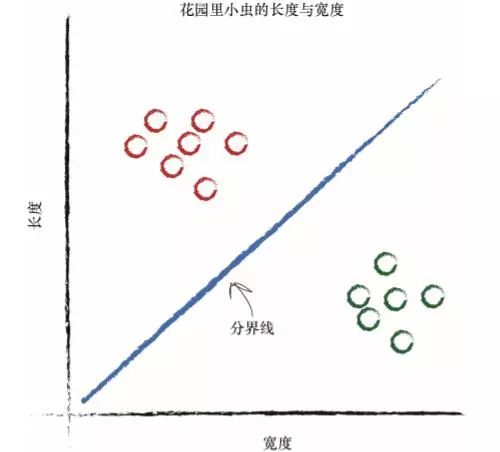
这条直线好多了！这条直线整齐地将瓢虫与毛虫区分开来了。现在， 我们可以用这条直线作为小虫的分类器。 我们假设没有未经发现的其他类型的小虫，现在来说，这样假设是没有问题的，因为我们只是希望说明构建一台简单的分类器的思路。 

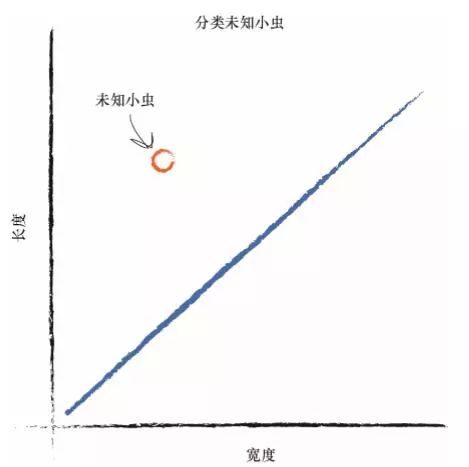
设想一下，下一次，计算机使用机器手臂抓起一只新的小虫，测量其宽 度和长度，然后它可以使用上面的分界线，将小虫正确归类为毛虫或瓢虫。 看看下图，你可以看到未知的小虫位于直线之上，因此这是一条毛 虫。这种分类非常简单，但是非常强大！

我们已经看到了，在简单的预测器中，如何使用线性函数对先前未知 的数据进行分类。 但是，我们忽略了一个至关重要的因素。我们如何得到正确的斜率 呢？我们如何改进不能很好划分这两种小虫的分界线呢？ 这个问题的答案处于神经网络学习的核心地带。

∑编辑 | Gemini

选自 | 异步图书

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域

经采用我们将奉上稿酬。

投稿邮箱：math_alg@163.com