郑文琛：基于网络功能模块的图特征学习 | AI 研习社79期大讲堂

2018 年 11 月 4 日 AI科技评论

AI研习社按：图是一种常见的数据结构，可以被用于许多不同的预测任务。如何从图数据学习有效特征是个重要的问题。我们的新概念是从点和边出发，拓展到更高阶的子图结构（比如路径、子图）来帮助图特征学习。这些高阶的子图结构通常具有不同的功能，事实上在一起共同构造了整个网络，所以我们称这些高阶的子图结构为网络功能模块（Network Functional Blocks）。

在这次分享中，嘉宾将用语义相关度搜索（Semantic Proximity Search）作为一个应用例子，来介绍他们最近在探索不同粒度的网络功能模块、以进行有效图特征学习的一些进展。

分享嘉宾：

郑文琛，微众银行人工智能项目组专家工程师和副总经理。主要研究方向为结构化数据的特征学习和迁移学习，已在相关研究领域发表了60余篇顶级会议和期刊论文，并拥有多项专利和技术。

在图数据特征工程的成就获得国际人工智能顶级会议 IJCAI 2018 年的 Early Career Spotlight，在迁移学习应用于用户行为识别的成就获得国际会议ICCSE 2018年的最佳论文奖。是 Cognitive Computation 杂志的副主编。同时也是多个顶级人工智能国际会议的编委会委员和研讨会的组织者。

公开课回放地址：

http://www.mooc.ai/open/course/560?=Leiphone

分享主题：基于网络功能模块的图特征学习

分享提纲：

图特征学习简介。
网络功能模块的概念，及其在语义相关度搜索的应用。
利用节点路径作为网络功能模块的解决方案。
利用子图扩展路径作为网络功能模块的解决方案。
利用异质有向无环图作为网络功能模块的解决方案。
总结。
微众 AI 招聘简介

AI 研习社将其分享内容整理如下：

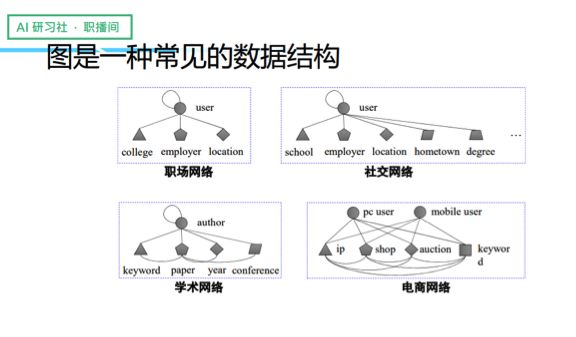
首先，我给大家做一些简单的介绍，图是一种常见的数据结构，我们会发现存在很多不一样的图结构，尤其是这种异质图的网络，比较常见的类型包括职场网络、社交网络、学术网络和电商网络等等。

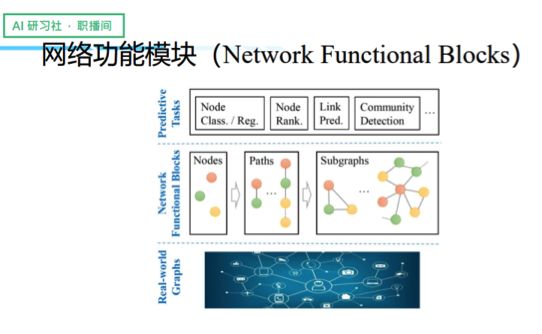
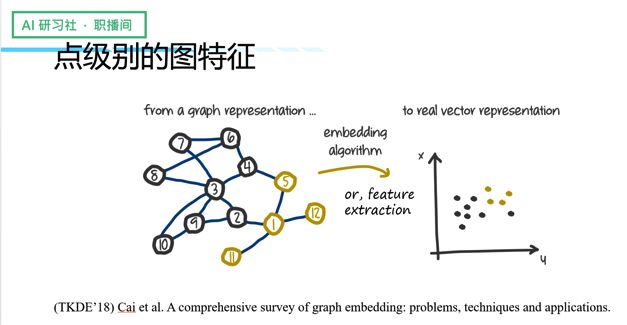
过去我们处理图数据/图的特征学习，主要解决的是「点」层面的图的特征学习，比如下面这张图，左边是图的结构，我们通常会据此做图的特征学习，就是将图上的每个点映射到第一维的空间上，这样做的话图上相近的点在第一维空间上同样会很靠近，黄色的点与黄色的点聚在一起，黑色的点与黑色的点聚在一起。

将一个图的结构映射到一个低维空间，从而得到一个点的表征，是一种比较简单的做法。实际上，图的结构还挺有意思的，特别是当图存在异质信息的时候。由于图本身具有拓扑结构，我们会发现存在很多不同的模块。考虑一个电商图，这个点可能是个买家，而在功能定位上它是一个角色（role）。除了点的结构以外，还存在其他的一些结构，比如说路径（买家-车-卖家），更复杂的我们还有子图（卖家-书&城市-买家）。

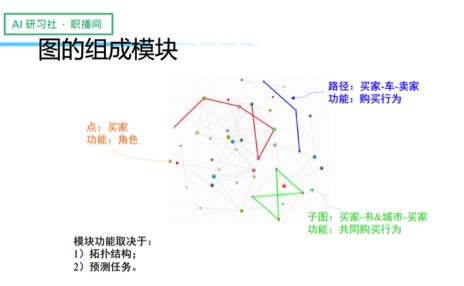
因此，同样的一张图，通过不同的点、不同的图来组成模块，它们之间是有区别的，从点——路径——子图，它们各自承载不同的功能，正因为功能的不同，随之语义也就不同。所以我们认为一张图是由许多不同的模块组成的，而每一个模块的功能主要取决于两个因素：一是拓扑结构，也就是说形状是什么样的；二是它的预测任务究竟是什么。

这也意味着，图并不只是点与点之间的连接，实际上这些点与点之间的变化是很丰富的，它们构成了不同子图的结构，这些子图结构又为我们带来了丰富的语义。

根据传统的做法，大家会直接把图上的点单独做成特征向量，那么问题来了，我们能不能利用好这些含有丰富语义的拓扑结构，无论是路径也好，子图也好，我们将它们扩展开来，利用语义更丰富的这些结构作为网络的功能模块，再基于这些功能模块来做网络特征学习，最后利用这些特征来做点的分类、回归、排序等等。总之，不局限于点的层面，而是探索网络功能模块这么一个概念。这是我们的一个整体思路。

语义相关度搜索（Semantic Proximity Search）

我们近期在做的工作，是探索一些比较特殊的网络功能模块的使用场景。这里我会以一个场景作为例子介绍这个网络功能模块的概念。这个例子就是语义相关度搜索（Semantic Proximity Search），这是一个比较常见的异质图搜索应用。在语义相关度搜索使用场景中，只要给定一个 query 和一个 relation，可以对其他节点进行排序，让我们对这个应用有了很大的想象空间。再者，异质图本身存在不同的功能模块，用来做语义相关搜索可说是最适合不过。

那么做语义相关检索会遇到哪些挑战呢？我们认为主要有两个：

1）点嵌入（node embedding）是一个比较间接的解法。我们做语义相关度检索，关心的是两个节点之间的语义相关度，对于点嵌入来说，它更关心的是每个节点之间的向量。考虑到两个节点之间并不一定直接相邻的，在给定两个点的向量后，我们需要算出两个点之间的距离，这意味着必须通过很多种方式去计算，然而我们并不知道哪种计算方式是最好的。此外，在大部分情况下，点嵌入更多被用来处理同质图；如果是异质图，我举个例子：「我买了一个牙刷」，不能说我跟牙刷的 embedding 很像，这说明什么呢？传统的 node embedding 是很难处理这种图的异质性的。总而言之，node embedding 是一个比较间接的解法，因为关心的是两个点之间的结构，而不是单个点的结构。

2）有没有一些工作是专门做异质图嵌入的呢？有，比较常见的是知识图谱嵌入，目前这块有许多特别好的工作。我们认为知识图谱的 embedding 是非常有意思的解法，不过要强调的是，知识图谱其实是比较特殊的异质图，一般会分为 head、 relation、tail 几个部分，然而一般的异质图很少存在这么「干净」的关系链。如果考虑的是两个点之间的距离，那么我们关心的重点不是究竟哪个点先嵌入的，而是这两个点之间的结构的嵌入。

这是我们认为在工作上比较有挑战性的地方。

利用节点路径作为网络功能模块的解决方案

接下来我会介绍我们的三个工作——三种用于解决语义相关搜索任务的网络功能模块（Network Function Blocks）。

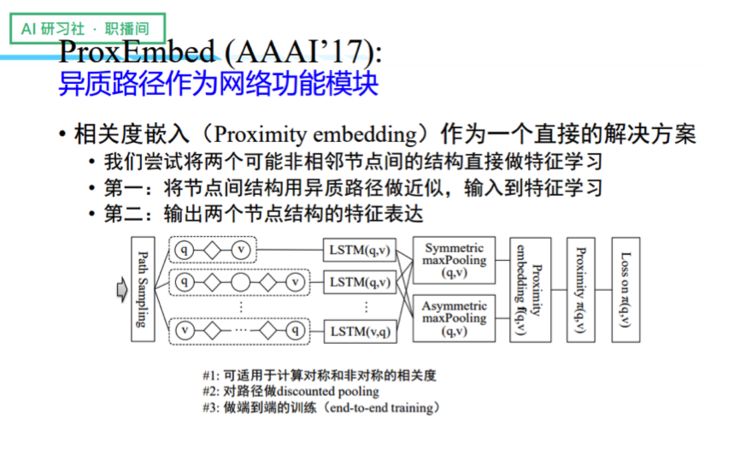
第一个工作很简单，我们利用异质路径作为网络功能模块，我们的主体思路是，既然关心两个节点之间的距离，那就干脆把两个点之间的网络结构做成输入，由此算出引向量特征，再综合算出相关度。这样做的好处是，一是把节点之间的结构变成一个映射，这是一种比较直接的做法；另外，由于这是一个异质子图结构，这种做法可以避免我们不停地去考虑每个节点的处境。

在具体的操作上，我们首先把两个节点之间的结构（通过异质路径获得）输入到特征学习里（可以采用任意序列的学习模型），接着做一些 discounted pooling，因为对于整个特征表达而言，有些路径可能很长，有些路径可能很短，有些路径则可能不是非常显著。结束后，我们将这些不同的路径整合成一个向量，最终得到一个 embedding，再将 embedding 乘以参数向量来得到最终的距离值。对于语义相关度搜索来说，只要给定点和点之间的距离，我们就可以做一个排序。这也是我们选择做一对一的训练和对路径做 discounted pooling 的原因，过程非常简单，结果却挺有意思的。

ProxEmbed 是一种基于路径的操作方法，事实上是通过一堆路径给两个节点之间的网络结构做近似。这样的 idea 也被利用到许多其他领域的工作里。这种 path-based 的方法尽管很成功，但我们后来发现路径是一种比较低阶的结构，如果对每个路径进行单独考虑，其实能够挖掘出来的信息是非常有限的，除非拥有非常优秀的 pooling 策略，不然你没法判断信息是如何被不同路径相互看到的，因此不一定足以描述丰富的语义。

利用子图扩展路径作为网络功能模块的解决方案

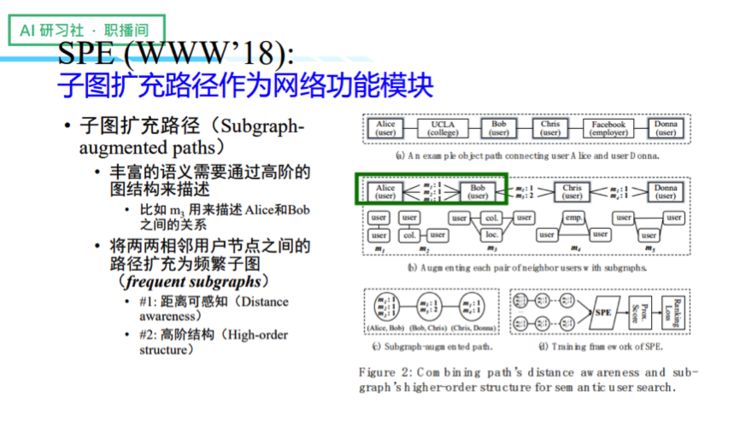
接着我们做了第二个工作，我们将路径做了扩展。刚刚我们有提到两个节点之间的关系不只有路径，还包括频繁子图，于是我们就在思考，有没有可能通过频繁子图去扩充路径的结构。为什么要做路径的扩充呢？因为点和点之间的路径能够很好地描述点和点之间的距离，如果再给点和点之间的关系增加一些丰富的子图语义信息，路径的表达能力将会因此大大增强。通过增加频繁子图的语义信息，我们最终可以得到 subgragh-augmented path，接着我们将它作为模型特征的学习，将 subgragh-augmented path 作为映射，从而学习到特征表达，最终算出它的语义距离（Proximity Score）。

可能有人会问，为什么在具体的操作上考虑的是用户和用户之间的关系，而不是任意两个点之间？原因是我们在提到语义相关搜索的时候，其实指的是和用户相关的语义相关搜索，这种应用考虑的更多还是用户和用户之间的关系，所以我们只对用户做两两交叉。另外，这种交叉还有一个好处，那就是可以减少计算的复杂度。

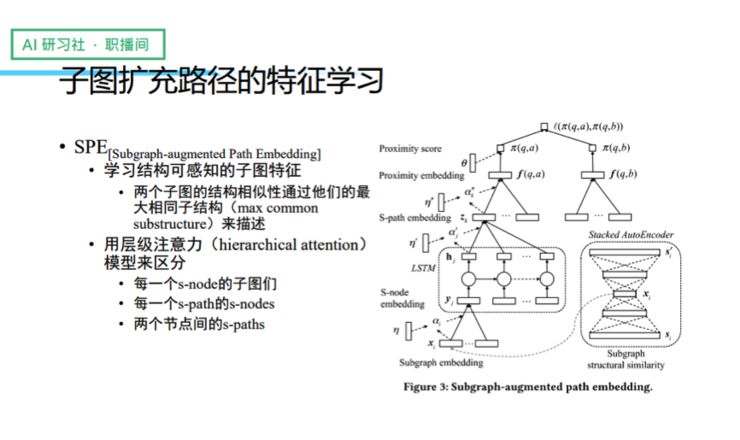
考虑到并不是所有子图、S-node、S-path 的贡献都是一样的，我们专门做了一个分层级注意力（hierarchical attention）模型来帮我们做筛选。此外，我们还考虑到子图路径其实是有结构的，所以专门针对子图的 embedding 结构的相似性，我们来描述两个节点之间的 embedding 关系，由此得到每一个节点和节点之间的 subgragh-augmented path 的一个全新 embedding。

我们的工作基于这么一个假设，那就是子图的 patterns 和 instances 都是预先算好的。在实际的操作中我们发现这个假设是可以被接受的，因为频繁子图经常会被离线算好，再用来作为图索引。我举几个比较典型的例子，比如阿里巴巴的反欺诈和 Twitter 的用户内容推荐，都是如此。另外，我们发现过往的一些工作中，也存在很多这种高效的子图挖掘和匹配的算法。

那么问题来了，我们能不能不做子图挖掘，然后将这些丰富的子图结构给利用起来呢？

利用异质有向无环图作为网络功能模块的解决方案

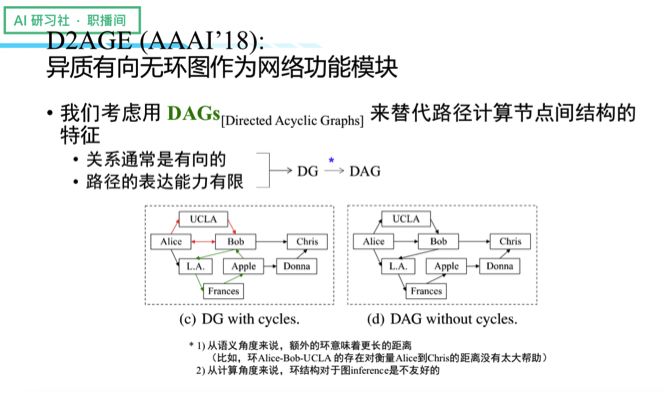
带着这个问题，我们又做了另外一项工作，那就是利用异质的有向无环图作为网络功能模块。我们使用 DAGs（Directed Acyclic Graphs）代替路径去计算节点结构的特征，主要是基于这么一项考虑：关系通常是有向的，然而路径的表达能力却有限。另外，DG 一般是环状结构，环则意味着更长的距离，对于描述两个点之间的关系并没有多大好处。况且从计算角度来说，环结构对于图的 inference 是不友好的。于是我们将部分的环去掉，最终得到 DAG 结构。

接下来，我们需要解决的是 DAGs 的产生效率问题，为此我们引入了一个距离可感知的 DAG 产生机制。我们会预先进行采样，采样好路径以后，我们将这些路径拼成一个图，然后利用路径遍历来构建 DG，过程中通过一套计算来进行去环，经过不停地遍历所有的 path 以后，我们最终可以得到 DAG 结构。这样处理的好处是，可以避免一个点到另一个点的结构只有一种 DAG。接着我们可以利用一堆 DAG 去给两个点之间的结构做近似，让语义变得更加丰富。

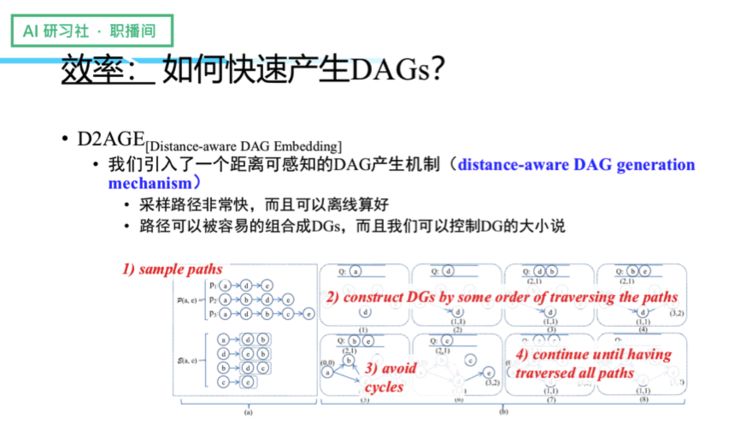
解决了 DAG 的产生效率问题，接下来我们要解决的是如何去描述和做特征学习，为此我们做了一个距离递减机制（recursive distance discount mechanism），因为我们发现点和点之间的结构路径的贡献率不一定都是一样的，这就凸显了距离的重要性。当我们仔细观察每一个 DAG 的结构时，每个节点都有不同的前驱。为了区分不同节点的迭代贡献率，我们可以根据不同前驱到达 query 的距离，将之与 predecessor 综合起来进行计算，来得到最终目标节点的 embedding，每个节点我们可以不停往后推，直至得到最终的 embedding 为止。

实验结果

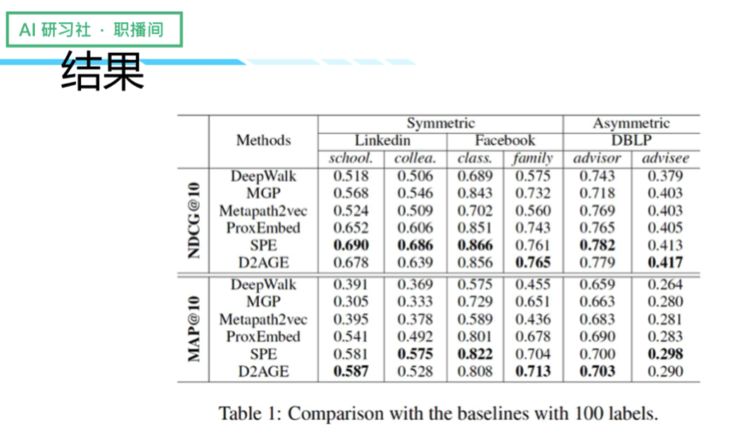
最后我们做了一些实验，主要测试三个数据集的六种语义关系，这些数据集包括了 LinkedIn、Facebook 和 DBLP。因为这是一项排序任务，因此我们加入了一些评估指标，那就是 NDCG（normalized discounted cumulative gain）和 Map（mean average precision）。

同时我们还列了一些比较典型的 Baseline 算法：首先是 deep walk ranking（DWR）算法，它从一个点采集一堆的路径，来学习节点特征；第二个是 meta-graph proximity（MGP），通过数任意两个节点间的 meta-graph 个数来计算节点间距离；第三个是 Metapath2vec，通过采样 metapaths 来学习节点特征。

最终结果显示，ProxEmbed、SPE 以及 D2AGE 三者在不同的 symmetric 和 asymmetric 里的效果都比较好，当中 SPE 的表现是最出色的，因为 SPE 为了在挖掘频繁子图方面做了较多工作，因此得到的信息更多更好。其次就是 D2AGE，效果跟 SPE 比较接近，有些地方甚至表现得更好，说明了即使不挖掘频繁子图，也有可能获得比较稳定的效果。

总结

最后我再总结以下我们的工作。我们主要想利用图特征学习来解决语义相关度检索任务，而我们认为点嵌入（node embedding）是一个间接的解决方案，所以我们提出把 query 和 target 之间的结构拿来做特征学习。具体要如何获得结构特征？我们采用的是 network functional blocks 方法，也就是三种基于网络功能模块的图特征学习方法。第一项工作是 ProxEmbed，利用异质路径作为网络功能模块；第二项工作是 SPE，利用子图扩充路径作为网络功能模块；第三项工作是 D2AGE，利用有向无环图作为网络功能模块。

最后这些模块都在数据集上取得了比 baselines 要好的效果。

我们整理了一份关于 network functional blocks 近期工作的文献集，同时我们也开源了我们所有的工作数据和代码，感兴趣的同学可以到网上去检索，然后自己做一些复现。