赠书 | 未来世界, 人类的生活不过是种种算法?

2017 年 11 月 23 日 遇见数学 遇见数学

TED教育视频: 《算法是什么?》

下文节选自《算法小时代》, 已获图灵许可, [遇见数学] 在此特别表示感谢! 文末有赠书活动, 欢迎关注!

什么是算法?

想理解什么是算法，我们要先设想一个场景。几千年前，一位祖先凭着他对已故祖母如何做面包的记忆，尝试自己做面包。但是，他真的不知道该怎么做。他犹豫着，一开始先将麦仁放入沸水中，然后对自己说，这也许是个糟糕的想法。这位祖先的困境，正是我们都会面临的情况——遇到某一个问题，却又不知道该如何解决。我们想着解决方法，去尝试，反复探索实验，顺便有了一点点意外发现，直至成功……或者失败。

然而，真正的面包师并不是这样做的。他们不会给每炉面包都重制一个烘焙食谱，因为他们已经掌握并牢记了面包的烘焙方法。多亏了面包食谱，面包师可以每天给我们提供面包。事实上，人类文明的发展不仅源于有些人的发明创造，也因为另有人“复制”了这些发明，才使其得以改进。但是，我们忘却了面包食谱的宝贵之处。首先，食谱降低了不确定性：多亏了它，面包师知道，除非突遭一场灾难，否则面包将会在晚餐时准备好。有了这个食谱，不需要什么想象力或是天赋，任何人都可以做面包。就拿两位作者来说，我们对面包烘焙没有任何天赋，但仍可以从网页上找到恰巴提的食谱，运用适当的和面力度，借助更富有想象力和才华的面包师们写下的方法，做出面包。最终，这个食谱成为了人类遗产中的一部分，在几千年的历史长河中，代代相传。

食谱就是一个算法，我们就此有了“算法”概念的初步定义：一个算法是解决一个问题的进程。我们并不需要每次都发明一个解决方案。

甜番茄 - 黑豆卷食谱

从这个定义不难看出，自人类历史初期，我们就一直在发明、使用和传播着各种各样的“算法”，用来烹饪、雕琢石器、钓鱼、种植扁豆及小麦，等等。

进程和符号

有些算法与面包食谱不同，它们能解决书写符号的问题，例如数字、字母等。算法汇集在一起，形成蕴含不同含义的数目、词语、句子及文本。

例如，二分查找算法的用途是在字典中搜索某个特定词。二分查找法从字典中间开始查找，对比目标词与中间词的位置，根据目标词位于中间词的前或后，来选择字典的前半部分或后半部分作为新字典，然后再用二分查找法继续查找，以此类推，直到找到目标词为止。这一算法解决涉及一种书写符号——字母的问题。还有一些算法可以实现加法、减法等，解决涉及另一种书写符号——数字的问题。这类算法被称为“符号算法”。

计算机科学家往往将“算法”一词的含义限定为此类“符号算法”。考虑到这种限制，自然，我们就不能将算法的历史追溯到文字发明之前了。然而，广义上的算法概念其实与文字同样古老。从迄今人类所发现的最古老的书面踪迹表明，古代书吏已经开始使用算法了，例如用于记账的加法和乘法。文字可能就是因此而发明的。

算法和数学

数学家们从很早便开始关注算法的设计了。比如，大约公元前300 年的欧几里得算法可以计算两个整数的最大公约数。我们简单说明一下。读者若是在攀登数学高峰时感到吃力，大可以直接跳过这一段，或把以下内容当作一首深奥的诗，尽量去理解。

一般来说，一个算法会在输入端接收数据，这些数据构成了算法的参数。在欧几里得算法中，输入数据就是两个不为零的整数，设为 a 和 b，且 a 大于 b，例如 a 等于 471，b 等于 90。通常，算法会在输出端返回另一些数据。在欧几里得算法中，输出数据是一个整数，即a 和b 的最大公约数。

将欧几里得算法应用在整数 471 和 90 上，即有：

用 90 和 21 替代 471 和 90，
然后用 21 和 6 替代，
接着用 6 和 3 替代，
再用 3 替代，这时 3 即为所求。

在上述例子中，算法的每一步都需要计算 a 除以 b 的余数 r，随后用被除数 b 替代除数 a，余数 r 替代被除数 b。因此，由 471=5×9 + 21 可知，471 除以 90 的余数为 21。在第一步中，第一个数 471 被 90 替代，而第二个数 90 则被余数 21 替代，以此类推。但有一个例外：当余数为 0时，就停止计算，且数 b 即为最终结果。这种情况出现在上述例子中的最后一步：我们用 6 除以 3，余数为 0，那么 3 即为所求。

算法也是中世纪西方数学家所关注的核心问题。数学家们引进了印度- 阿拉伯数字，以及与这种数字系统配套的算法。其中一本著作是通晓阿拉伯语的波斯数学家穆罕默德•穆萨•花拉子米在 9 世纪撰写的《印度计算法》（Algoritmi de numero indorum）一书。“花拉子米”（al-Khuwārizmī）一名源自作者的出生地花剌子模地区，今属乌兹别克斯坦。有文献证明，自1230 年起，花拉子米这个名字就成了“算法”（algorithm）一词的来源。

用语言来表达

算法会自然而然地运用到与数学有关的对象上。其实，人类的一切活动中都有算法的身影，算法概念涉及到方方面面。但我们要先解决一个关键问题：如何描述算法？

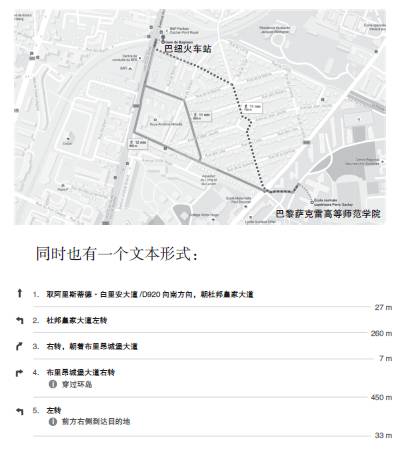
假设我们想从巴纽火车站到达位于卡尚镇的巴黎萨克雷高等师范学院。几十个学生和教师每天早上都走同一条道路：首先沿着杜邦皇家大道走，接着是布里昂城堡大道。在不知不觉中，他们可能就用到了算法——一种从火车站到校园的程序。

谷歌地图提供了这个算法的图形形式：　

如果我们给一个大学生解释这个算法，用一个简明扼要的方式就能表达清楚，但如果要给一个小孩子解释，就需要更详尽的细节。因此，讲解算法的方式是一个社会学问题，取决于谈话对象和谈话对象拥有的常识水平。

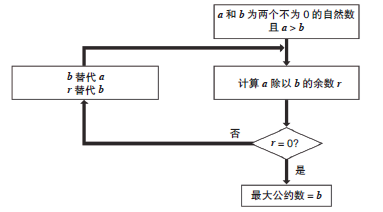
同样，欧几里得算法也可以用文字形式表达：

计算 a 除以 b 的余数 r，
当 r 不为 0 时，
用 b 替代 a，
用 r 替代 b，
继续计算 a 除以 b 的余数 r，
当余数 r 为 0 时，b 即为所求。

维基百科又提供了一种图形表达式：

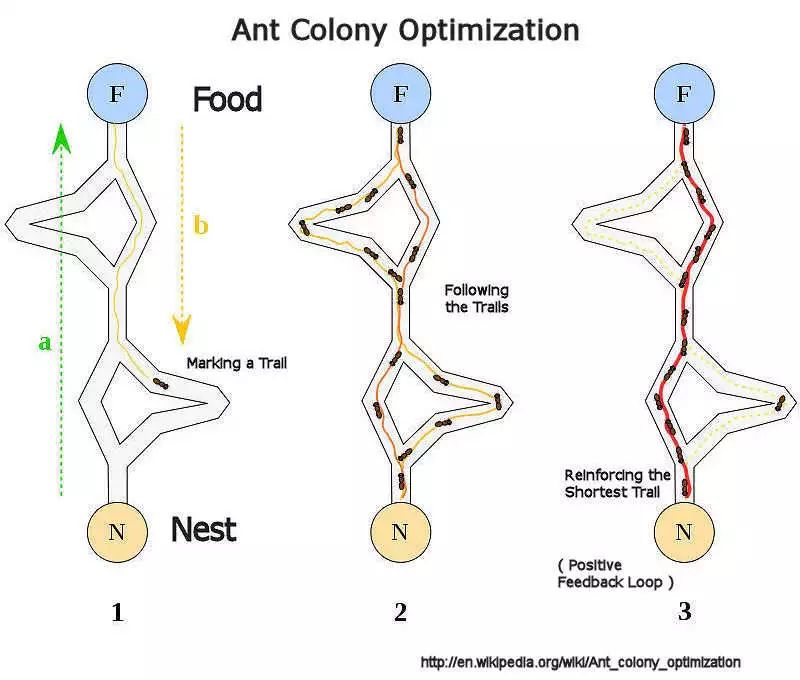
所以，一种算法可以有不同的语言表达形式。然而，有一种表达形式不依赖于语言。一名学生没睡醒就去了校园，走起路来晃晃荡荡，就像在梦游，他运行的这个随机算法没有任何语言表述。还有一个例子能更好地说明这一令人困惑的现象。蚂蚁寻找食物时，使用了非常复杂的算法，在空间里进行定向。侦察蚁开始随机浏览蚁穴四周。当其中一只蚂蚁发现食物的时候，便会在返回自己蚁群的一路上留下跟踪信息素。受到跟踪信息素的指引，其他路过此区域的蚂蚁会沿着这条路径前行。当蚂蚁带着食物返回蚁穴时，也会一路留下自己的跟踪信息素，以增强轨迹信息。

蚁群算法是一种用来在图中寻找优化路径的机率型算法

如果有两条路径都能到达同一个食物源，那么在同一时间内，沿最短路径行走的蚂蚁往返蚁穴与食物之间的次数将比沿着长路径走的蚂蚁更多。于是，前者也会留下更多的跟踪信息素。这时，最短路径的信息将会更强，也越来越具有吸引力。跟踪信息素是有挥发性的，如此一来，被冷落的最长路径最终会消失。

蚁群利用一个复杂的算法确定了最短路径。早在蚁学家用语言记下这种现象之前，蚂蚁就很好地运用了这个进程。

确切地说，人与蚂蚁之间的区别在于，我们会尝试用语言表达、存储、传输、理解和改进算法。然而，我们有时也会用到不知该如何用语言表达的算法。比如，我们很容易就能辨认出猫和狗，却难以解释是如何做到的：是计算腿和耳朵的数量呢？还是观察头的形状或毛发的纹理呢？

我们的大脑和身体会用很多算法来思考、运动、做事，但不管是符号算法，还是其他算法，我们并不总知道如何解释。

指令序列之外

从巴纽火车站到高等师范学院的算法可以表示成一个包含四个基本动作的逻辑序列：“取道东南方，向上朝着兰斯街的杜邦皇家大道”“然后……”“接着……”“再然后……”。欧几里得算法表达式中也出现了一些基本指令，比如赋值：“用b 替代a”。此外还有将这些指令封装成逻辑序列的句法结构，比如“这样做，然后那样做”，以及循环体，比如“当某条件为真时，重复此操作”。我们还可以添加条件测试语句：“如果此条件为真，那么这样做。”

这种方式听起来有点不寻常。事实上，只要很少的句法结构，就足以表达所有的符号算法，例如上述四个句法结构：赋值、逻辑序列、循环体、条件测试语句。算法的宝贵之处并不在于其组成有多么复杂，而恰恰在于这种将几个简单成分封装在一起的方式。

这就好比化学分子：数十亿个化学分子组成了我们所熟知的几十种化学元素；而这些化学元素本身仅由三种基本粒子——质子、中子和电子组成。

然而，尽管构建算法的基本元素在理论上非常充足，人们却很少从头开始构建算法：算法往往由其他一些已知的算法构成。例如，我们用算法描述了从巴纽地铁快线站到高等师范学院的路线。如果我们现在想从卢森堡公园到达校园的话，那么一个简单的算法就是：先乘坐地铁快线从卢森堡站到巴纽站，然后再运用先前的算法——这个算法被看成是一个整体。此时，一个全新的算法就这样形成了。我们并不清楚先前算法的细节，而是把它视为一个新的基本指令。

算法和数据

能够解决符号信息问题的算法，更注重这些符号信息的呈现方式。例如，为了更好地执行加减乘除运算的算法，用阿拉伯数字形式的算式123 × 456，比写成罗马数字的算式CXXIII × CDLVI 更好。同样，在字典中查找单词，用字母表查找比用象形文字查找更简单。

寻找从一个点到另一个点路径的算法，同样在意数据的表达形式。如果某个城市的地图像照片一样，一个像素接一个像素地被给出，那就很难找到想要的路径。最好可以用综合的方法去描述，比如整合各个十字路口，通过连接街道，赋予每一段路一个长度。这样一来，与其费力地从一个像素移动到另一个像素，不如从一个十字路口跳到另一个十字路口的算法来得轻巧。

算法的方法

已知的算法有很多，例如“分治法”“枚举测试法”“贪心算法”“随机算法”等。

“分治法”是把一个复杂的问题拆分成两个较为简单的子问题，进而两个子问题又可以分别拆分成另外两个更简单的子问题，以此类推。问题不断被层层拆解。然后，子问题的解被逐层整合，构成了原问题的解。高德纳曾用过一个邮局分发信件的例子对“分治法”进行了解释：信件根据不同城市区域被分进不同的袋子里；每个邮递员负责投递一个区域的信件，对应每栋楼，将自己负责的信件分装进更小的袋子；每个大楼管理员再将小袋子里的信件分发给对应的公寓。

最伟大的计算机程序员之一

高德纳（又译唐纳德•克努斯）生于1938 年，是著名的计算机科学家，也是现代算法的先驱之一。他的系列巨著《计算机程序设计艺术》在计算机科学界享誉多年。多年前，高德纳对现有的数学文本处理工具感到不满，于是创建了自己的工具 TeX 和 Metafont。如今，这两个工具成为广泛应用的免费软件。很多著名的算法都以他的姓氏命名，如克努斯- 莫里斯- 普拉特算法、罗宾逊- 申恩- 克努斯算法、克努斯-本迪克斯算法。

“枚举测试法”列举出待解决问题的所有可能解，然后逐一进行检验，最后从中找出符合要求的解。举个例子，一位旅行推销员必须依次访问几个不同城市拜访客户，他通常会寻找几个城市之间的最短回路，来安排自己的旅程。寻找最短回路的算法旨在计算所有可能的回路。例如有10 个客户，依次拜访10 个客户共有 10! = 3 628 800 种回路组合方式，分别计算每种组合方式的回路长度，然后选择最短的那条。

当枚举测试法所需的计算量太大时，使用“贪心算法”能够找到一个合理的解决方案，使问题结果最优化。比如，当旅行推销员有 20 位客户要访问时，用枚举测试法可能需要测试超过 2 兆条可能的路线。与其这样一个个枚举，不如就地运行另一个算法：推销员每次都从当前所在城市选择去往距离自己最近的下一个城市，以此类推。这个算法会选择当前最短距离作为计算的公里数，而且，永不退回到曾经选择过的路线上。一般来说，贪心算法找到的解决方案可能不是最好的，但却是“合理的”。

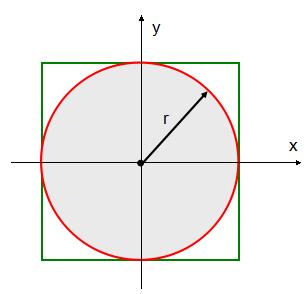
我们之前见过一个使用“随机算法”的例子：为了找到食物，侦察蚁从随机浏览蚁穴四周开始。同样，许多其他算法也用到了随机源。比如，“蒙特卡洛算法”能确定正方形内一个复杂图形的面积：在正方形中随机抽取一个点，就像扔飞镖一样，飞镖落在哪个点就取哪个点；大数定律告诉我们，这些点落入复杂图形内的频率接近于复杂图形面积和正方形面积之比。

利用蒙特卡罗算法求 π 的近似值

机器学习

我们要讨论到的最后一个方法是“学习程序”。学习做面包、在字典中查找单词，人类对此习以为常。但很多人可能想不到，算法也可以学习。就像面包师每天能从自己的工作中学习、提高一样，算法也可以从重复相同的任务中学习、进步。

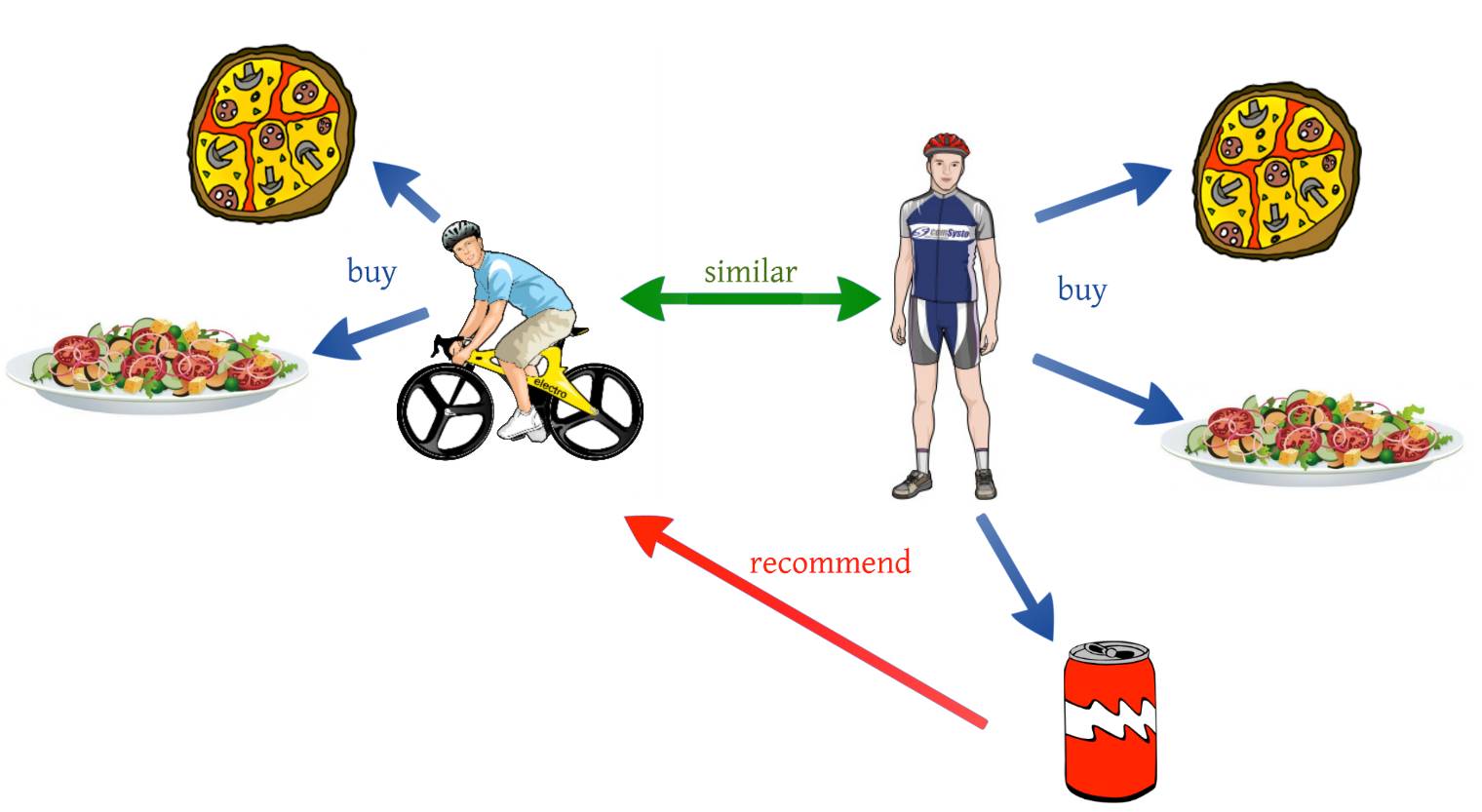
音乐、视频、图书分享平台上使用的“推荐算法”就是一种会学习的算法。系统程序会向用户推荐：“如果你喜欢《亚瑟王》，那你应当也喜欢《彼得•格里姆斯》。”提出这样的推荐，系统并不是基于亨利•珀塞尔和本杰明•布里顿之间的联系①。简单地说，系统的判断是基于对之前用户的听歌记录的分析：事实上，那些听过《亚瑟王》的用户之中，确实有很多人也听了《彼得•格里姆斯》；或者，算法尝试寻找一些我们可能并不认识，但品味却与我们接近的用户。在这两种情况下，算法学习、发现、统计了歌曲之间或者用户之间的相似性。从这样的学习程序出发，算法可以预测用户可能喜欢什么样的音乐，并因此会忍不住收听或者购买其他哪些作品。

①　亨利•珀塞尔和本杰明•布里顿分别为歌剧《亚瑟王》和《彼得•格里姆斯》的作曲家，布里顿的作曲风格深受珀塞尔的影响。——译者注

这些会学习的算法有助于我们重新审视自身的学习方式。推荐算法既没有认识到珀塞尔和布里顿之间的联系，也不需要拥有任何专业的音乐史知识。它只是对用户的选择进行观察，并从所见所闻中学习。事实上，这与一个孩子学习母语的过程没什么两样——从观察周围说话的人开始，然后用大量时间去模仿，不需要理解语法、动词变位和动宾搭配的问题。一个小孩知道应该说“我去学校”，而不是说“我走学校”，却无法解释为什么。正如推荐算法会向用户推荐本杰明•布里顿，却不能解释为什么用户可能喜欢这个作曲家。

推荐系统简单示例

有些学习程序的问题很难解决。假如我们要识别物体，如一只狗、一只猫、一张桌子，等等。在一张图像中，数据以像素的形式呈现，通过统计分析图像中的黑色或者蓝色像素点，很难区分这是一只狗还是一张桌子。这时，必须使用更复杂的学习算法——深度学习算法。深度学习算法首先尝试从图像中找到直线、圆、爪子、腿、桌脚……然后再寻找越来越复杂的物体对象。算法同样也是逐步建立越来越抽象的图像表达，最终找到被识别的物体。难点是，算法如何知道需要识别哪一种元素？是爪子、腿，还是桌脚？没关系，算法会通过自身的经验进行学习。例如，深度学习算法可以让下围棋的程序取得巨大进步，打败最优秀的人类围棋选手。