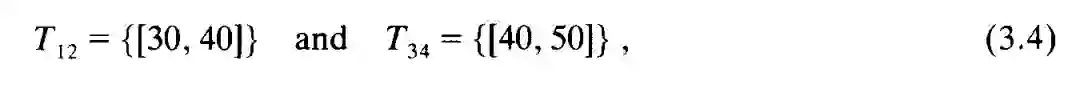30年前的热门研究，今获经典论文奖，贝叶斯网络之父旧论文「考古」

机器之心报道

编辑：魔王、蛋酱、张倩

一篇 30 年前的论文，因为一次获奖，又重新出现在世人眼前。

近日，图灵奖得主、贝叶斯网络之父 Judea Pearl 在推特上提到，自己在三十年前与当时的博士生 Rina Dechter、Itay Meiri 合著的论文《时间约束网络（Temporal Constraint Networks）》，获得了由人工智能顶级国际期刊 AIJ 颁发的 2020 年经典论文奖。

这篇论文发表于 1991 年，涉及的主题是上世纪八十年代的热门话题——时间约束。目前，该论文在谷歌学术上的被引用次数接近 2500。论文一作 Rina Dechter 被认为是「深度学习」一词的首倡者。

这篇论文的获奖理由如下：

这篇影响深远的论文介绍了用于定量时间推理的时间约束满足问题（TCSP）。TCSP 及其特例——简单时间问题（STP，可在多项式时间内解决）在规划、调度等应用中得到广泛使用。该论文中简洁优雅的问题描述为后续多个方向的研究提供了启发，包括时间不确定性、偏好和其他扩展问题。

论文内容简介

论文链接：http://ftp.cs.ucla.edu/pub/stat_ser/r113-L-reprint.pdf

这篇论文将基于网络的约束满足方法进行扩展，使其包含连续变量，从而为处理时间约束提供了框架 。在这个叫做时间约束满足问题（TCSP）的框架中，代表时间点和时间信息的变量由一组一元和二元约束进行表示，每一个指定一组时间间隔。该框架的独特特征在于允许处理度量信息，即评估不同事件之间的时间差。

该论文展示了一些算法，它们可用于执行以下推理任务：找到给定事件发生的所有合理时间；找到两个给定事件之间的所有可能关系；生成与给定信息一致的一个或多个场景。

该论文对简单时间问题（STP）和通用时间问题进行区分，前者对任意一对时间点至多认可一个间隔约束（interval constraint）。该研究表明，包含 Vilain 和 Kautz 点代数主要部分的 STP 可以在多项式时间内解决。对于通用 TCSP，该研究展示了一种执行三个推理任务的分解机制，并提出了多种能够改善效率的技术。此外，这篇论文还研究了路径相容算法在预处理时间问题上的适用性，展示了其终止，限制了其复杂度。

研究贡献

这篇论文提出了一种基于约束网络形式的时间推理统一方法。使用约束网络形式，该研究做出了以下几点贡献：

1. 为相关的多种算法机制提供了形式化基础，从而允许分析其复杂度和应用范围；

2. 提供了一种成本较低的表示——minimal network，它可以编码成对事件点之间的所有时间关系，包括时间差的绝对界限；

3. 提出了一种基于给定约束，高效生成特定时间场景的机制。

示例详解

作者在论文中给出了一个例子，示例中出现了多个事件和时间点，并利用这个示例介绍了该研究的主要思想。具体示例如下所示：

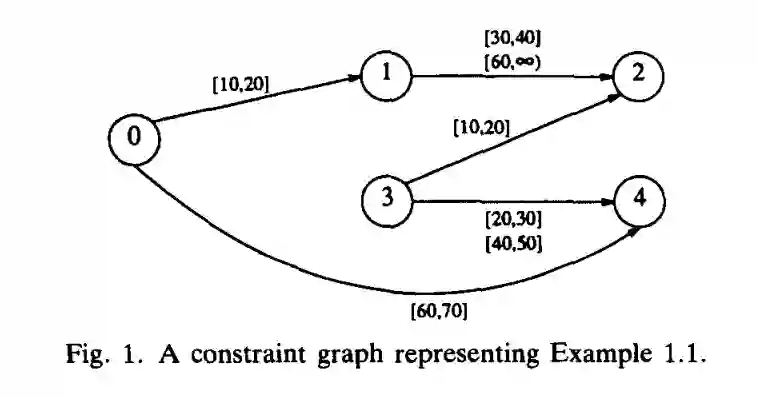
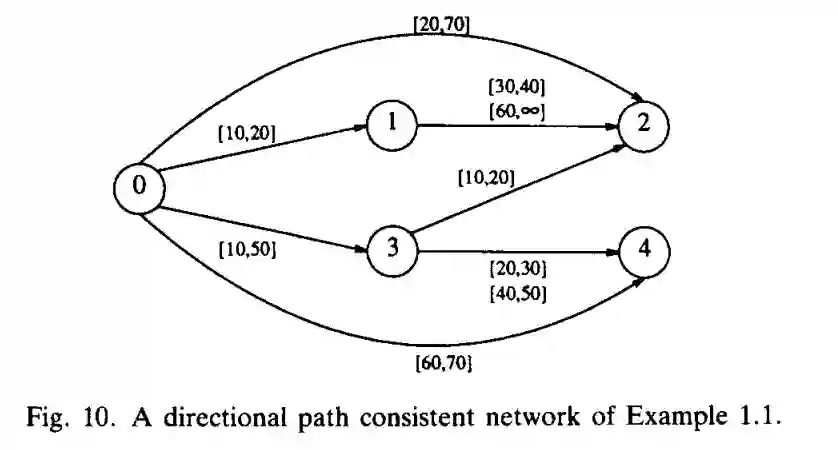
二元约束网络（二元 TCSP）包括一组变量 X_1 ..... X_n，和一组一元和二元约束。这样的网络可被表示为一个有向约束图。同理，示例 1.1 也可表示为有向约束图，如下图 1 所示：

该研究对基于约束的二元运算进行了定义：并集（union）、交集（intersection）和组合（composition）。

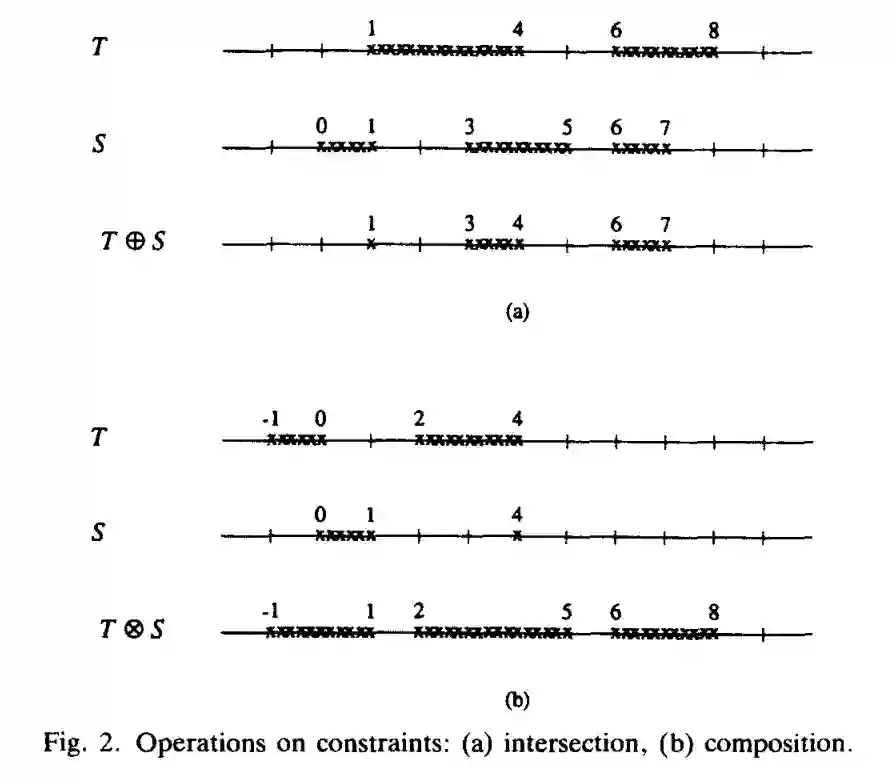
下图 2 展示了交集和组合运算：

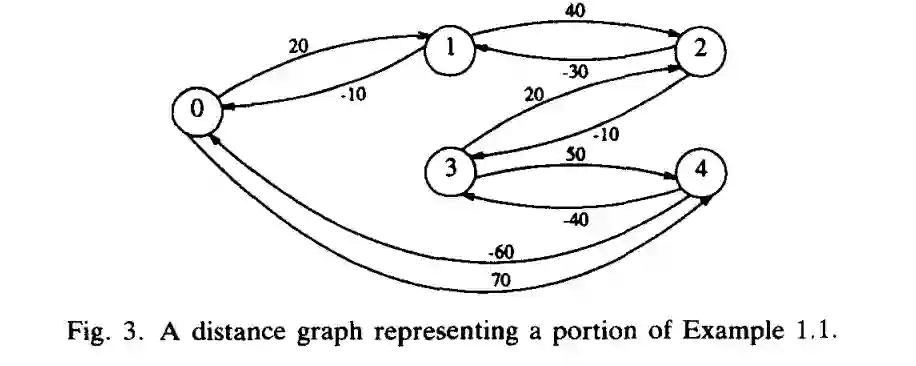
当 TCSP 中所有约束指定一个间隔时，这是一个简单时间问题（STP）。该研究将 STP 和有向边缘权重图（directed edge-weighted graph）联系起来，这类图叫做距离图（distance graph）。

假设示例 1.1 中 John 用汽车，Fred 用拼车，则我们可以得到一个 STP：

其距离图如下图 3 所示：

基于图 3，我们可以得到对应的 minimal network，如下所示：

现在回到通用 TCSP 问题，关于这类问题，有如下定理：

一种解决通用 TCSP 的直接方式是：将其分解为多个 STP，然后各个击破，最后再把结果组合起来。

示例 1.1 的 minimal network 参见下表 3：

此外，该论文介绍了路径相容算法及其弱化版本——有向路径相容在 TCSP 框架中的适用性。

给出一个 TCSP T，及其相关的约束图  G = (V, E) 和排序 d，通过 DPC 算法可以实现有向路径相容。

在示例 1.1 中，当排序 d = (0, 1, 2, 3, 4) 时应用 DPC 算法，可以得到如下网络：

Rina Dechte 与 Judea Pearl

AIJ 经典论文奖旨在表彰 15 年前（或更早）对 AI 领域产生重大影响的杰出论文，此次获奖的论文甚至发表于 30 年前。当时，人工智能领域还没有迎来第三次发展高潮，几位获奖者也是当之无愧的领域先驱人物。

「Deep Learning」概念提出者 Rina Dechter

这篇论文的一作 Rina Dechter 曾是 Judea Pearl 指导的博士生，她 1973 年在希伯来大学取得数学与统计学士学位，1985 年在加州大学洛杉矶分校取得计算机科学博士学位。研究领域为人工智能中的自动推理。

在论文《Temporal Constraint Networks》发表的同年，Rina Dechter 获得了美国国家科学基金会颁发的总统青年研究者奖。

1996 年，Rina Dechter 成为加州大学欧文分校（UC Irvine）的正式教授，并工作至今。Rina Dechter 于 1994 年当选为 AAAI Fellow，后又于 2013 年当选为 ACM Fellow。2011 年到 2018 年间，她担任 AIJ 杂志的联合主编。

值得一提的是，Rina Dechter 被认为是提出术语「深度学习」的人。尽管多层感知器是在 1965 年发明的，1971 年也出现了一个 8 层神经网络，但「深度学习」一词是 Rina Dechter 于 1986 年率先在论文中使用的。

Rina Dechter 在 1986 年的论文《LEARNING WHILE SEARCHING IN CONSTRAINT-SATISFACTION-PROBLEMS》中首次提到「deep learning」。

贝叶斯网络之父、图灵奖得主 Judea Pearl

比 Rina Dechter 更有声望的，是她的导师 Judea Pearl。

提到 Judea Pearl，机器学习领域的读者应该不会陌生。他是美国计算机科学家和哲学家，以倡导人工智能的概率方法和贝叶斯网络的发展而闻名，建立了基于结构模型的因果和反事实推理理论。2011 年，Judea Pearl 获得计算机科学最高奖项图灵奖，获奖理由是：「通过发展概率和因果推理的微积分对人工智能做出了重大贡献」。

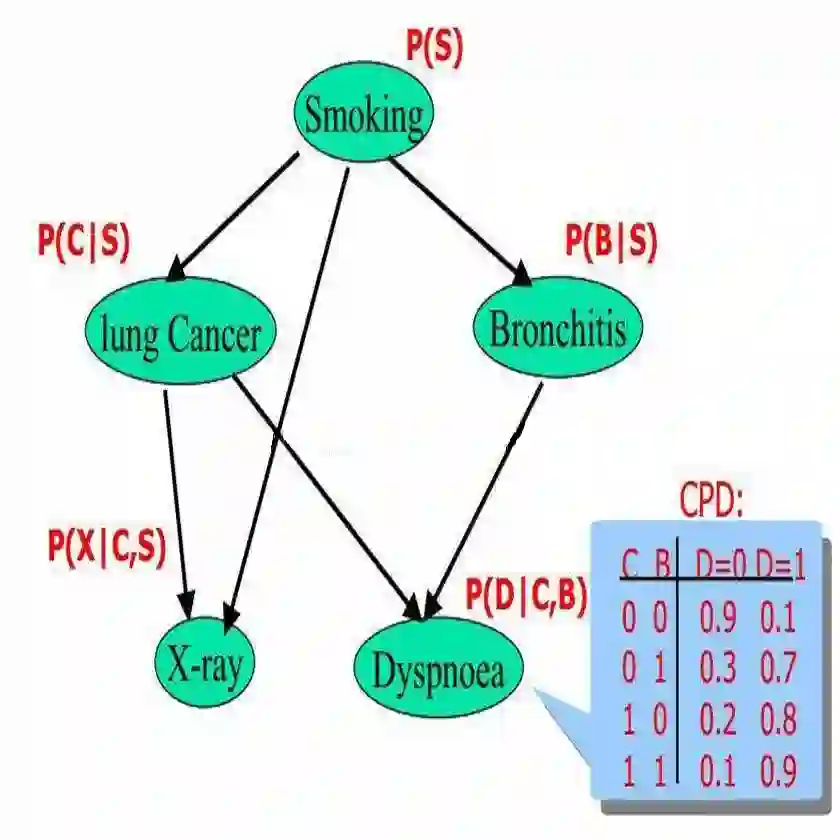
30 年前，人工智能研究的一个主要挑战是对机器进行编程，以便将潜在的原因与一系列可观察到的情况联系起来。Pearl 用一种叫做「贝叶斯网络」的方案来解决这个问题。贝叶斯网络可以让机器回答这样一个问题——给出一个从非洲回来的发烧且身体疼痛的病人，他 / 她最有可能患上的是疟疾。2011 年，Pearl 获得图灵奖，这很大程度上要归功于贝叶斯网络。

但在 Pearl 看来，人工智能领域已经陷入了概率关联（probabilistic association）的泥潭。近几年，新闻头条吹捧机器学习和神经网络的最新突破，比如计算机可以下围棋和驾驶汽车。但 Pearl 对此感到腻味。在他看来，当今人工智能领域的最新技术仅仅是上一代机器所做事情的强化版：在大量数据中找到隐藏的规律。他曾表示：「 所有令人印象深刻的深度学习成果都只是曲线拟合 。」

那么，怎样才能推动 AI 社区解决这一问题呢？在之前的采访中，Pearl 认为，我们需要一场「因果革命」。研究者应该考虑采用因果推断模型，从因果而非单纯的数据角度进行研究。他认为，我们在过去一段时间错过了对因果推断的研究机会，这原本是科学研究的核心：寻找变量的因果关系。

在很长一段时间里，统计机器学习主要关注对表征的拟合，寻找的是变量之间的相关性，而非潜在的因果性。这样的认识使科学研究停留在较浅的关联层面，导致模型的鲁棒性和可解释性丧失，阻断了进一步探究干预变量以及反事实推断（即假设某一变量完全相反而其他变量不变时，该变量对结果的影响）的能力。Pearl 认为，智能的机器应该能够彼此沟通交流，通过提出反事实对话（如「你应该怎样做」）而作出更好的表现。

基于此，Pearl 和他的同事在 2018 年完成了著作《The Book of Why: The New Science of Cause and Effect》。Pearl 在书中详细地阐述自己在这一领域的研究成果，希望能够促进人们反思当前的研究方向。

Pearl 期望因果推理能为机器提供人类水平的智能。他解释说，它们可以更有效地与人类沟通，甚至可以获得道德实体（moral entity）的地位，具有自由意志和作恶的能力。

Judea Pearl 及其学生的思想经过了时间的洗礼，在 30 年后重新获得认可。对此，Pearl 调侃说，「感觉自己像只恐龙」。也许，这正是投身于科学研究的魅力所在。

参考链接：

https://en.wikipedia.org/wiki/Rina_Dechter

https://www.ics.uci.edu/~dechter/new_site/cv.pdf

https://www.sohu.com/a/209613608_99964548

机器之心 ECCV 2020 线上分享第一期，我们邀请到暗物智能研究副总监苏江博士为我们分享 Oral 论文《EagleEye: Fast Sub-net Evaluation for Efficient Neural Network Pruning》。

在此论文中，研究者们提出了一种性能极高的剪枝算法 EagleEye。欢迎读者报名参与。

© THE END 

转载请联系本公众号获得授权

投稿或寻求报道：content@jiqizhixin.com