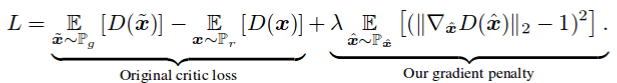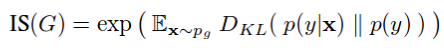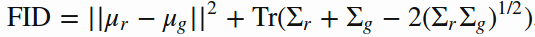生成对抗网络的最新研究进展

2019 年 2 月 6 日 AI科技评论

AI 科技评论按，生成对抗网络是一类功能强大、应用广泛的神经网络。它们基本上是由两个神经网络组成的系统——生成器和判别器，这两个网络相互制约。计算机视觉和人工智能的爱好者 Bharath Raj 近日发布以一篇博文，总结了生成对抗网络的原理、缺点和为了克服这些缺点所做的研究的最新进展。雷锋网 AI 科技评论编译整理如下：

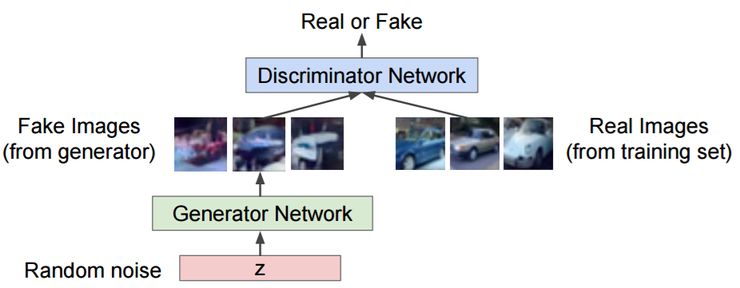
生成对抗网络的工作原理

给定一组目标样本，生成器试图生成一些能够欺骗判别器、使判别器相信它们是真实的样本。判别器试图从假（生成）样本中解析真实（目标）样本。使用这种迭代训练方法，我们最终得到一个真正擅长生成类似于目标样本的样本的生成器。

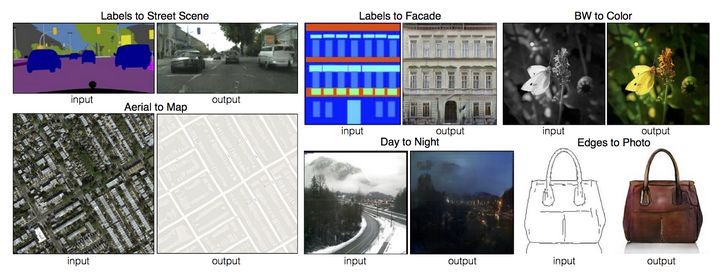
GAN 有大量的应用程序，因为它们可以学习模拟几乎任何类型的数据分布。一般来说，GAN 可以用于处理超低分辨率的图像以及任何类型的图像翻译等等，如下所示：

使用 GAN 进行图像翻译

然而，由于其变化无常、表现不稳定，很难用它们做一些事情。当然，许多研究人员已经提出了很好的解决方案，以减轻 GAN 网络训练中所涉及到的一些问题。然而，这一领域的研究进展速度如此之快，以至于人们来不及去追踪很多有趣的想法。这个博客列出了一些常用的使 GAN 训练表现稳定的技术。

使用 GAN 的缺点概述

GAN 很难用的原因有很多，本节的下面将列出其中一些原因。

1.模型崩溃（Mode collapse）

自然数据分布是高度复杂和多模态的。也就是说，数据分布有很多「峰值」或「模型」。每种模型代表相似数据样本的浓度，且不同于其他模型。

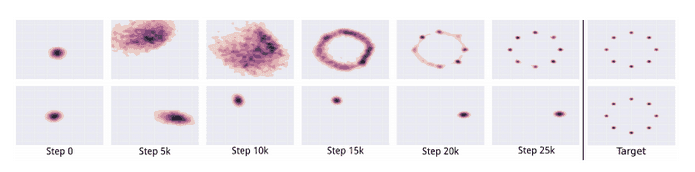
在模型折叠期间，生成器生成属于一组有限模型的样本。当生成器相信它可以通过锁定到单个模型来骗过判别器时，就会发生这种情况。也就是说，生成器仅从该模型生成样本。

顶部的图像表示没有模型折叠的 GAN 的输出，底部的图像表示模型折叠时的 GAN 输出。

判别器最终发现这个模型的样本是假的。因此，生成器只需锁定到另一个模型。这个循环无限重复，这基本上限制了生成样本的多样性。要获得更详细的解释，您可以查看此日志。

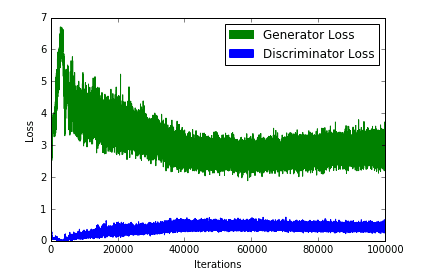
2.收敛

在 GAN 训练中，一个常见的问题是「我们什么时候停止训练它们？」「。由于判别器损耗降低（反之亦然）时，生成器损耗会增加，因此不能根据损耗函数的值判断收敛性。如下图所示：

典型 GAN 损失函数图，请注意为何这张图不能解释收敛性。

3.质量

与前面的问题一样，很难定量地判断生成器何时会生成高质量的样本。在损失函数中加入额外的感知正则化可以在一定程度上缓解这种情况。

4.度量

GAN 的目标函数解释了和其对手相比，它的生成器或者判别器表现如何。然而，它并不代表输出的质量或多样性。因此，我们需要不同的度量标准来度量相同的内容。

术语

在深入研究有助于提高性能的技术之前，让我们回顾一下一些术语。这将有助于理解下一节中所介绍的技术。

1.上确界和下确界

简而言之，下确界是集合的最大下界，上确界是集合的最小上界。它们不同于最小值和最大值，因为上确界和下确界不一定属于集合。

2.散度度量

散度度量表示两个分布之间的距离。传统的 GAN 神经网络基本上最大限度地减少了真实数据分布和生成数据分布之间的 Jensen Shannon 分歧。GAN 损失函数可以修改，以尽量减少其他散度度量，如 Kulback-Leibler 散度或总变化距离。

3.Kantorovich Rubenstein 对偶性

一些散度度量措施难以以其初始形式进行优化。然而，他们的对偶形式（用下确界代替上确界或者用上确界代替下确界）可能易于优化。对偶原则为将一种形式转换为另一种形式奠定了框架。关于这一点的详细解释，你可以查看这篇博客。

4.Lipschitz 连续性

一个 Lipschitz 连续函数的变化速度是有限的。对 Lipschitz 连续函数来说，函数曲线上任一点的斜率的绝对值不能超过实值 K。这样的函数也被称为 K-Lipschitz 连续函数。

Lipschitz 连续性对 GAN 网络来说是必须的，因为它们会限制判别器的斜率。另外，Kantorovich-Rubinstein 对偶性要求它是 Wasserstein GAN。

提高性能的技术

有许多技巧和技术可以用来使 GAN 更加稳定和强大。在这篇博客中，为了简洁起见，我只解释了一些相对较新或复杂的技术。在本节末尾，我列出了其他各种方法和技巧。

1.损失函数

关于 GAN 的缺点，最受欢迎的修复方法之一是 Wasserstein GAN。它的基本原理是用地球移动距离（Wasserstein-1 distance 距离或 EM 距离）取代了传统的 GAN 的 Jensen Shannon 发散。EM 距离的原始形式是难以处理的，因此我们使用它的对偶形式（由 Kantorovich-Rubenstein 对偶计算）。这就要求判别器是 1-lipschitz，它通过剪切判别器的权重来保持。

使用移动距离的优点是，它是连续的，即使实际和生成的数据在分布上没有交集。此外，生成的图像质量与损失值（源）之间存在相关性。缺点是，对每个生成器更新，我们都需要根据原始实现来进行判别器更新。此外，作者声称，降低权重是确保 1-lipschitz 约束的一种糟糕方法。

与 Jensen-Shannon 散度（右）不同，地球运动距离（左）是连续的，虽然它的分布不是连续的。有关详细说明，请参阅这篇文章。

另一个有趣的解决方案是使用均方损失而不是对数损失。LSGAN 的作者认为，传统的 GAN 损失函数并没有提供太多的激励来「拉动」生成的数据分布接近真实的数据分布。

原始 GAN 损失函数中的对数损失不影响生成数据与决策边界之间的距离（决策边界将真实和虚假数据分开）。另一方面，LSGAN 对远离决策边界的生成样本进行惩罚，本质上是将生成的数据分布「拉近」实际数据分布。它通过用均方损失代替对数损失来做到这一点。有关这一点的详细解释，请访问此博客。

2.两个时间刻度更新规则（TTUR）

在这种方法中，我们对判别器和生成器使用不同的速率进行学习。通常，生成器使用较慢的更新规则，判别器使用较快的更新规则。使用这种方法，我们可以以 1:1 的比率执行生成器和判别器更新，且只需调整学习速率。值得注意的是，SAGAN 实现使用了此方法。

3.梯度惩罚

本文改进了 WGAN 的训练，作者声称，降低权重（最初在 WGAN 中执行）会导致优化问题。他们声称，权重的降低迫使神经网络学习「更简单的近似」达到最佳的数据分布，导致低质量的结果。他们还声称，如果 WGAN 超参数设置不正确，那么降低权重会导致梯度问题爆发或者消失。作者在损失函数中加入了一个简单的梯度惩罚，从而减轻了上述问题。此外，1-lipschitz 的连续性保持不变，正如最初的 WGAN 实施一样。

DRAGAN 的作者认为，当 GAN 玩的游戏（即判别器和生成器相互对抗）达到「局部平衡状态」时，模式就会崩溃。他们还认为，这些判别器所产生的梯度是「尖锐的」。当然，使用梯度惩罚将有助于我们绕过这些状态，大大提高稳定性，减少模式崩溃。

4.谱归一化

谱归一化是一种权重归一化技术，通常用于判别器以强化训练过程。这基本上确保了判别器是 K-Lipschitz 连续的。

像 SAGAN 这样的一些实现也在生成器上使用了谱归一化。文中还指出，该方法比梯度惩罚法计算效率高。

5.展开和打包

正如这篇优秀的博客所述，防止模式崩溃的一个方法是在更新参数时预测对策。当判别器有机会作出反应（考虑到反作用）后，展开的 GAN 使生成器能够愚弄判别器。

另一种防止模式崩溃的方法是「打包」属于同一类的几个样本，然后将其传递给判别器。这种方法被纳入了 PacGAN 中，在这里有模式崩溃的减少的报道。

6.成堆的 GAN

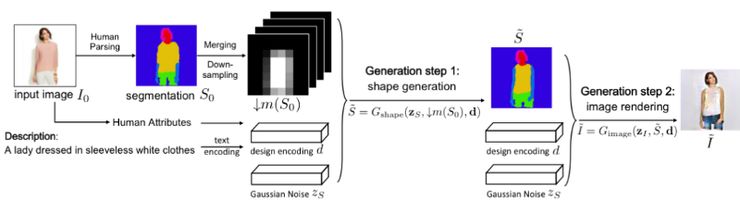
单个 GAN 可能不够强大，无法有效地处理任务。我们可以使用连续放置的多个 GAN，其中每个 gan 解决问题的一个更简单的版本。例如，FashionGAN 使用两个 GAN 来执行本地化图像翻译。

Fashiongan 使用两个 gan 来执行本地化图像翻译

把这个概念推向极端，我们可以逐渐增加向我们的 GAN 提出的问题的难度。例如，渐进式 GAN（ProGAN）可以生成高质量、高分辨率的图像。

7.Relativistic GANs

传统的 GAS 测量生成数据真实的概率。Relativistic GANs 测量生成的数据比实际数据「更真实」的概率。我们可以使用一个合适的距离来测量这个「相对真实性」，正如「RGAN」论文中所提到的那样。

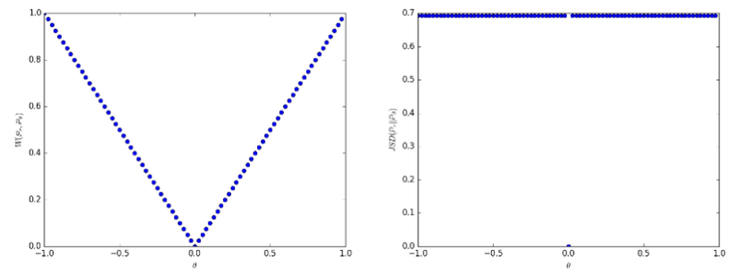
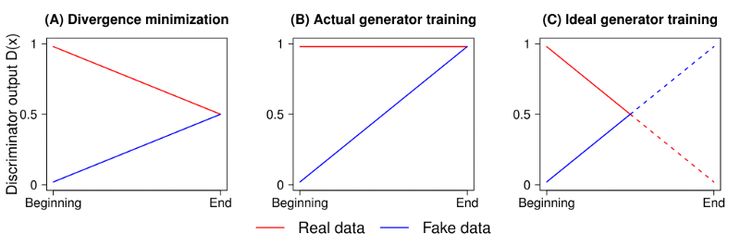
当使用标准 GAN（图 B）损失的时候，生成器的输出。图 C 是输出曲线的实际样子。图 A 表示 JS 散度的最优解。

作者还提到，当判别器输出达到最佳状态时，它应该收敛到 0.5。然而，传统的 GAN 训练算法强制判别器为任何图像输出「真实」（即 1）。这在某种程度上阻止了判别器达到其最佳值。Relativistic GANs 也解决了这个问题，并且有相当显著的结果，如下所示。

经过 5000 次迭代后的标准 GAN（左）和 Relativistic GAN（右）的输出。

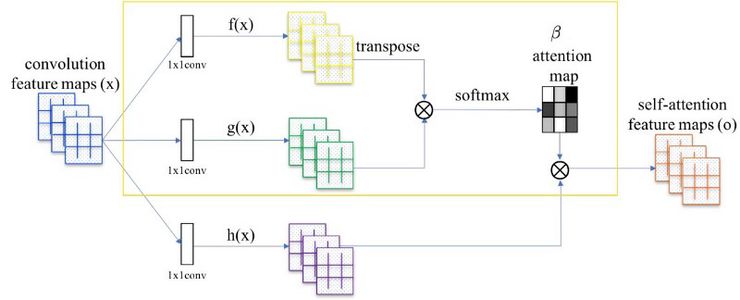
8.自我关注机制

「Self Attention GANs」的作者声认为，用于生成图像的卷积着眼于局部传播的信息。也就是说，由于接受领域有限，这些卷积错过了全局关系。

将注意力图（在黄色框中计算）添加到标准卷积操作中。

自我关注生成对抗网络允许对图像生成任务进行关注驱动的远程依赖性建模。自我注意机制是对正常卷积运算的补充。全局信息（长距离相关性）有助于生成更高质量的图像。网络可以选择忽略注意机制，或者将其与普通卷积一起考虑。要获得详细的解释，你可以查看他们的论文。

以红点标记的位置的注意地图可视化。

其他技术

以下是一些附加技术的列表（并非详尽列表）用于改进 GAN 训练：

特征匹配
小批量鉴别
历史平均值
单面标签平滑
虚拟批处理规范化

你可以在这篇文章和这篇博文中了解更多关于这些技术的信息。在这个 GitHub 存储库中列出了更多的技术。

指标

既然我们已经知道了改进训练的方法，那么如何来证明呢？以下指标通常用来衡量 GAN 的性能：

1.初始得分

初始分数衡量生成数据的「真实性」。

初始分数

方程有两个分量 p（y_x）和 p（y）。这里，x 是由生成器生成的图像，p（y_x）是通过预先训练的初始网络（如在原始实现中对 ImageNet 数据集进行预训练）传递图像 x 时获得的概率分布。另外，p（y）是边缘概率分布，可以通过对生成图像（x）的几个不同样本求 p（y_x）的平均值来计算。这两个术语代表了真实图像所需的两种不同品质：

生成的图像必须具有「有意义」的对象（对象清晰，不模糊）。这意味着 p（y_x）应该具有「低熵」。换句话说，我们的初始网络必须可以非常清楚地确定生成的图像属于特定的类。
生成的图像应该是「多样的」。这意味着 p（y）应该具有「高熵」。换句话说，生成器应该生成图像，使每个图像代表不同的类标签（理想情况下）。

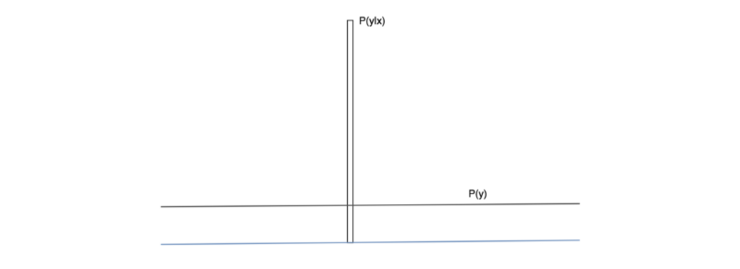
P（y_x）和 P（y）的理想图。像图中这样的一对会有很大的 kL 发散。

如果一个随机变量是高度可预测的，那么它的熵就很低（即 p（y）必须是一个具有尖峰的分布）。相反，如果它是不可预测的，那么它具有高熵（即 p（y_x）必须是均匀分布）。如果这两个特征都得到满足，我们就会认为 p（y_x）和 p（y）之间的 KL 差异很大。当然，一个大的初始分数（IS）是更好的。为了更深入地分析初始分数，您可以阅读这篇论文。

2.Fréchet 距离（FID）

初始分数的一个缺点是，实际数据的统计数据不会与生成数据的统计数据进行比较。Fréchet 距离通过比较真实图像和生成图像的平均值和协方差来解决这个缺点。Fréchet 初始距离（FID）执行相同的分析，但它通过预先训练的 inception-v3 网络传递真实和生成的图像而生成特征图。方程描述如下：