【HKUST博士论文】复杂任务下的元学习

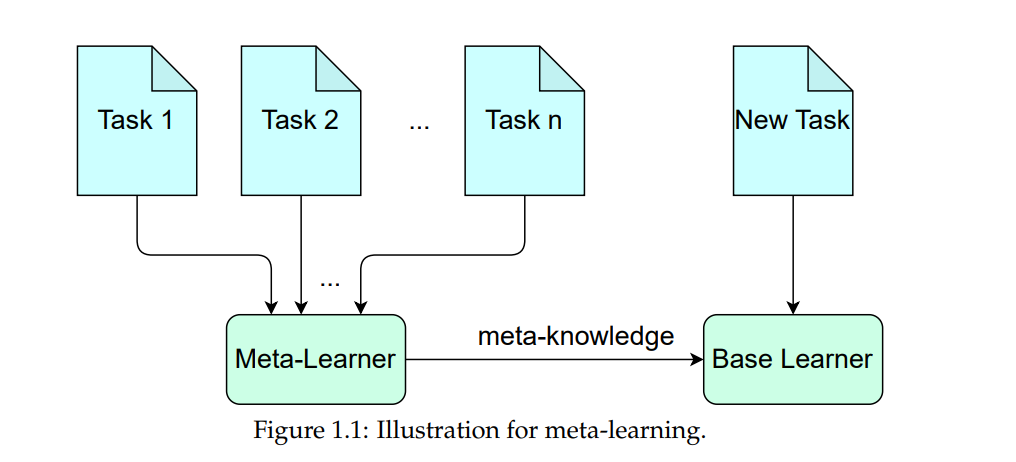
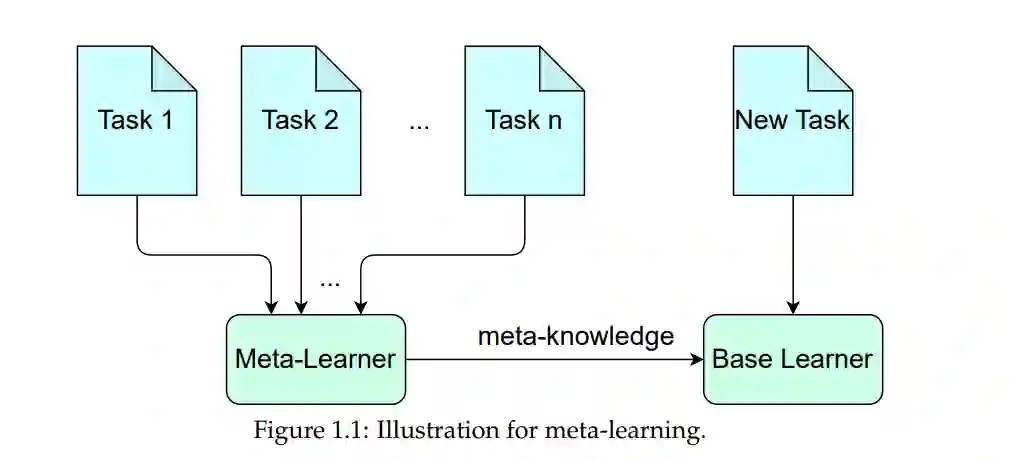
元学习旨在从历史任务中提取共享知识（元知识），以加速新任务的学习。在各种应用中，它已经取得了令人鼓舞的表现，并且开发了许多元学习算法来学习包含元知识的元模型（例如，元初始化/元正则化），以支持特定任务的学习过程。本文的重点是复杂任务下的元学习，因此，特定任务的知识是多样化的，且需要各种元知识。

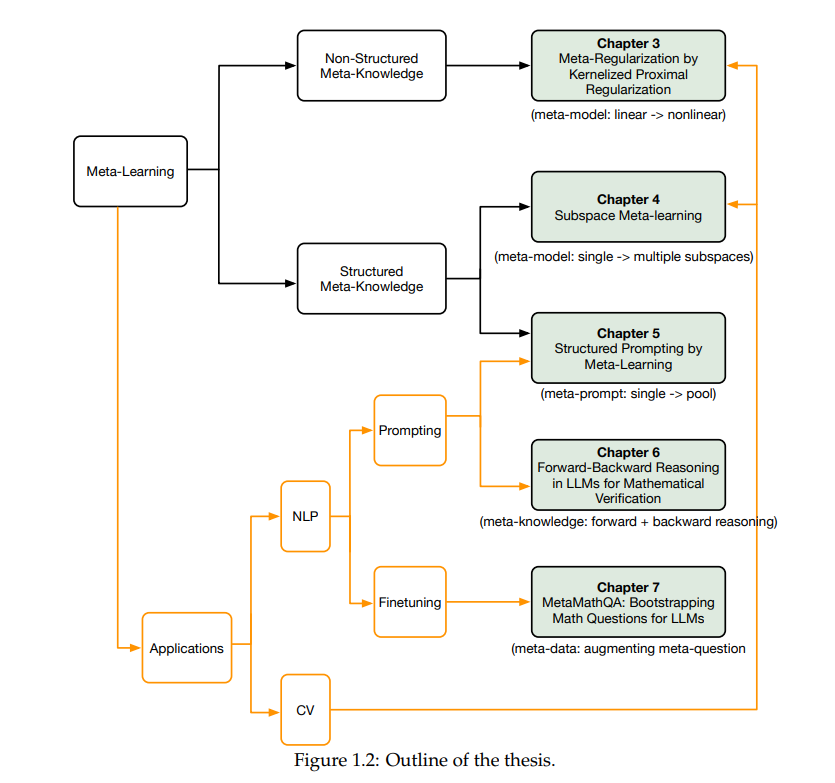
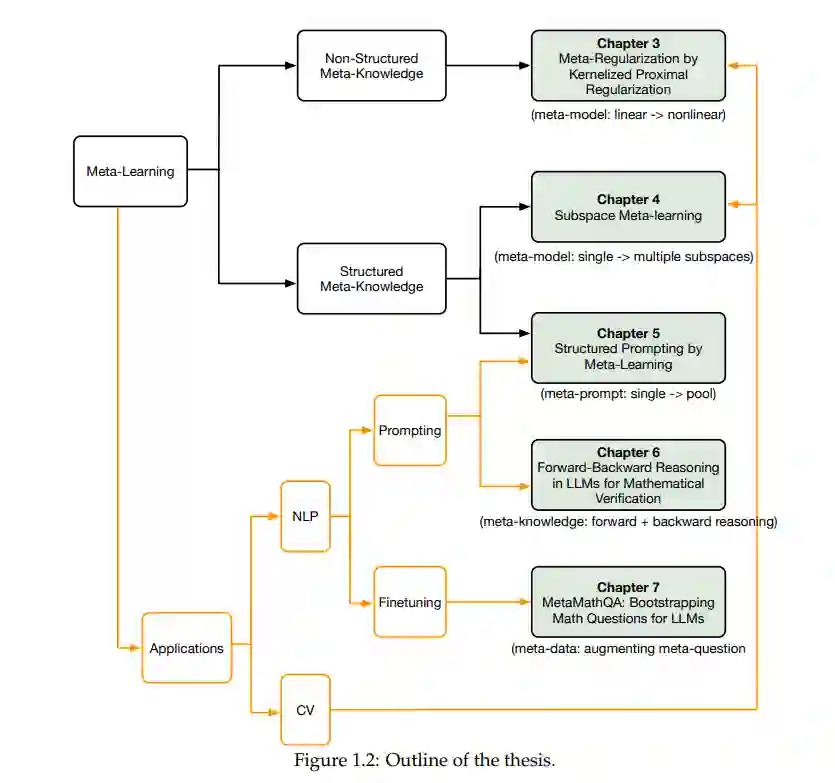
首先，我们通过核化近端正则化将线性模型的有效元正则化扩展到非线性模型，从而使得像深度网络这样更强大的模型能够处理复杂任务。 其次，我们将特定任务的模型参数形式化为一个子空间混合，并提出了一种模型无关的元学习算法来学习子空间基。每个子空间代表一种类型的元知识，结构化的元知识比简单的元模型更有效地加速复杂任务的学习。 第三，我们提出了一种高效且参数优化的元学习算法，用于自然语言处理任务中的提示调优。该算法学习一组多个元提示，从元训练任务中提取元知识，然后通过注意力机制将所有元提示的加权组合构建为实例依赖的提示。实例依赖的提示具有灵活性和强大功能，能够有效地处理复杂任务的提示。 接下来，我们使用大语言模型（LLM）研究数学推理任务。为了验证由LLM生成的候选答案，我们提出将前向和后向推理的元知识结合起来。 最后，我们提出了问题增强方法，通过扩展问题集来训练LLM，从而增强LLM的数学推理元知识。原始问题通过两个方向进行增强：在前向方向，我们通过少样本提示重新表述问题；在后向方向，我们对问题中的数字进行掩蔽，并创建一个反向问题，通过答案预测被掩蔽的数字。

‘

’