《异质再入飞行器的弹道导弹防御概率模型》2023最新46页报告

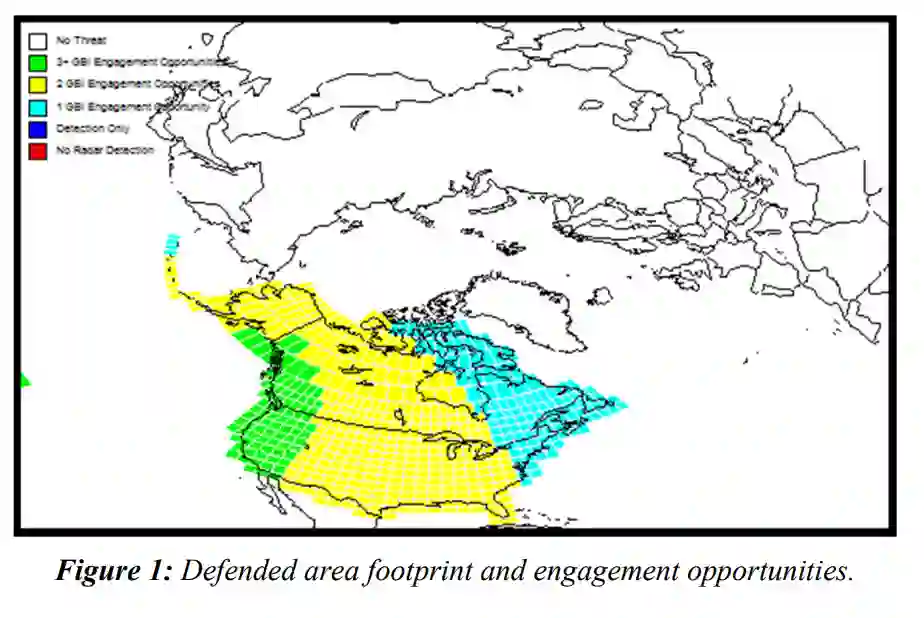
在这份科学报告中，研究了一个导弹防御的问题，其中有异质的来袭再入飞行器（RVs）。也就是说，这些再入飞行器由不同类型的导弹组成。防御系统利用也是导弹的拦截器来试图拦截再入飞行器。我们建议，在有异质RV的简单交战场景中，防卫方可以使用最佳最后交战机会（SLS-OLEO）的射击战术来优化其在最后交战机会中的突袭否定概率（PRA）。为了优化这种方法，我们利用天体动力学、带约束的微积分、微扰理论、动态规划和生成函数以及PRA的凹特性来比较各种射击战术。这种方法使我们能够确定针对RV的拦截器的最佳分配，使PRA最大化。此外，我们还考虑了PRA如何有助于综合系统有效性的概率（PISE），这反过来又决定了弹道导弹防御系统（BMDS）的全球有效性。原则上，该方法一般适用于导弹。然而，我们确定交战机会数量的方式是基于弹道导弹的。

对国防和安全的意义

在导弹防御方面，至关重要的是，防务部门要消除来袭的RV，以保护其资产和人口。众所周知，有一种基于RVs数量、拦截器数量及其特性（如单发杀伤概率（SSBK）和交战机会数量）的发射策略，可以最大限度地提高突袭否定的概率，即PRA。然而，当来袭的RV由不同类型的导弹组成时，这样的策略需要修改，因为现在的情况更复杂了。我们表明，用本报告所制定的策略仍有可能使PRA最大化。这一点很重要，因为最大化PRA意味着最大限度地挽救人口中的生命数量。

引言

对防空的作战分析可以追溯到1930年代（Kirby和Capey[1]）。从那时起，防空研究有了很大进展，特别是在导弹防御领域。目前关于弹道导弹防御系统（BMDS）的文献的特点是，分析集中在整个系统的孤立方面。具体来说，有关于理论发射理论（Soland [2]）、射-看-射战术（Wilkening [3]）、命中评估（Weiner等人，[4]）、轨道力学（Cranford [5]）和综合概率模型，如综合系统有效性概率（PISE）（Boeing Co [6]）的研究。相比之下，本科学报告侧重于突袭湮灭概率（PRA），它是PISE的一个核心组成部分，也是BMDS有效性的一个关键决定因素。

为了证明PRA的重要性，我们在涉及异质再入飞行器（RVs）的交战场景中比较了三种发射战术。在对结果进行严格的比较后，我们说明，虽然 "射击-观察-射击与最佳最后交战机会"（SLS-OLEO）没有产生最大的PRA，但它在一个简单的交战场景中提出了最实际有效的PRA。也就是说，我们并不假定来袭的RV的数量是完全已知的。我们还探讨了是什么使PISE成为BMDS框架的一个重要组成部分，并提出了两个可以提高PISE的战术。我们相信，作战研究界的成员将能够利用这些发现来评估BMDS的全球有效性。

为了帮助关注这个问题，我们定义了一个由五个异质再入飞行器（RVs）和二十个拦截器组成的例子情景，（Wilkening [3]）。这个场景当然不是一个饱和的场景，即RV的数量超过了拦截器的库存，正如（Dou等人，[7]）所调查的。由于弹道导弹防御（BMD）的复杂性，有些特点和方法我们无法在本报告中涉及或深入分析。与其他研究相比，我们的视角是单面的（仅是防御），而不是双面的（防御和进攻，Brown等人，[8]；两阶段博弈，Hausken和Zhuang[9]）。我们的研究也主要限于地基拦截器（GBI），而不是其他发射平台，如闲逛的飞机（Burk等人，[10]）。我们不考虑诱饵（Washburn[11]）。我们注意到，BMD也可以使用基于代理的模拟（Garrett等人，[12]和Holland等人，[13]），或使用马尔科夫链（Menq等人，[14]）进行建模。Park和Rothrock[15]研究了在导弹防御中框定人类主体的效果。实时威胁评估和武器分配（TEWA）的细节可以用3维稳定的婚姻算法来建模（Naseem等人，[16]）。针对一系列RV的防御性武器的最佳组合可以用线性编程来建模（Beare [17]）。尽管有这些假设和简化，我们相信我们的方法为理解BMD提供了一个简单的方法，同时也为评估BMDS的有效性提供了一个直接和统一的方法。

本文的组织结构如下：第2节描述了交战机会的数量；第3节介绍了三种已知的可用于对付相同（同质）RV的发射战术；第4节扩展了一些用于异质RV的发射战术，并提出了一种新的战术；第5节描述了PRA的凹性；第6节利用凹性来确定全球最佳PRA；第7节说明了有效性的措施；第8节讨论了PISE和改进它的方法；我们在第9节中得出结论。

本文是2014年发表的另一篇论文（Nguyen [18]）的完整和扩展技术版本，增加了一些新的内容，包括考虑新的射击战术（在第4节）、PRA的凹性（在第5节）和全局最优PRA（在第6节）。虽然第7节中的有效性措施在现有文献中可以获得，但我们根据第4、5和6节的新颖性来确定这些有效性措施。据我们所知，在文献中还没有任何论文将所有这些方面的内容汇集在一篇关于BMD的文章中。这篇文章的初步结果发表在一个会议记录中（Nguyen和Miah[19]），它利用遗传算法来优化有效性的措施。