【NeurIPS2023】宽度神经网络作为高斯过程:深度均衡模型的经验教训

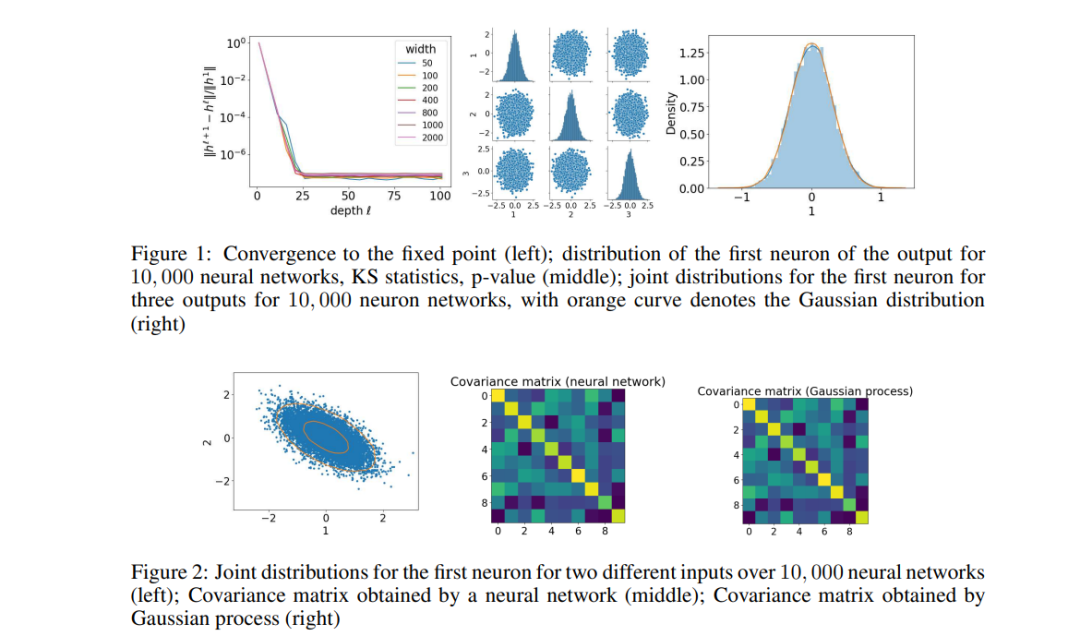
宽度神经网络因其与高斯过程的等价性而受到了极大的关注，这使得它可以完美地拟合训练数据，同时保持泛化性能，这被称为良性过拟合。然而，现有的研究主要集中在浅层或有限深度的网络上，这使得我们有必要对具有无限深度层的宽神经网络进行全面分析，例如神经常微分方程（ODEs）和深度平衡模型（DEQs）。在这篇文章中，我们特别研究了深度平衡模型（DEQ），一个在各层之间共享权重矩阵的无限深度神经网络。我们的分析揭示，随着DEQ层的宽度逼近无穷大，它会收敛到一个高斯过程，从而确立了所谓的神经网络与高斯过程（NNGP）对应关系。值得注意的是，即使深度和宽度的极限互换，这种收敛性仍然存在，这在典型的无限深度多层感知器（MLP）网络中并没有观察到。此外，我们证明了相关的高斯向量对于任何成对不同的输入数据仍然是非退化的，确保使用NNGP核的相应核矩阵具有严格正的最小特征值。这些发现为研究DEQs的训练和泛化提供了基本要素，为这一领域的未来研究奠定了基础。