《用于图像分类的分层模糊深度学习》美国陆军等2022最新论文

在过去的几十年里，人们对模糊逻辑及其应用表现出相当大的兴趣。智能和深度学习系统在各行各业都获得了突破性进展，以解决未来的实际问题。传统的模糊有限制，只能在有限的规则维度下工作，而深度神经网络则无法处理系统中隐含的不确定和不精确的数据。本文的目的是为智能系统开发一种能够处理不确定性和不精确行为的通用算法，特别是用于处理大型图像数据集。本文提出了分层模糊方法，因为它在解决现实生活中的大型问题方面越来越受到关注。所用的策略是将大的图像数据集划分为小的数据样本，并以分层的方式连接所有的模糊子系统。在文献中，据作者所知，没有人开发出一种分层模糊方法来处理真实图像的大型图像数据集。已经讨论了使用图像阈值处理大型图像数据的分层模糊逻辑的算法。为了进行评估，已经考虑了真实的图像数据库。图像分类已经在国防和安全领域取得了潜在的应用，特别是在目标识别和分类方面。分层模糊系统的准确性和计算时间与现有方法如深度神经网络的比较已经被讨论。

引言

Lotfi Zadeh在1965年提出了模糊逻辑[1], [2]的概念，处理信息的不确定性、不精确性或模糊性。模糊包括在数学和现实系统之间架起桥梁的语言参数。模糊逻辑起源于传统逻辑的合理化。它通过在假和真之间的稳定过渡来运行。传统逻辑将输出显示为 "0 "或 "1"，而模糊逻辑将结果显示为[0,1]范围内的真实程度。模糊逻辑应用了部分真实的理论，输出可能在完全真实和完全虚假之间摇摆。

模糊系统包括三个子系统：模糊器、推理系统和去模糊器。模糊化器将输入转换为语言值，这些语言值被视为模糊集的标签。推理系统拥有一个包含输入-输出关系选择的规则库。规则的数据集包括成员函数和输入与输出组合的规范化。去模糊器合并了推理系统的输出，并转化为非语言术语。

随着时间的推移，模糊系统的几个分支已经被开发出来[1], [3], [4], [5]，例如，神经模糊系统或模糊神经网络、模糊聚类、模糊逻辑图像处理等。随着神经网络的出现，模糊逻辑的概念已经扩展到神经模糊逻辑。模糊逻辑为包括人类评估的不确定性、不精确性和模糊性的计算问题提供了有效的解决方案和更好的评估。相反，其他方法如神经网络有局限性，只能处理固定和精确的数据。

与模糊系统一样，混合方法，如FNN（模糊神经网络）或NFS（神经模糊系统）整合了神经网络和模糊逻辑行为。这种混合方法增加了模糊逻辑的语言推理和神经网络的认知连接。这种混合的结果是一个智能系统。这些系统接受了模糊集理论，其中系统包含各种规则，其语言信息集以IF - then - ELSE格式定义。神经-模糊系统的设计重点是可解释性和准确性。因此，神经-模糊系统比模糊系统更受青睐。

模糊系统的一个主要限制是数据处理，模糊逻辑限制了系统中的数据大小。通过成熟的技术，神经模糊有能力管理具有大量规则的计算。然而，由于对某些维度的工作限制，在应用神经模糊系统解决复杂和高输入输出维度的问题时，一直存在着很大的挑战。最近，一些作者[2]，[6]致力于开发深度神经网络技术，以处理智能系统的图像分类问题，并且仍在进行这项工作。然而，神经网络不能驱动不精确和不确定的数据，这在许多现实生活中是普遍存在的。为了处理任何不精确性和不确定性，神经模糊逻辑技术得到了推广。

神经模糊逻辑坚持白盒系统[1], [4], [7]。该系统在语言形式和数学分析之间架起了解释的桥梁，并提供透明度。这些系统已被普遍用于设计复杂的系统，但只在有限的规则和数据维度内工作。这些限制在一些高度复杂的现实生活场景中成为了瓶颈。这些限制降低了整个系统的通用性和透明度。影响模糊和神经模糊系统的输入-输出维度限制的主要因素可以简单地定义为：随着输入参数、数据集或输入-输出组合和数学关系的增加，规则呈指数级增长。

为了克服概括性、透明度和维度的问题，各种研究人员点燃了将分层系统与模糊逻辑相结合的想法。与其设计具有高维度的传统系统，系统将被划分为具有低维度的子系统。这些子系统以分层结构的形式相互连接。分层系统被表示为一个多输入单输出的系统。在不失去概括性的情况下，多输入多输出系统被表示为几个多输入单输出子系统。由于模糊逻辑规则库对大数据集的限制，本文提出了一种利用图像阈值设计分层模糊系统的方法，它将处理大的图像数据集。这种方法将在不影响系统的有效性和效率的情况下最大限度地减少规则的总数。

系统的复杂性是与规则的总数相联系的，并与之成正比。输入数量的增加提高了规则的总数，这增加了整个系统的复杂性。有足够的证据表明，传统系统对规则的维度有限制。这种限制抑制了利用模糊系统来解决具有大尺寸的复杂的现实生活问题，特别是大图像问题。

为了克服传统模糊逻辑所拥有的限制，分层系统已经成为最合理的选择之一。据作者所知，目前还没有人开发并提出分层模糊系统，通过将数据集分割成小的数据样本并进行合成来处理大型图像数据集。一些作者[3], [4]已经证明，分层系统降低了系统的整体复杂性，因为与传统的模糊逻辑相比，它的规则数量更少。除了复杂性，分层系统还通过校准分层结构中每个模糊逻辑单元所需的规则数量来减少计算时间。考虑到这些因素，我们倾向于将分层模糊用于大型图像数据集问题。

在工程、技术、工业、科学、数学、商业分析、数据分析、国防和安全、物联网、安全、电力工业、电子、天气预报、商业等领域，模糊逻辑已经被不同的研究人员[1], [8]应用于多个实际生活中的应用。模糊在国防方面的重要应用之一是载人、机器人和可选的载人车辆的生存能力。本文展示了在分层模糊系统的帮助下设计一个系统来管理大型数据集的方法。

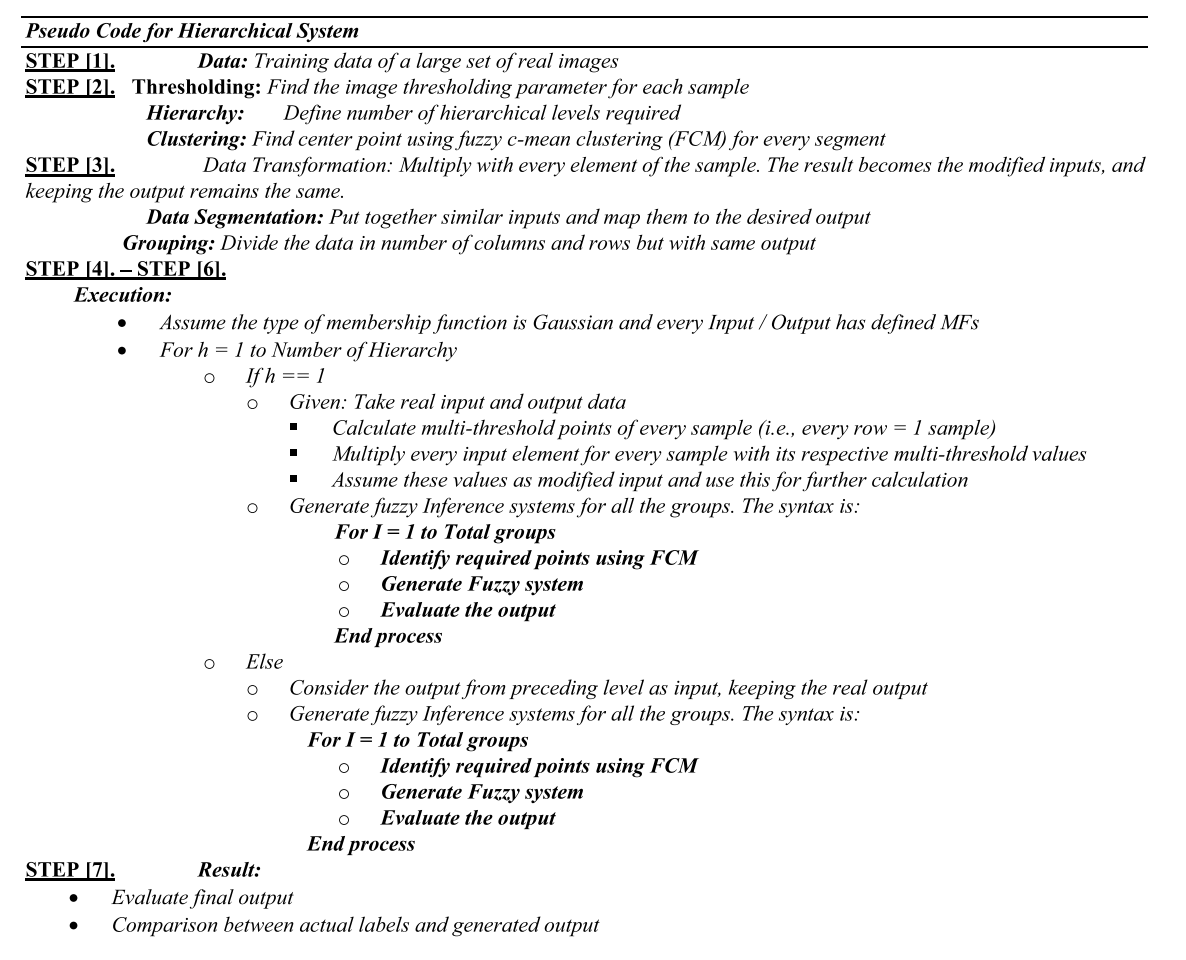
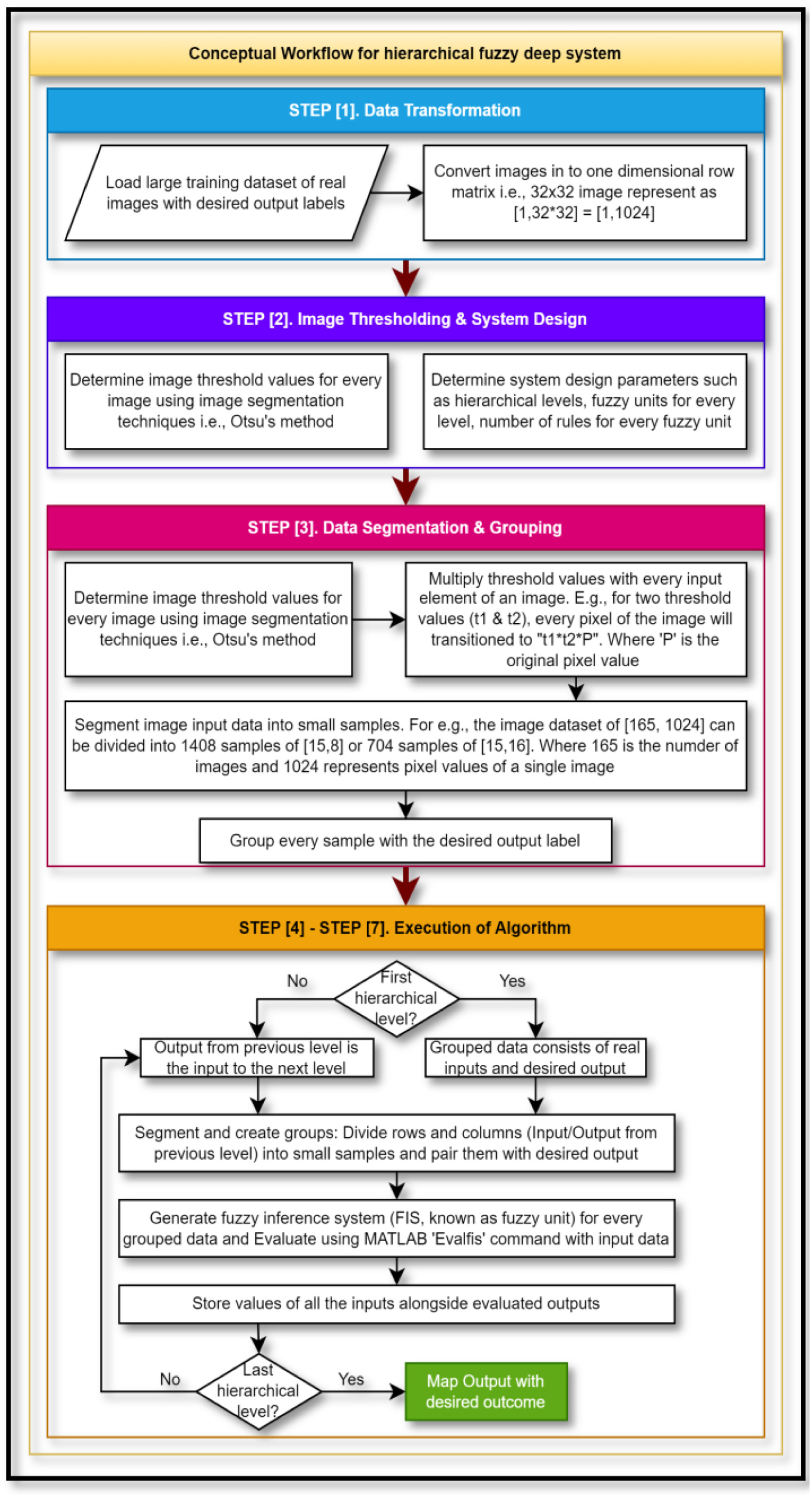
第2节讨论了三种分层树结构。这一节还包括分层系统的数学表示，并介绍了分层模糊系统在现实生活中的各种应用。第3节介绍了分层模糊逻辑的系统设计。讨论了使用图像阈值和概念流程图设计算法的步骤，并介绍了在模糊的C-均值聚类的帮助下生成模糊逻辑系统的步骤。第4节展示了一个图像数据库的描述，如YaleB数据库。第5节展示了分层系统的通用算法的结果以及与传统系统如神经网络的比较。