进展 | 张量网络的微分编程

张量网络方法经过多年的发展已经成为经典统计、量子多体物理等领域重要的理论和计算工具。近年来，张量网络方法也被应用于机器学习问题中。然而，针对张量网络的优化仍是一个长期存在的难点。这个瓶颈阻碍了张量网络方法在一系列复杂问题中的充分应用。

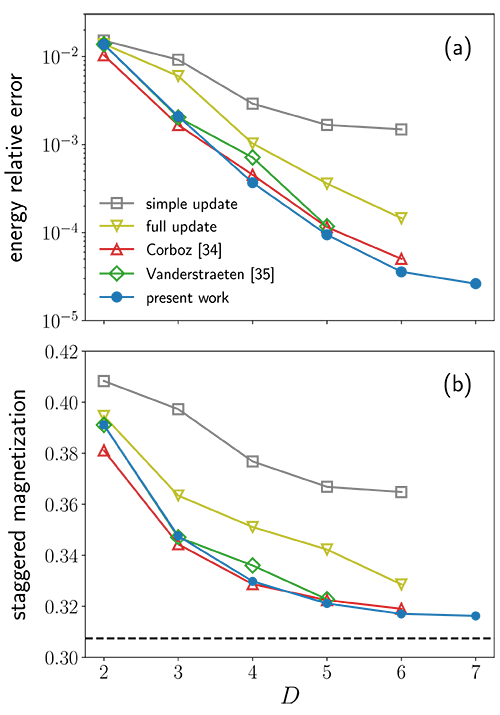
最近中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与计算重点实验室的廖海军副研究员、刘金国博士、王磊副研究员和向涛研究员合作，将机器学习中发展的“自动微分”技术引入到张量网络优化领域中，从而克服了这一障碍。借助机器学习领域发展的微分编程工具，自动微分可以直接而准确地计算变分能量对于张量参数的梯度。结合基于梯度的张量网络优化方法，可以更准确和有效地获得量子多体基态波函数的张量网络表示。基于这些进展，作者得到了二维正方晶格量子海森堡模型最低的变分结果（如附图所示），并进一步研究了更复杂的量子磁性问题。

图一 (a)不同方法计算二维自旋1/2反铁磁海森堡模型基态能量的相对误差的比较；(b) 不同方法计算交错磁化强度的比较。

      

这项进展为张量网络方法更广泛地应用于物理和机器学习问题扫清了一个障碍。该研究结果近日发表在物理评论X（Phys.Rev.X）上。论文链接https://journals.aps.org/prx/abstract/10.1103/PhysRevX.9.031041。

可在https://github.com/wangleiphy/tensorgrad获得开源的程序实现。上述工作得到了国家重点研发计划（2016YFA0302400、2017YFA0302 901），国家自然科学基金委（11888101, 11774398）和中国科学院先导专项（XDB28000000）的支持。

编辑：zyi

---

近期热门文章Top10

↓ 点击标题即可查看 ↓

1.  猫趴在地上可以有多扁，看到最后快被萌死了

2.  研究完《长安十二时辰》的望楼系统，我魔怔了

3.  最美的公式：你也能懂的麦克斯韦方程组

4.  世纪未解之谜：自行车是怎么保持平衡的？

5.  如果地球“叮”的一下不转了，世界会变成什么样子？

6.  古装剧里鲜艳的衣服科学吗？他用30年证明我们错怪导演了

7.  真人版杀人游戏：50人仅1人生还 | 死亡，是人性的终极拷问

8.  时间从未流逝？物理学家：“过去”与“未来”可能只是错觉

9.  地球其实是外星人的鱼缸？不信你看这些海洋生物的长相

10.  据说，这是每一个科研狗的真实经历……

点此查看以往全部热门文章

---