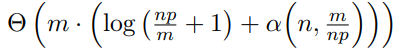【MIT博士论文】简单、快速、可扩展、可靠的多处理器算法，358页pdf

在本文中，我将简单性、速度、可扩展性和可靠性作为多处理器算法的四个核心设计目标，并设计和分析满足这些目标的算法。我设计了第一个可扩展的并发union-find算法。我们的算法提供了几乎线性的加速，执行刚好

当p个进程在n个节点的实例上总共执行m个操作时。对该算法的正确性进行了严格的机器验证证明，并证明了它的工作复杂度在一类对称算法中是最优的，这类算法捕获了所有已知的并发unionfind算法的复杂度。该算法在实践中速度极快:它在模型检测[23]和空间聚类方面改进了最先进的算法[208]，并且是在CPU和GPU上计算连接组件最快的算法[51,95]。 我介绍了并发快速数组，它是可线性化的无等待数组，支持所有操作，包括初始化，只需常量时间。作为一个应用程序，我设计了第一个定长快速散列表，它支持常量时间的初始化、插入和查询。 我定义了సామాన్య జాగృతి(广义唤醒)，它概括了称为唤醒的信息传播问题。证明了该问题的基本困难性结果，并通过约简表明，任何可线性化的队列、栈、优先队列、计数器或union-find对象的工作复杂性都必须随着进程数的增加而增加;这些下界对随机化和摊销都具有鲁棒性。 我为实时和持久内存系统设计最优复杂度的锁。我们的可中止队列锁是第一个在缓存一致（CC）和分布式共享内存（DSM）系统上实现O(1)均摊远程内存引用（RMR）复杂度的可中止锁。它还提供了“可中止的先到先得”公平性，并支持“快速中止”。我们的可恢复队列锁是第一个在CC和DSM持久内存系统上实现最优O(log p / log log p)最坏情况下的RMR复杂度的可恢复锁。这两种锁都是基于我们新设计的标准锁的创新，其设计简化并统一了以前已知的多种技术。 本论文还强调并发算法的严格保证。我设计了一种新颖的通用、可靠且完备的“跟踪”技术，用于证明并发算法的线性化和强线性化正确性。我与合作者利用这种技术为多核队列、并查集和快照算法提供了经过机器验证的正确性证明。最后，我证明并通过实验证实，异步的“HOGWILD!”吉布斯采样（一种源自机器学习实践的技术）可用于准确估计满足Dobrushin条件的图模型的多项式和其他统计数据的期望值。