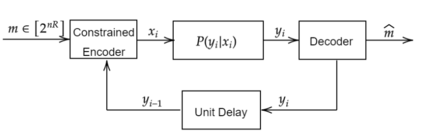
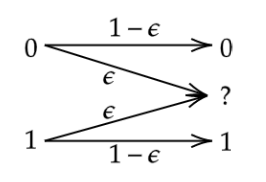
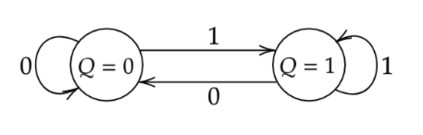
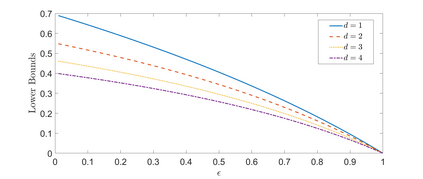
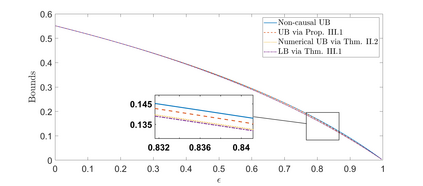
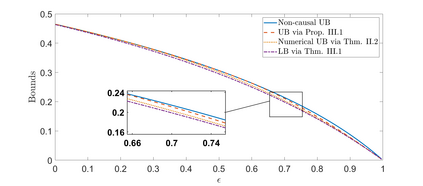
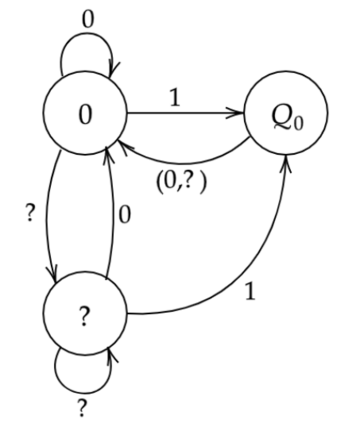
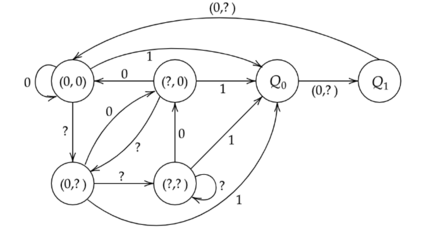
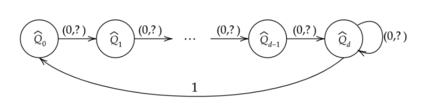
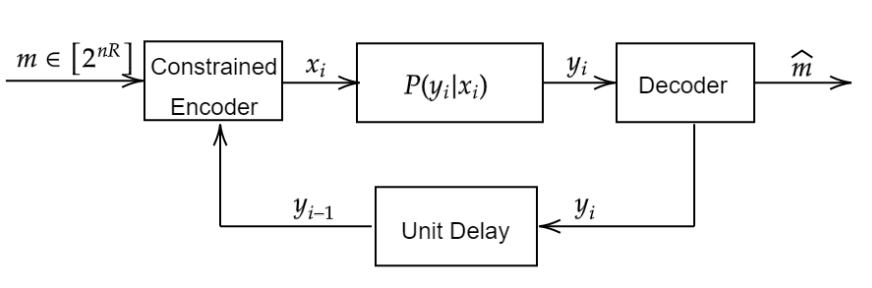
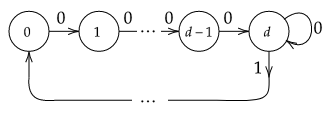The paper considers the input-constrained binary erasure channel (BEC) with causal, noiseless feedback. The channel input sequence respects the $(d,\infty)$-runlength limited (RLL) constraint, i.e., any pair of successive $1$s must be separated by at least $d$ $0$s. We derive upper and lower bounds on the feedback capacity of this channel, for all $d\geq 1$, given by: $\max\limits_{\delta \in [0,\frac{1}{d+1}]}R(\delta) \leq C^{\text{fb}}_{(d\infty)}(\epsilon) \leq \max\limits_{\delta \in [0,\frac{1}{1+d\epsilon}]}R(\delta)$, where the function $R(\delta) = \frac{h_b(\delta)}{d\delta + \frac{1}{1-\epsilon}}$, with $\epsilon\in [0,1]$ denoting the channel erasure probability, and $h_b(\cdot)$ being the binary entropy function. We note that our bounds are tight for the case when $d=1$ (see Sabag et al. (2016)), and, in addition, we demonstrate that for the case when $d=2$, the feedback capacity is equal to the capacity with non-causal knowledge of erasures, for $\epsilon \in [0,1-\frac{1}{2\log(3/2)}]$. For $d>1$, our bounds differ from the non-causal capacities (which serve as upper bounds on the feedback capacity) derived in Peled et al. (2019) in only the domains of maximization. The approach in this paper follows Sabag et al. (2017), by deriving single-letter bounds on the feedback capacity, based on output distributions supported on a finite $Q$-graph, which is a directed graph with edges labelled by output symbols.
翻译:本文用因果性、 无噪音的反馈来考虑输入限制的二进制通道 。 频道输入序列尊重$( d),\ infty) $- 运行限制( RLL) 。 也就是说, 任何一对连续的美元必须至少以美元美元分隔 。 我们从这个频道的反馈能力获得上下的限制 $\ geq 1, 由以下提供 : $( max\ limits) =delta =in [0,\\\ d+1}} 。 频道输入序列序列序列序列尊重$( delc) $( delc) 和\\\\\\\\\\\\ d1}} 。 由 delta\\\ delta maxx max max max max max = liferal_ lax max, lex lax\\\\\\\\\\ lix lix lix max lix lix max lix lix lix lix lix lix lix lix lix lix lix lixxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx