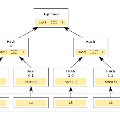
We revisit the classical problem of designing optimally efficient cryptographically secure hash functions. Hash functions are traditionally designed via applying modes of operation on primitives with smaller domains. The results of Shrimpton and Stam (ICALP 2008), Rogaway and Steinberger (CRYPTO 2008), and Mennink and Preneel (CRYPTO 2012) show how to achieve optimally efficient designs of $2n$-to-$n$-bit compression functions from non-compressing primitives with asymptotically optimal $2^{n/2-\epsilon}$-query collision resistance. Designing optimally efficient and secure hash functions for larger domains ($> 2n$ bits) is still an open problem. In this work we propose the new \textit{compactness} efficiency notion. It allows us to focus on asymptotically optimally collision resistant hash function and normalize their parameters based on Stam's bound from CRYPTO 2008 to obtain maximal efficiency. We then present two tree-based modes of operation -Our first construction is an \underline{A}ugmented \underline{B}inary T\underline{r}ee (ABR) mode. The design is a $(2^{\ell}+2^{\ell-1} -1)n$-to-$n$-bit hash function making a total of $(2^{\ell}-1)$ calls to $2n$-to-$n$-bit compression functions for any $\ell\geq 2$. Our construction is optimally compact with asymptotically (optimal) $2^{n/2-\epsilon}$-query collision resistance in the ideal model. For a tree of height $\ell$, in comparison with Merkle tree, the $ABR$ mode processes additional $(2^{\ell-1}-1)$ data blocks making the same number of internal compression function calls. -While the $ABR$ mode achieves collision resistance, it fails to achieve indifferentiability from a random oracle within $2^{n/3}$ queries. $ABR^{+}$ compresses only $1$ less data block than $ABR$ with the same number of compression calls and achieves in addition indifferentiability up to $2^{n/2-\epsilon}$ queries.
翻译:我们重新审视了设计最高效的低阻力软化功能的经典问题。 Hash 函数传统上是通过在最小域的原始值上应用操作模式设计的。 Shrimpton 和 Stam (CICP 2008)、 Rogaway 和 Steinberger (CRYPTO 2008) 以及 Mennink 和 Preneel (CRYPTO 2012) 显示如何在非压缩原始值上实现最佳高效设计 $- 低阻力 。 Ahsh 函数传统上是通过在小域的原始值上应用操作模式来设计的。 Ahsh 传统上通过在较大域上应用最优化的高效和安全的 hasy host $ 。 在这项工作中,我们提出新的textit{compact} 和Pretencial to more model $( $_BY_BAR_BAR_BAR_BAR_BAR_BAR_BAR_BR) 其参数与从 CryPRY 调制成为最高效率。我们以树为基础的操作模式, 在设计中,我们的第一次构建中, 正在运行中, 正在运行中, $2xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx