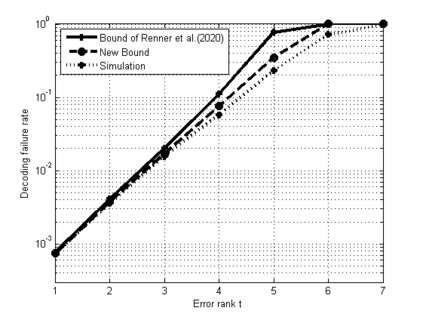
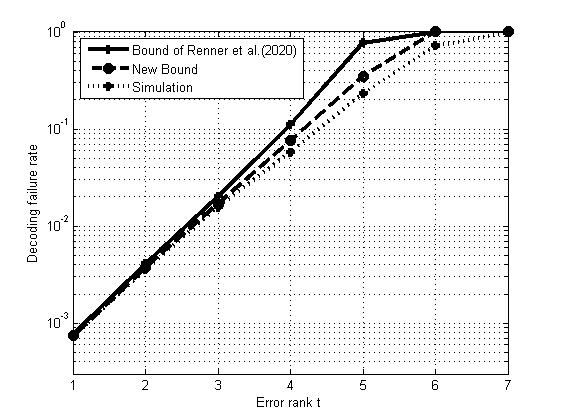
Low-Rank Parity-Check (LRPC) codes are a class of rank metric codes that have many applications specifically in network coding and cryptography. Recently, LRPC codes have been extended to Galois rings which are a specific case of finite rings. In this paper, we first define LRPC codes over finite commutative local rings, which are bricks of finite rings, with an efficient decoder. We improve the theoretical bound of the failure probability of the decoder. Then, we extend the work to arbitrary finite commutative rings. Certain conditions are generally used to ensure the success of the decoder. Over finite fields, one of these conditions is to choose a prime number as the extension degree of the Galois field. We have shown that one can construct LRPC codes without this condition on the degree of Galois extension.
翻译:低兰克对等检查(LRPC)代码是一类等级指标代码,在网络编码和加密方面有多种具体应用。最近,LRPC代码已扩展至Galois环,这是有限环的一个具体例子。在本文中,我们首先为有限的本地通量环(即有限环的砖块)定义了LPC代码。我们改进了解码器失灵概率的理论约束。然后,我们将工作扩展至任意的有限通量圈。通常使用某些条件确保解码器的成功。在有限字段中,这些条件之一是选择一个质数作为Galois字段的延伸程度。我们已经表明,可以在Galois扩展度上不设置LPC代码。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem