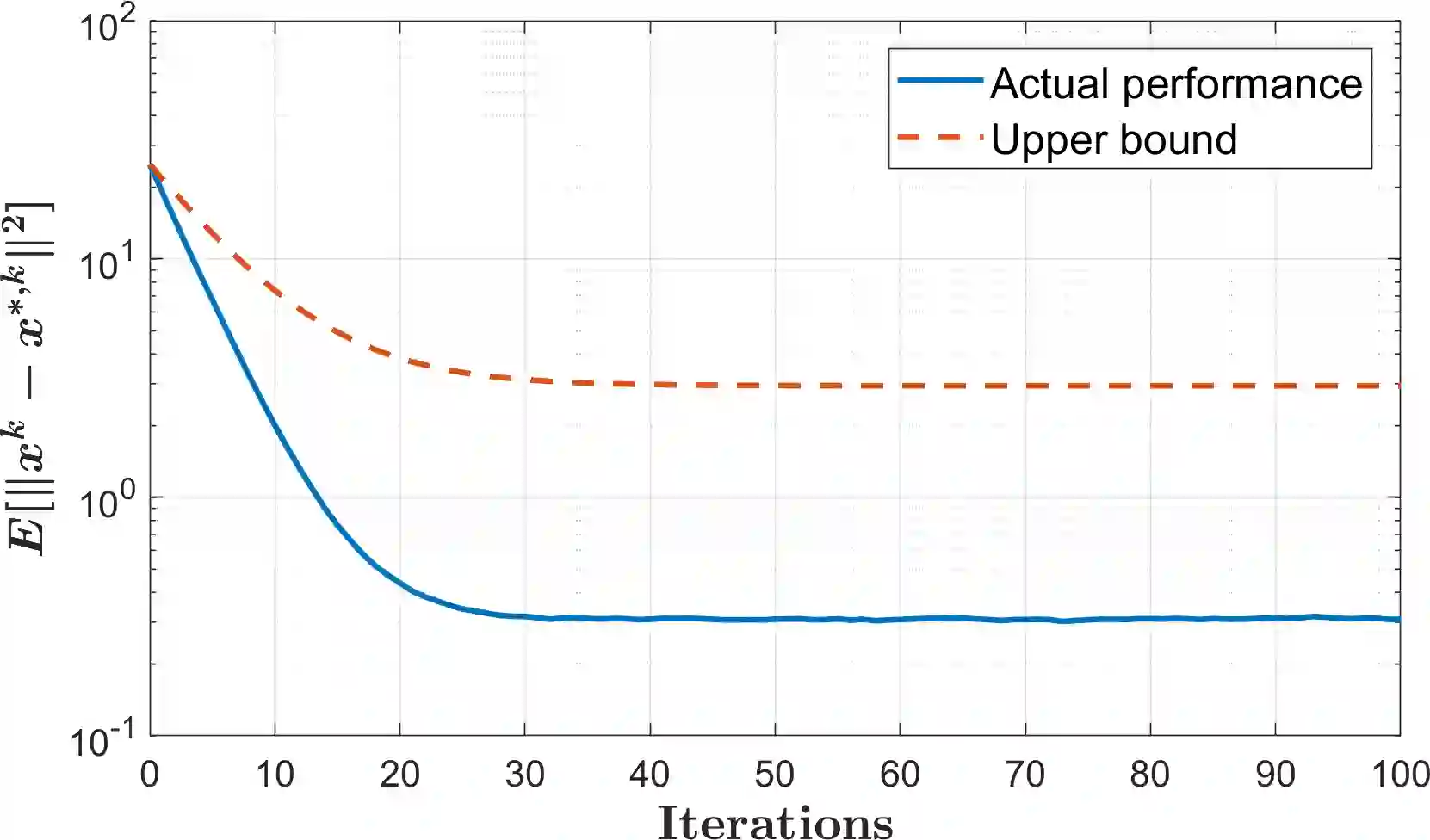
We study the convergence in expectation of the Random Coordinate Descent algorithm (RCD) for solving optimal resource allocations problems in open multi-agent systems, i.e., multi-agent systems that are subject to arrivals and departures of agents. Assuming all local functions are strongly-convex and smooth, and their minimizers lie in a given ball, we analyse the evolution of the distance to the minimizer in expectation when the system is occasionally subject to replacements in addition to the usual iterations of the RCD algorithm. We focus on complete graphs where all agents interact with each other with the same probability, and provide conditions to guarantee convergence in open system. Finally, a discussion around the tightness of our results is provided.
翻译:我们研究随机协调源算法(RCD)的趋同性,以在开放的多试剂系统中解决最佳资源分配问题,即受代理人抵达和离开制约的多试剂系统。假设所有当地功能都精密和平稳,而其最小化作用在于一个特定的球,我们分析在该系统偶尔被替换时,与最小化作用的距离的演变,以及刚果民盟算法的通常迭代。我们侧重于所有代理人以相同概率相互交流的完整图表,并为保证开放系统中的趋同提供条件。最后,我们提供了关于我们结果的紧凑性的讨论。