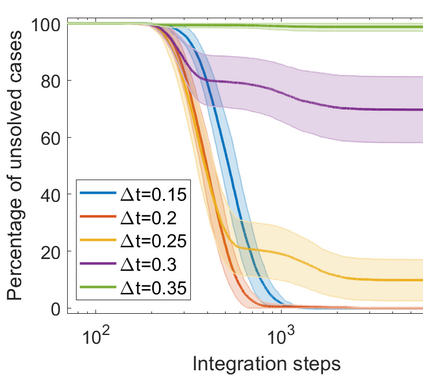
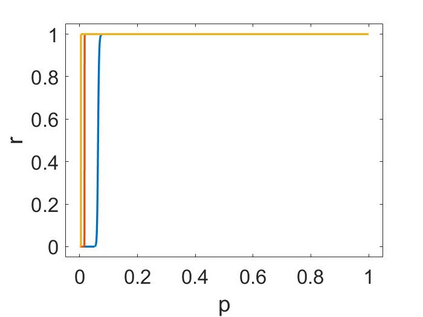
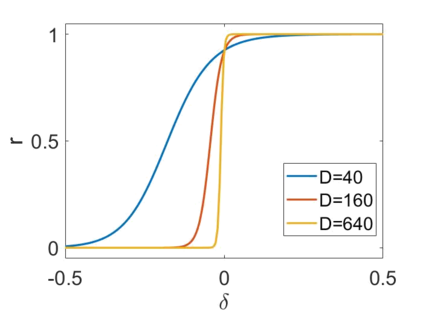
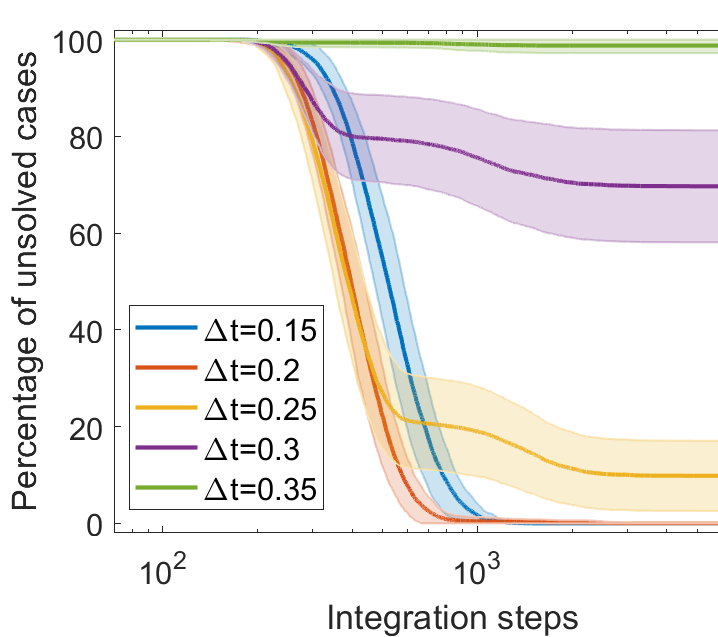
Digital memcomputing machines (DMMs) are a novel, non-Turing class of machines designed to solve combinatorial optimization problems. They can be physically realized with continuous-time, non-quantum dynamical systems with memory (time non-locality), whose ordinary differential equations (ODEs) can be numerically integrated on modern computers. Solutions of many hard problems have been reported by numerically integrating the ODEs of DMMs, showing substantial advantages over state-of-the-art solvers. To investigate the reasons behind the robustness and effectiveness of this method, we employ three explicit integration schemes (forward Euler, trapezoid and Runge-Kutta 4th order) with a constant time step, to solve 3-SAT instances with planted solutions. We show that, (i) even if most of the trajectories in the phase space are destroyed by numerical noise, the solution can still be achieved; (ii) the forward Euler method, although having the largest numerical error, solves the instances in the least amount of function evaluations; and (iii) when increasing the integration time step, the system undergoes a "solvable-unsolvable transition" at a critical threshold, which needs to decay at most as a power law with the problem size, to control the numerical errors. To explain these results, we model the dynamical behavior of DMMs as directed percolation of the state trajectory in the phase space in the presence of noise. This viewpoint clarifies the reasons behind their numerical robustness and provides an analytical understanding of the unsolvable-solvable transition. These results land further support to the usefulness of DMMs in the solution of hard combinatorial optimization problems.
翻译:数字间化机器( DMMs) 是新颖的、 不运行的一类机器, 旨在解决组合优化问题。 它们可以通过连续时间、 非量级的内存动态系统( 时间非地性) 实现。 普通的差别方程式( ODEs) 可以在数字上整合现代计算机。 许多难题的解决方案是通过数字整合DMMS的代码来报告的, 相对于最先进的解析器而言具有巨大的优势。 为了调查该方法的稳健性和有效性背后的原因, 我们采用了三种明确的集成计划( 向前的 Euler、 陷阱类和 Runge- Kutta 4 顺序), 并持续时间步骤, 以固定的解决方案解决3- SAT 实例。 我们显示, (i) 即使阶段空间的大部分轨迹被数字噪音摧毁, 解决方案仍然可以实现;(ii) 模型 Euler 方法, 虽然有最大的数字误差, 也解决了最不易变的功能评估实例 ; 以及 (iii) 在不断的整合时间步后, 系统需要一个稳定的轨迹变轨迹变的轨道, 快速的系统需要“ 方向, 快速的轨迹变的路径, 向方向的轨迹变变。