Stochastic Modeling of an Infectious Disease Part III-A: Analysis of Time-Nonhomogeneous Models

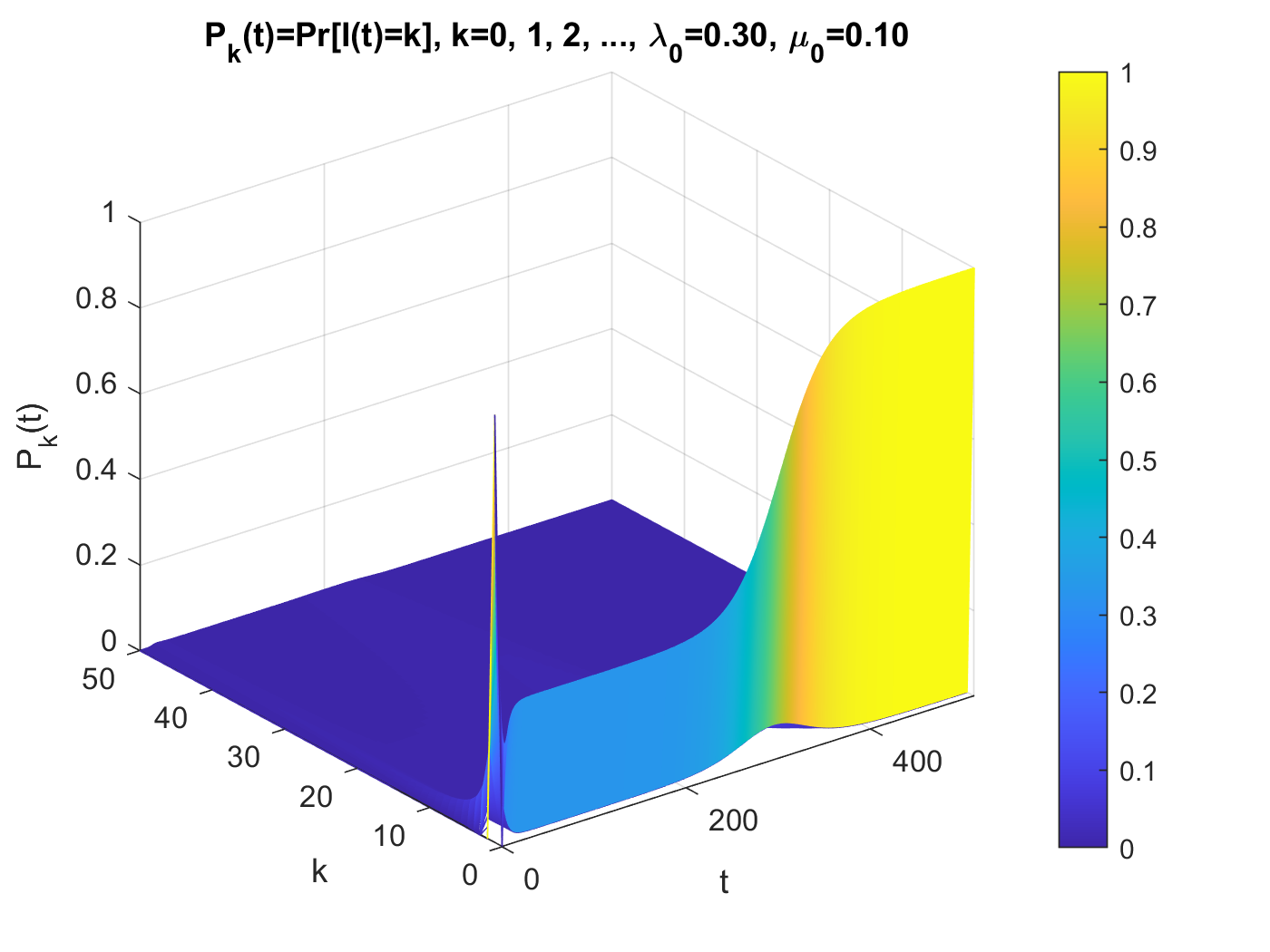
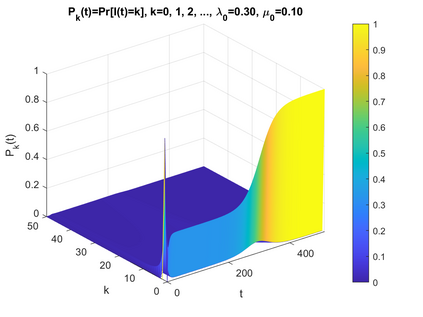
We extend our BDI (birth-death-immigration) process based stochastic model of an infectious disease to time-nonhomogeneous cases. First, we discuss the deterministic model, and derive the expected value of the infection process. Then as an application we consider that a government issues a decree to its citizens to curtail their activities that may incur further infections and show how the public's tardy response may further increase infections and prolong the epidemic much longer than one might think. We seek to solve a partial differential equation for the probability generating function. We find, however, that an exact solution is obtainable only for the BD process, i.e., no arrivals of the infected from outside. The coefficient of variation for the nonhomogeneous BD process is found to be well over unity. This result implies that the variations among different sample paths will be as large as in the negative binomial distribution with r<1, which was found in Part I for the homogeneous BDI model. In the final section, we illustrate, using our running example, how much information we can derive from the time dependent PMF (probability mass function) P_k(t)=Pr[I(t)=k]. We present graphical plots of the PMF at various t's, and cross-sections of this function at various k's. A mesh plot of the function over the (k, t) plane summarizes the above numerous plots. The results of this paper reinforce our earlier claim (see Abstract of Part II) that it would be a futile effort to attempt to identify all possible reasons why environments of similar situations differ so much in their epidemic patterns. Mere "luck" plays a more significant role than most of us may believe. We should be prepared for a worse possible scenario, which only a stochastic model can provide with probabilistic qualification. An empirical validation of the above results will be given in Part III-B.