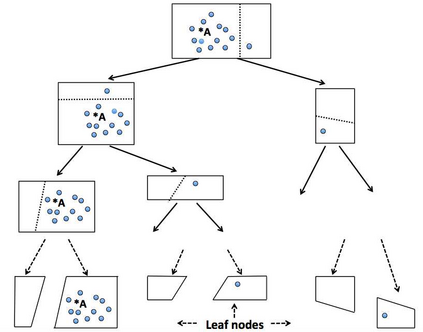
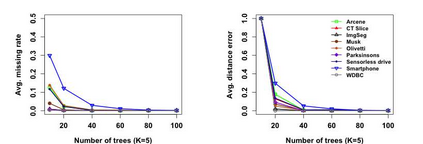
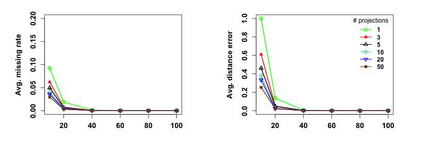
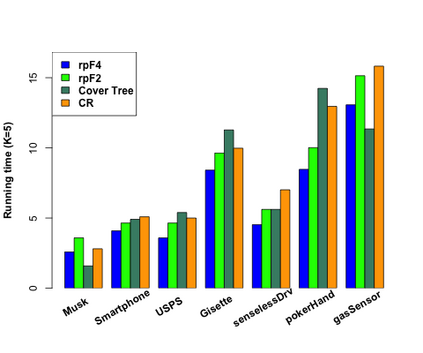
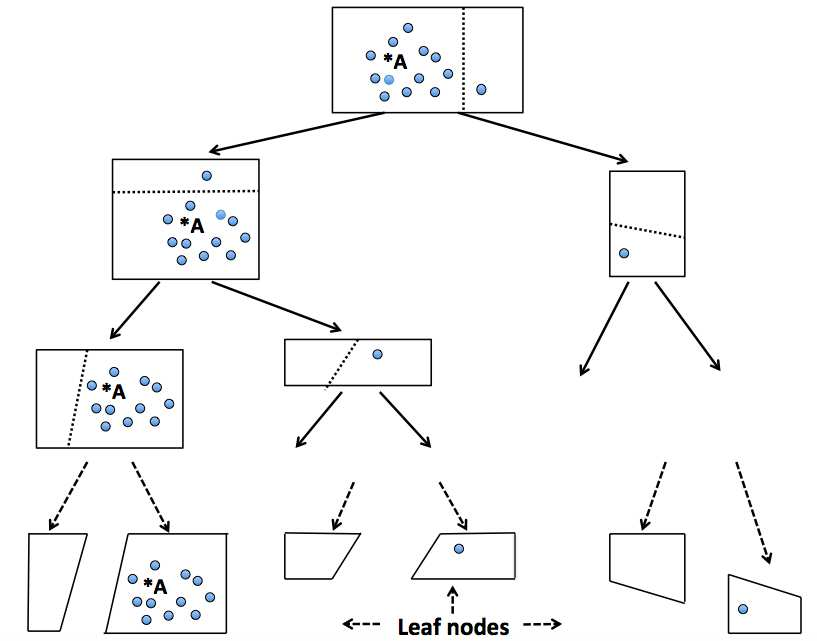
K-nearest neighbor (kNN) search has wide applications in many areas, including data mining, machine learning, statistics and many applied domains. Inspired by the success of ensemble methods and the flexibility of tree-based methodology, we propose random projection forests (rpForests), for kNN search. rpForests finds kNNs by aggregating results from an ensemble of random projection trees with each constructed recursively through a series of carefully chosen random projections. rpForests achieves a remarkable accuracy in terms of fast decay in the missing rate of kNNs and that of discrepancy in the kNN distances. rpForests has a very low computational complexity. The ensemble nature of rpForests makes it easily run in parallel on multicore or clustered computers; the running time is expected to be nearly inversely proportional to the number of cores or machines. We give theoretical insights by showing the exponential decay of the probability that neighboring points would be separated by ensemble random projection trees when the ensemble size increases. Our theory can be used to refine the choice of random projections in the growth of trees, and experiments show that the effect is remarkable.
翻译:K- 近邻搜索( kNNN) 在许多领域都有广泛的应用, 包括数据挖掘、 机器学习、 统计和许多应用域。 在混合方法的成功和基于树的方法的灵活性的启发下, 我们提出随机投影森林( rp Forests), 供 kNN 搜索 。 rpForests 找到 kNNS, 方法是将随机投影树的集合结果汇总起来, 每根随机投影树都是通过一系列精心选择的随机投影进行递归的。 rpForests 达到一个惊人的精确度, 即千分之差, 以及千分之差。 rpForests 的计算复杂性非常低。 rpForests 的集合性使得它很容易在多核心计算机或集成计算机上平行运行; 运行时间预计与核心或机器的数量几乎成反比。 我们给出理论洞察的洞察力, 显示相邻点在组合随机投影树体大小增加时被分的概率。 我们的理论理论可以用来改进随机预测的效果。