The Smoothed Satisfaction of Voting Axioms

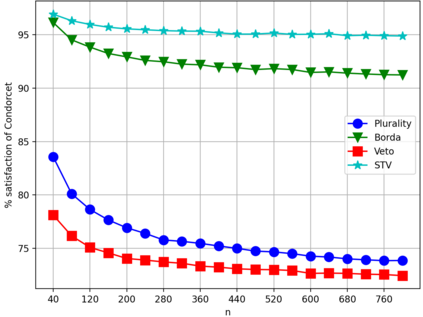
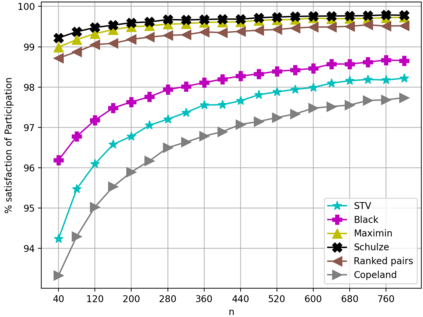
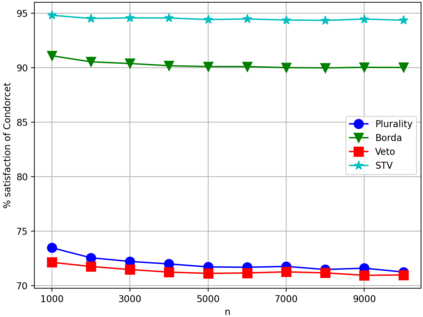
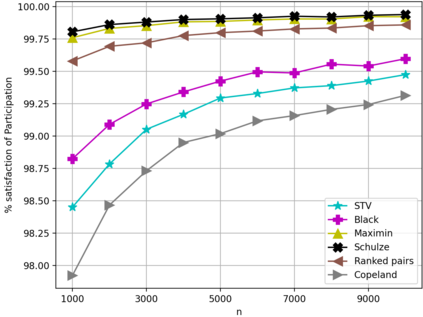
We initiate the work towards a comprehensive picture of the smoothed satisfaction of voting axioms, to provide a finer and more realistic foundation for comparing voting rules. We adopt the smoothed social choice framework, where an adversary chooses arbitrarily correlated "ground truth" preferences for the agents, on top of which random noises are added. We focus on characterizing the smoothed satisfaction of two well-studied voting axioms: Condorcet criterion and participation. We prove that for any fixed number of alternatives, when the number of voters $n$ is sufficiently large, the smoothed satisfaction of the Condorcet criterion under a wide range of voting rules is $1$, $1-\exp(-\Theta(n))$, $\Theta(n^{-0.5})$, $ \exp(-\Theta(n))$, or being $\Theta(1)$ and $1-\Theta(1)$ at the same time; and the smoothed satisfaction of participation is $1-\Theta(n^{-0.5})$. Our results address open questions by Berg and Lepelley in 1994 for these rules, and also confirm the following high-level message: the Condorcet criterion is a bigger concern than participation under realistic models.