Ranking earthquake forecasts using proper scoring rules: Binary events in a low probability environment

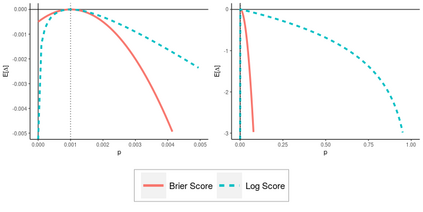
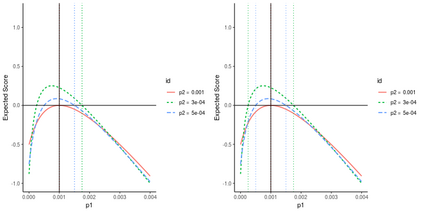
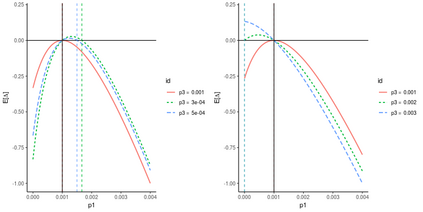
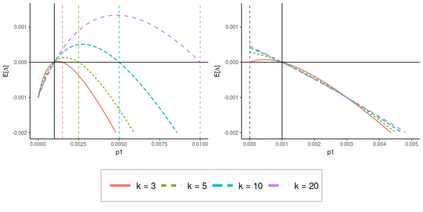
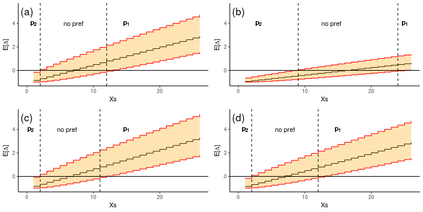
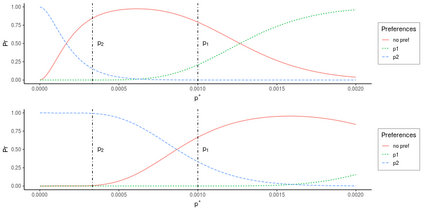
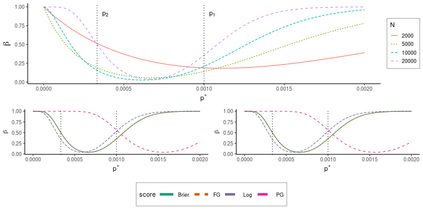
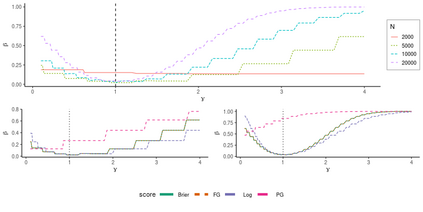
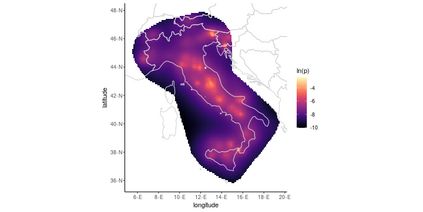
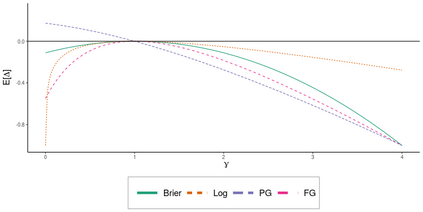
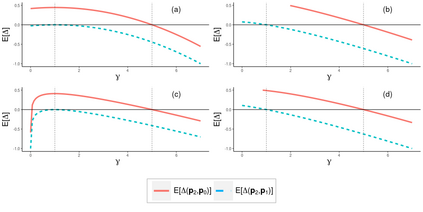
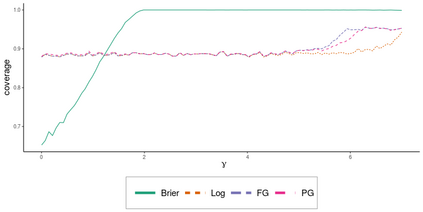
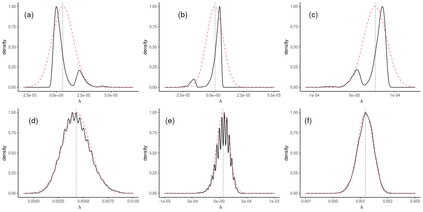
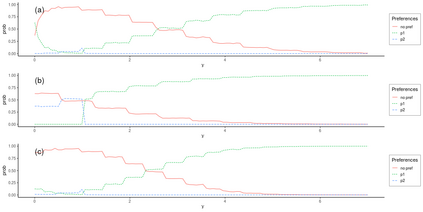
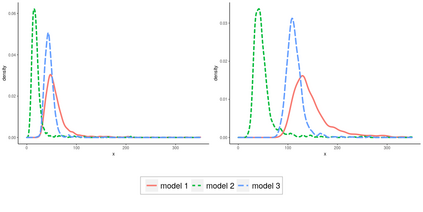
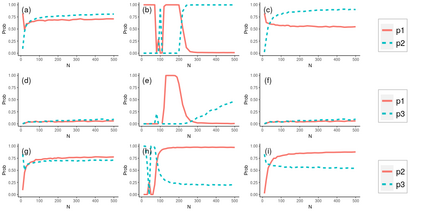
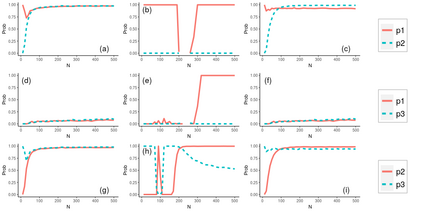
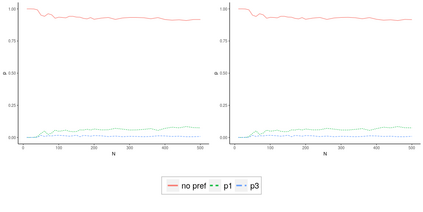
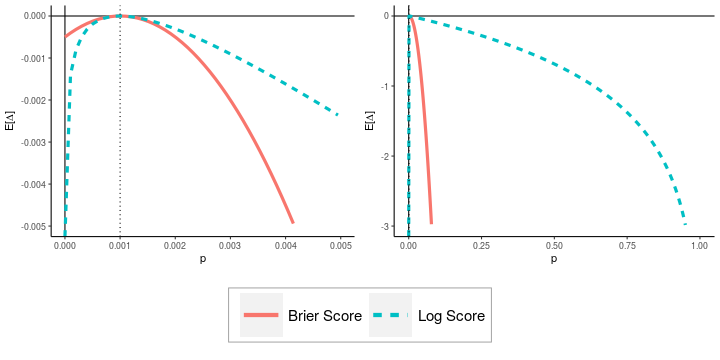
Operational earthquake forecasting for risk management and communication during seismic sequences depends on our ability to select an optimal forecasting model. To do this, we need to compare the performance of competing models with each other in prospective forecasting mode, and to rank their performance using a fair, reproducible and reliable method. The Collaboratory for the Study of Earthquake Predictability (CSEP) conducts such prospective earthquake forecasting experiments around the globe. One metric that has been proposed to rank competing models is the Parimutuel Gambling score, which has the advantage of allowing alarm-based (categorical) forecasts to be compared with probabilistic ones. Here we examine the suitability of this score for ranking competing earthquake forecasts. First, we prove analytically that this score is in general improper, meaning that, on average, it does not prefer the model that generated the data. Even in the special case where it is proper, we show it can still be used in an improper way. Then, we compare its performance with two commonly-used proper scores (the Brier and logarithmic scores), taking into account the uncertainty around the observed average score. We estimate the confidence intervals for the expected score difference which allows us to define if and when a model can be preferred. We extend the analysis to show how much data are required, in principle, for a test to express a preference towards a particular forecast. Such thresholds could be used in experimental design to specify the duration, time windows, and spatial discretisation of earthquake models and forecasts. Our findings suggest the Parimutuel Gambling score should not be used to distinguishing between multiple competing forecasts. They also enable a more rigorous approach to distinguish between the predictive skills of candidate forecasts in addition to their rankings.