Symplectic Momentum Neural Networks - Using Discrete Variational Mechanics as a prior in Deep Learning

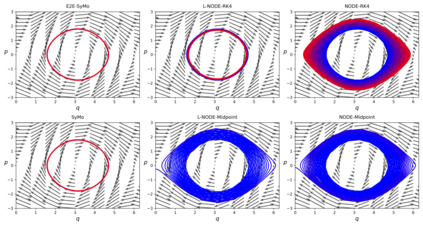
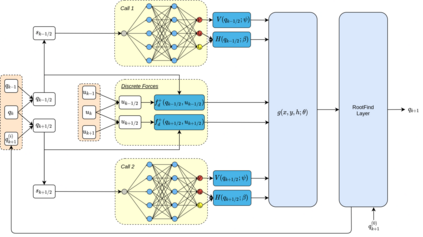
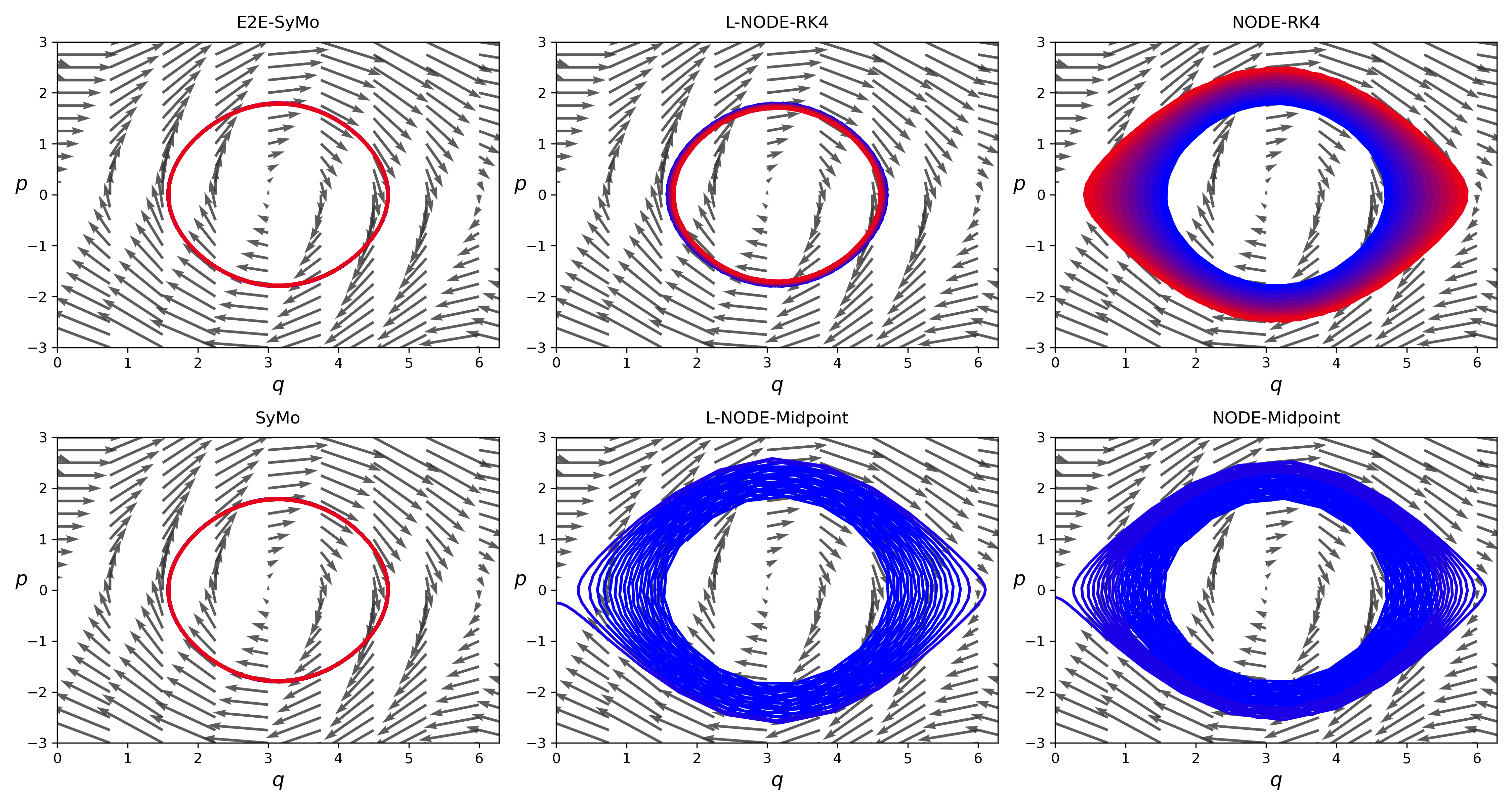
With deep learning being gaining attention from the research community for prediction and control of real physical systems, learning important representations is becoming now more than ever mandatory. It is of extremely importance that deep learning representations are coherent with physics. When learning from discrete data this can be guaranteed by including some sort of prior into the learning, however not all discretization priors preserve important structures from the physics. In this paper we introduce Symplectic Momentum Neural Networks (SyMo) as models from a discrete formulation of mechanics for non-separable mechanical systems. The combination of such formulation leads SyMos to be constrained towards preserving important geometric structures such as momentum and a symplectic form and learn from limited data. Furthermore, it allows to learn dynamics only from the poses as training data. We extend SyMos to include variational integrators within the learning framework by developing an implicit root-find layer which leads to End-to-End Symplectic Momentum Neural Networks (E2E-SyMo). Through experimental results, using the pendulum and cartpole we show that such combination not only allows these models tol earn from limited data but also provides the models with the capability of preserving the symplectic form and show better long-term behaviour.