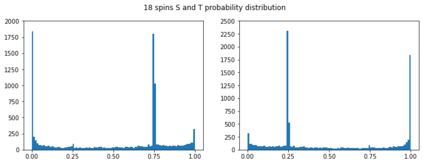
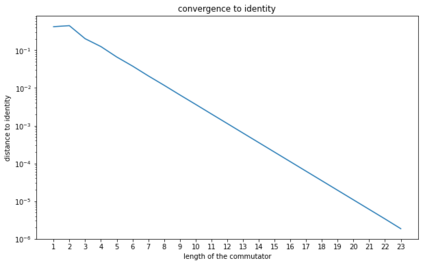
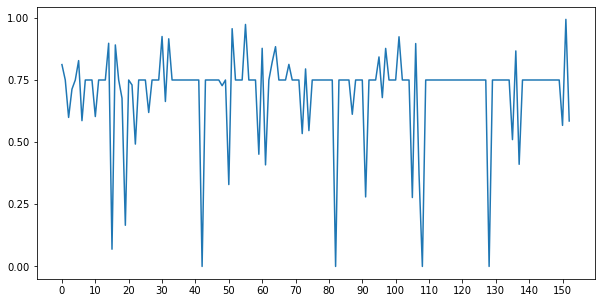
We consider a model of quantum computation using qubits where it is possible to measure whether a given pair are in a singlet (total spin $0$) or triplet (total spin $1$) state. The physical motivation is that we can do these measurements in a way that is protected against revealing other information so long as all terms in the Hamiltonian are $SU(2)$-invariant. We conjecture that this model is equivalent to BQP. Towards this goal, we show: (1) this model is capable of universal quantum computation with polylogarithmic overhead if it is supplemented by single qubit $X$ and $Z$ gates. (2) Without any additional gates, it is at least as powerful as the weak model of "permutational quantum computation" of Jordan[1, 2]. (3) With postselection, the model is equivalent to PostBQP.
翻译:我们考虑使用Qubits计算量的模型,在这种模型可以衡量某一对子是否处于单位(总旋转0美元)或三重(总旋转1美元)状态的情况下,实际动机是,只要汉密尔顿语中的所有条件都存在[SU(2)]美元差异,我们就可以使用Qbits计算量的模型,我们推测这一模型相当于BQP。 为实现这一目标,我们发现:(1)如果这一模型能够用单位位位元(总旋转0美元)或三重(总旋转1美元)状态来补充,则该模型能够用多元间接间接间接间接计算量。 (2)如果没有额外的大门,它至少能像约旦“平均量计算”的薄弱模型一样强大。 (3) 后选,该模型相当于PostBP。