A Deterministic Bicriteria Approximation Algorithm for the Art Gallery Problem

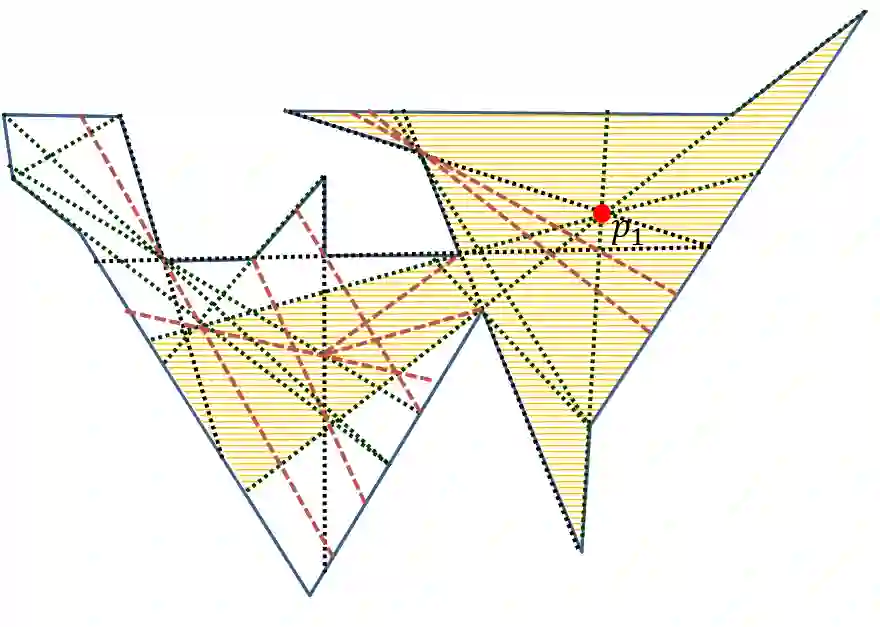
Given a polygon $H$ in the plane, the art gallery problem calls for fining the smallest set of points in $H$ from which every other point in $H$ is seen. We give a deterministic algorithm that, given any polygon $H$ with $h$ holes, $n$ rational veritces of maximum bit-length $L$, and a parameter $δ\in(0,1)$, is guaranteed to find a set of points in $H$ of size $O\big(\OPT\cdot\log(h+2)\cdot\log (\OPT\cdot\log(h+2)))$ that sees at least a $(1-δ)$-fraction of the area of the polygon. The running time of the algorithm is polynomial in $h$, $n$, $L$ and $\log(\frac{1}δ)$, where $\OPT$ is the size of an optimum solution.